Dynamic Programming

Dynamic programming.

Dynamic Programming

Dynamic Programming

Identify whether a recursive algorithm can be rewritten using DP.
Explain how unique paths can be counted using recursion and DP.
Explain how a min-cost seam can be found using recursion and DP.

Graph data structures (like adjacency lists) and graph algorithms (like Dijkstra’s algorithm) provided reusable abstractions for addressing many kinds of problems. Reduction refers to exactly this problem solving approach: modifying the input data to a problem so that an existing algorithm can solve it.

Reduction

A problem-solving approach that works by reframing problem A in terms of another problem B:

Preprocess. Take the original input to A and modify it so that it works as an input to B.
Run a standard algorithm for problem B on this input, returning some output.
Postprocess. Modify this output so that it can be understood as the expected output for A.

We’ve actually already seen several examples of reduction algorithms that we just didn’t call “reductions” at the time. For example, in the project, we learned that seam finding reduces to single-pair shortest paths:

First, we constructed a PixelGraph from your input Picture.
Then, we ran a shortest paths algorithm, returning the shortest path as a list of nodes.
Finally, we extracted the y-index of each node representing the pixels in the seam to remove.

Reduction algorithms are a very common approach to solving problems in computer science. They also work without graphs as input or context. Remember dup1 and dup2 from the first week of the course? dup1 detects duplicates in an array by checking every pair of items in quadratic time. dup2 detects duplicates in a sorted array in just linear time. The problem of duplicate detection reduces to sorting because we can just sort the array and then run dup2, which can be much faster than dup1. Inventing faster sorting algorithms doesn’t just mean faster sorting, but faster everything because so many problems reduce to or otherwise depend on sorting.

Eric Allender summarizes the importance of this insight:¹

If A is efficiently reducible to B, and B is efficiently reducible to A, then in a very meaningful sense, A and B are “equivalent”—they are merely two different ways of looking at the same problem. Thus instead of infinitely many different apparently unrelated computational problems, one can deal instead with a much smaller number of classes of equivalent problems […] Nothing had prepared the computing community for the shocking insight that there are really just a handful of fundamentally different computational problems that people want to solve.

Although reductions provide a powerful way to define classes of equivalent computational problems, they don’t necessarily lead to the most experimentally-efficient solutions. The seam finding reduction to single-pair shortest paths will be limited by the runtime for shortest paths algorithms like Dijkstra’s algorithm. In practice, algorithm designers apply algorithm design paradigms like dynamic programming to develop more efficient solutions when greater efficiency is necessary.

Fibonacci sequence case study

The Fibonacci Sequence is a series of numbers in which each number is the sum of the two preceding numbers, starting with 0 and 1. We can represent this rule as a recurrence: F(N) = F(N - 1) + F(N - 2) with the base cases F(0) = 0 and F(1) = 1.

By converting this recurrence into a program, we can compute the N^th Fibonacci number using multiple recursion.

public static long fib(int N) {
    if (N == 0 || N == 1) {
        return N;
    }
    return fib(N - 1) + fib(N - 2);
}

We can draw a recursion tree diagram to visualize the process for computing fib(N). Each node in the diagram represents a call to fib, starting from F(N), which calls F(N - 1) and F(N - 2). F(N - 1) then calls F(N - 2) and F(N - 3), and so forth. Repeated subproblems are highlighted in different colors.

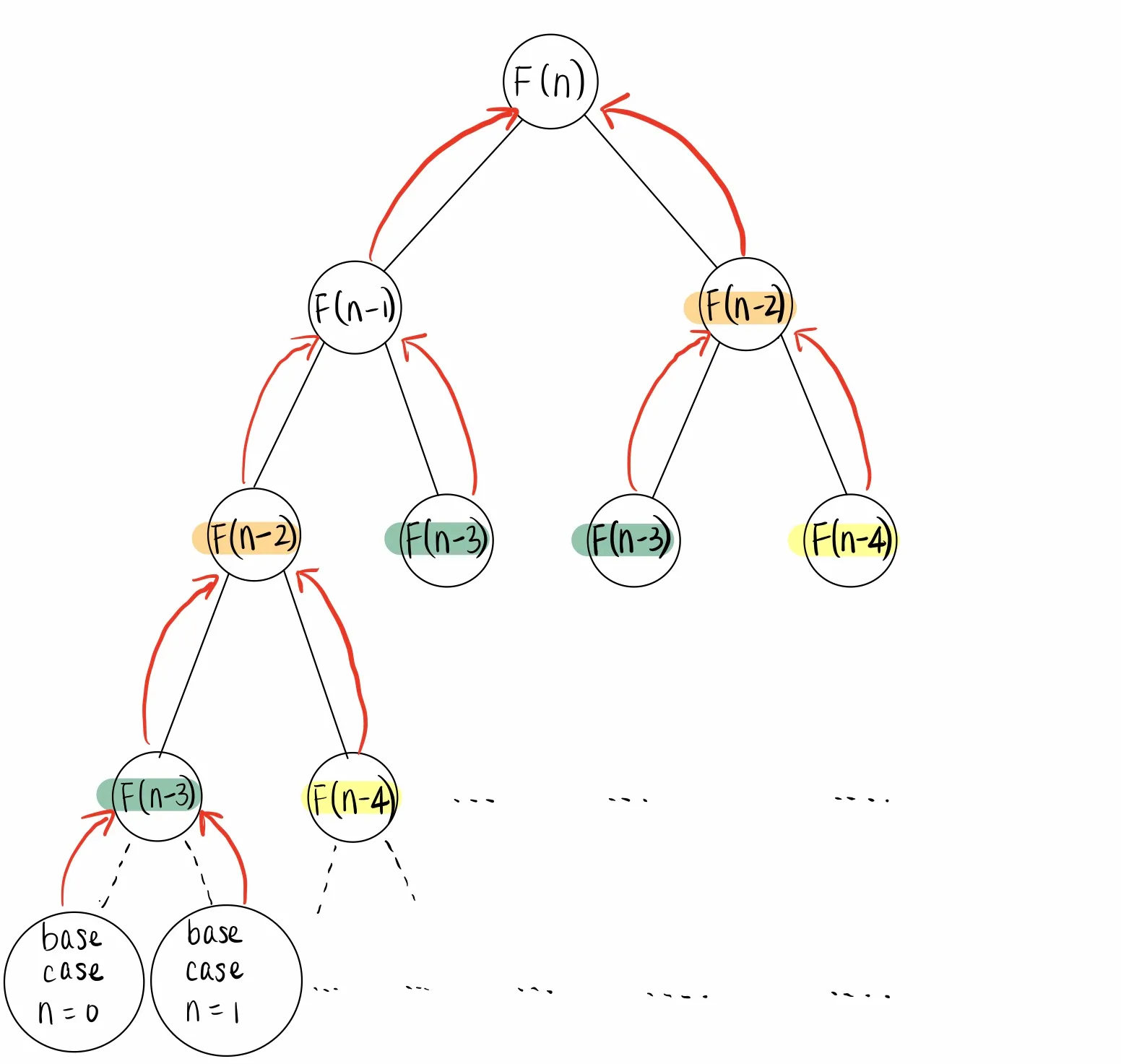
Fibonacci multiple recursion tree diagram

Top-down dynamic programming

To save time, we can reuse the solutions to repeated subproblems. Top-down dynamic programming is a kind of dynamic programming that augments the multiple recursion algorithm with a data structure to store or cache the result of each subproblem. Recursion is only used to solve each unique subproblem exactly once, leading to a linear time algorithm for computing the N^th Fibonacci number.

private static long[] F = new long[92];

public static long fib(int N) {
    if (N == 0 || N == 1) {
        return N;
    }
    if (F[N] == 0) {
        F[N] = fib(N - 1) + fib(N - 2);
    }
    return F[N];
}

Top-down dynamic programming is also known as memoization because it provides a way to turn multiple recursion with repeated subproblems into dynamic programming by remembering past results.

index	0	1	2	3	4	5	6
F(N)	0	1	1	2	3	5	8

The data structure needs to map each input to its respective result. In the case of fib, the input is an int and the result is a long. Because the integers can be directly used as indices into an array, we chose to use a long[] as the data structure for caching results. But, in other programs, we may instead want to use some other kind of data structure like a Map to keep track of each input and result.

Bottom-up dynamic programming

Like top-down dynamic programming, bottom-up dynamic programming is another kind of dynamic programming that also uses the same data structure to store results. But bottom-up dynamic programming populates the data structure using iteration rather than recursion, requiring the algorithm designer to carefully order computations.

public static long fib(int N) {
    long[] F = new long[N + 1];
    F[0] = 0;
    F[1] = 1;
    for (int i = 2; i <= N; i += 1) {
        F[i] = F[i - 1] + F[i - 2];
    }
    return F[N];
}

After learning both top-down and bottom-up dynamic programming, we can see that there’s a common property between the two approaches.

Dynamic programmming: An algorithm design paradigm for speeding-up algorithms that makes multiple recursive calls by identifying and reusing solutions to repeated recursive subproblems.

Eric Allender. 2009. A Status Report on the P versus NP Question. ↩