It’s A Graph Problem!¶
A seam is a path of adjacent or diagonally-adjacent pixels from one side of the image to the other, with exactly 1 pixel from each column/row, for horizontal/vertical seams respectively (opposite sides of an image are not adjacent, so seams cannot wrap around the image).
This subproblem looks much like a regular shortest path problem, since you would still be looking for a “path” of pixels to draw a line through. However, there are three important items to take into account:
- Each edge weight is based on a vertex (pixel) rather than the edge itself. So, you’ll have to calculate a weight based on pixels, but also decide where to put the weight on the edges.
- The goal is to find the shortest path from any of the pixels in the left column to any of the pixels in the right column or any of the pixels in the top row to any of the pixels in the bottom row.
- The graph has a regular structure assuming that the coordinates are in the prescribed ranges (which means that the graph is a directed acyclic graph (DAG)):
- There is a rightward edge to pixels , ,
and . - There is a downward edge from pixel to pixels , , and .
- There is a rightward edge to pixels , ,
Horizontal Seams¶
The findHorizontalSeam() method returns an array of length , where every entry stores the vertical position of the pixel to be removed from column of the image. For a less mathematical walkthrough of the return value, consider the 6-by-5 image (provided as 6x5.png) with the energy values shown in the table below.
| x=0 | x=1 | x=2 | x=3 | x=4 | x=5 | |
|---|---|---|---|---|---|---|
| y=0 | 980.51 | 616.11 | 525.98 | 510.59 | 293.90 | 428.73 |
| y=1 | 693.18 | 237.35 | 151.02 | 234.09 | 107.89 | 270.59 |
| y=2 | 279.81 | 138.69 | 228.10 | 133.07 | 211.51 | 295.34 |
| y=3 | 480.62 | 153.88 | 174.01 | 284.01 | 194.50 | 261.52 |
| y=4 | 686.84 | 456.94 | 450.47 | 544.76 | 575.77 | 933.10 |
Note
If you have previous background in matrix algebra or image processing, the array convention that you will see in this project may be different from what you are used to. Here, arr[x][y] refers to the pixel at x positions right of the leftmost edge of the picture, and y positions below the top edge.
The minimum energy horizontal seam is highlighted below. In this case, the method findHorizontalSeams() returns the array [2, 2, 1, 2, 1, 1] because the pixels in the minimum energy horizontal seam are (or, for every ):
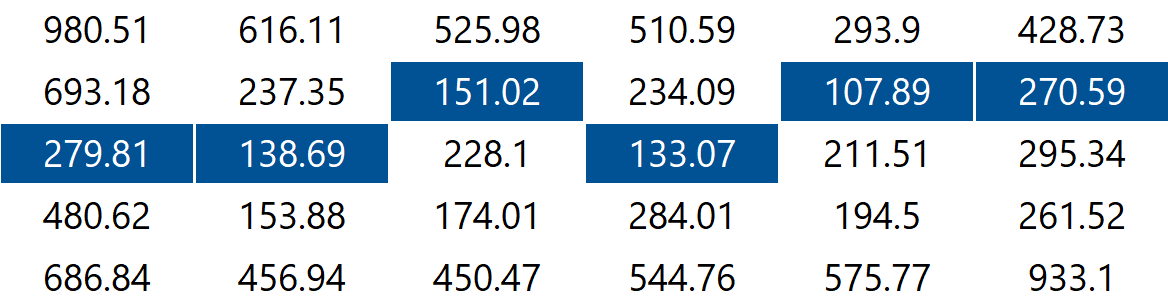
When there are multiple horizontal seams with minimal total energy, your method can return any of those seams.
Vertical Seams¶
The behavior of findVerticalSeam() is analogous to that of findHorizontalSeam() except that it should return an array of length such that every entry is the horizontal position of the pixel to be removed from row of the image.
For the 6-by-5 image, the method findVerticalSeam() returns the array [4, 4, 3, 2, 2] because the pixels in the minimum energy vertical seam are (or, for every ):
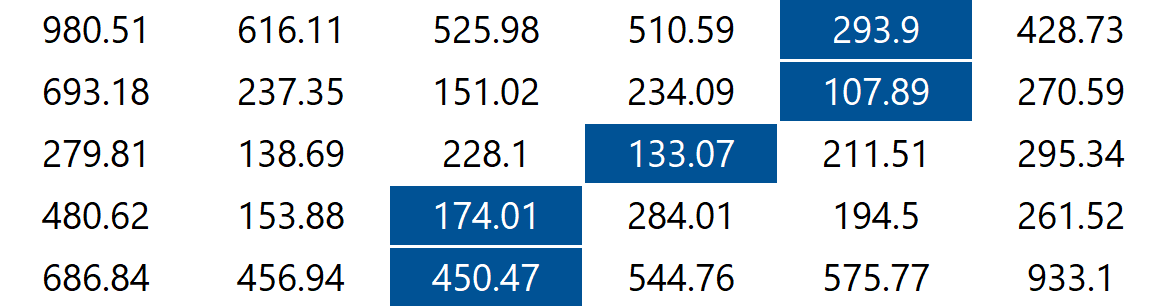
DijkstraSeamFinder¶
Task
Implement DijkstraSeamFinder
In order to get DijkstraShortestPathFinder to be able to remove seams, we’ll need to reduce the seam finding problem into one that’s solvable with a shortest path finder:
- Create the
Graphimplementation thatDijkstraShortestPathFinderwill operate on. - Set the actual reduction:
- Transform the
DijkstraSeamFinder’s input into one that works withDijkstraShortestPathFinder— instantiating the graph implementation and choosing our start and end vertices. - Convert the output of
DijkstraShortestPathFinderinto the format required forDijkstraSeamFinder.
- Transform the
Graph Implementation¶
Roughly, this is how you should represent your graph to be able to find seams:
- Vertices represent pixels.
- Edges exist from a pixel to its 3 adjacent, rightward or downward neighbors, for finding horizontal and vertical seams respectively.
- Edge weights represent the energy of each pixel.
- The shortest path (least total weight) represents the minimum energy seam.
Tip
You might have trouble cleanly representing this as a shortest path problem initially, because instead of a single starting point, the seam could start along any of the pixels in the leftmost or topmost column. In this case, it might be helpful to create dummy vertices and edges for the reduction.
Tip
How should you handle the edge cases of the border pixels? Think carefully about how you want to work with them, combined with the tip above.
Here is an example of how you may define your own Vertex class.
private static class YourVertex {
// Note: use "static" in the class header if it doesn't use any non-static fields
// in the outer class. Otherwise, remove the static keyword.
// ...
// implements equals
@Override
public boolean equals(Object other) {
// ...
}
// implements hashCode
@Override
public int hashCode() {
// ...
}
}
Here are some additional implementation notes that you should keep in mind as well:
- Don’t name the graph class
Graphsince that will conflict with thegraphs.Graphinterface. - The graph (and any other custom classes) must be declared as nested classes within the
DijkstraSeamFinderclass. If you write code in new files, our autograder will not be able to find them during grading. - The provided
pathFinderfield inDijkstraSeamFindersuggests what the graph and edge types should be, but you will also need to choose your own vertex object (either by selecting a suitable existing type or writing your own). Once you choose a vertex type (and being sure to update thepathFindertype definition to match the chosen vertex type), you can declare yourGraphsubtype to look something likeprivate class YourGraph implements Graph<YourVertex, Edge<YourVertex>> { // Note: use "static" in the class header if it doesn't use any non-static fields // in the outer class. Otherwise, remove the static keyword. // ... } - Since horizontal and vertical seams will need slightly different graphs, you may need to create two versions of the graph class or include logic to switch between horizontal and vertical versions (note that the vertical seam of a -by- image is just the horizontal seam of an -by- image).
Tests¶
Unlike previous projects, we have not provided many unit tests to test your implementation. Instead, we’ve included multiple images of various sizes in the seamcarving/data folder along with the expected energies and seams in .txt files. You should test your implementation by running the provided demo applications, and modify them as needed to test your implementation (or just for fun!):
-
The
SeamCarverVisualizercan remove either the horizontal or vertical seam:
-
The
PrintSeamsclass prints the numerical seams values to console. It might be helpful to manually check your results against the expected ones provided as text files in that folder.
Or, you can practice making your own tests using the provided text files.
Submission¶
Task
Submit to Gradescope and see if you pass all of the tests (info on grader-only tests). Once you are ready, add all of your project partners as Gradescope group members.
Warning
We consider misuses of Gradescope’s group feature to be academic misconduct. This includes submitting another student’s repository without tagging them as a group member, and similarly, adding another person who isn’t actually part of your project team as a Gradescope group member.
If you’re working in a group, the partner who submits must add the other partner as a group member on Gradescope. Here’s a video demonstrating that process. You’ll also need to re-add group members whenever you resubmit to the same assignment, even if you already did so on a previous submission.