Disjoint Sets Reading
Complete the Reading Quiz by noon before lecture.
The disjoint sets abstract data type supports two key operations: connect and isConnected. In Kruskal’s algorithm, our key concern is representing connected components. The runtime for this ADT will determine the runtime for Kruskal’s algorithm.
public interface DisjointSets {
/** Connects two items P, Q. */
void connect(int p, int q);
/** True if P, Q are connected. */
boolean isConnected(int p, int q);
}
In the example above, each integer in the disjoint set can be seen as a vertex in the graph. In Kruskal’s algorithm, we consider each edge in order of increasing edge weight. Before we can add an edge (p, q) to the MST, we need to first check that the two vertices (p and q) are not already connected. Then, we need to connect the two vertices. As a result, both connect and isConnect are important in our runtime analysis, so we need to make sure they’re fast. Let’s set our goal to be a logarithmic-time algorithm.
List of Sets
One slow but correct implementation is to use a List<Set<Integer>>. This is the most literal implementation of disjoint sets: each set in the list directly and literally represents the set in the ADT.
For instance, if we have N = 6 elements and nothing has been connected yet, our list of sets looks like {0}, {1}, {2}, {3}, {4}, {5}, {6}. After a few connect operations, it might look like {0, 1, 2, 4}, {3, 5}, {6}.
What is the runtime for isConnected in terms of N, the total number of elements?
O(N). We need to check that both p and q are in the same set. But we don’t necessarily know which set p is in nor which set q is in, so we may need to check all of the sets. If only a few sets have been connected, and p and q are in sets at the end of the list, then it’ll take order of N time to iterate overall the ~N sets.
What is the runtime for connect in terms of N, the total number of elements?
O(N) for the same reason as isConnected. In order to connect the items in two sets, we first need to know what’s in each set. But the only way to know what’s in each set is to find the set containing p and the set containing q in the list.
Data structures are only fast when we expect to know exactly or approximately where an item will be in the data structure. The List<Set<Integer>> representation is slow because we don’t know where each p and q will be in the data structure.
Quick Find
Quick find is the first of several faster implementations for Disjoint Sets. Suppose we know our number of items N up front. Create an int[N] where the indices of the array represent the elements of our set, and the value at an index is the set number it belongs to. This is similar to our array representation of a binary heap. The following image represents the disjoint sets {0, 1, 2, 4}, {3, 5}, {6}.
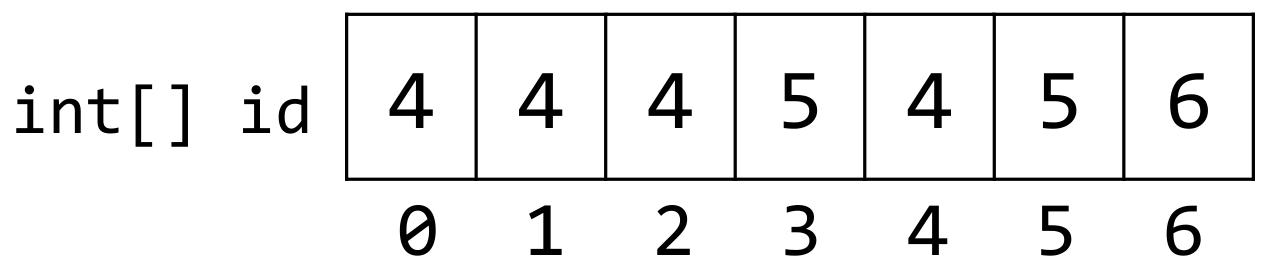
To connect(2, 3), first get id[2] and id[3] in constant time. Let’s say (arbitrarily) that id[3] (5) should be the new representative of the set. Iterate through the id array, setting all instances of 4 to 5. This last iteration step is an order of N runtime operation. But a slow connect enables a faster isConnected. isConnected(x, y) just needs to return id[x] == id[y] in constant time! As a result, we call this data structure quick find as the “find” operation is fast while the connect operation is slow.
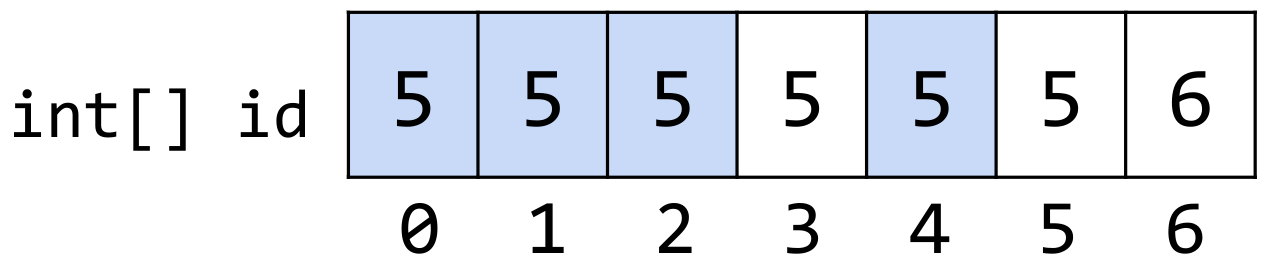
In lecture, we’ll see a family of other data structures based on the fundamental idea of quick find.