Minimum Spanning Trees Reading
Complete the Reading Quiz by noon before lecture.
In the past few lectures, we’ve solved a number of different graph problems: s-t connectivity (DFS), shortest paths on unweighted graphs (BFS), single-source shortest paths (Dijkstra’s), and single-pair shortest paths (A* search). Today, we’ll explore a different kind of graph problem: finding a minimum spanning tree.
Given an undirected graph, a spanning tree T is a subgraph of G, where T (1) is connected, (2) is acyclic, and (3) includes all of the vertices in G. Properties (1) and (2) make it a tree. Property (3) makes it a spanning tree.
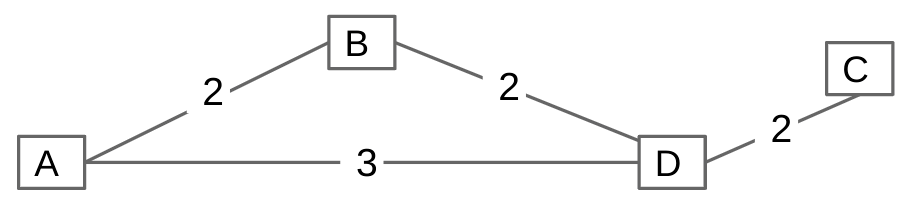
A minimum spanning tree is a spanning tree of minimum total weight. We might want to find the minimum spanning tree in order to determine the lowest cost to directly connect buildings with power lines.
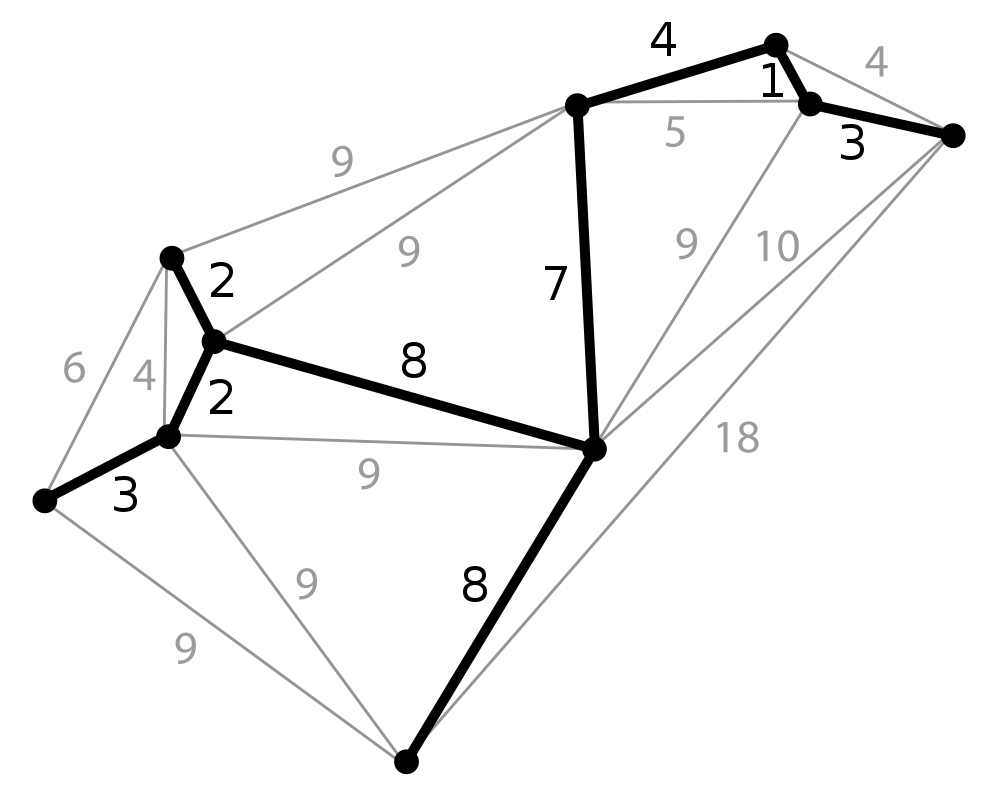
Find the MST in the undirected, edge weighted graph above.
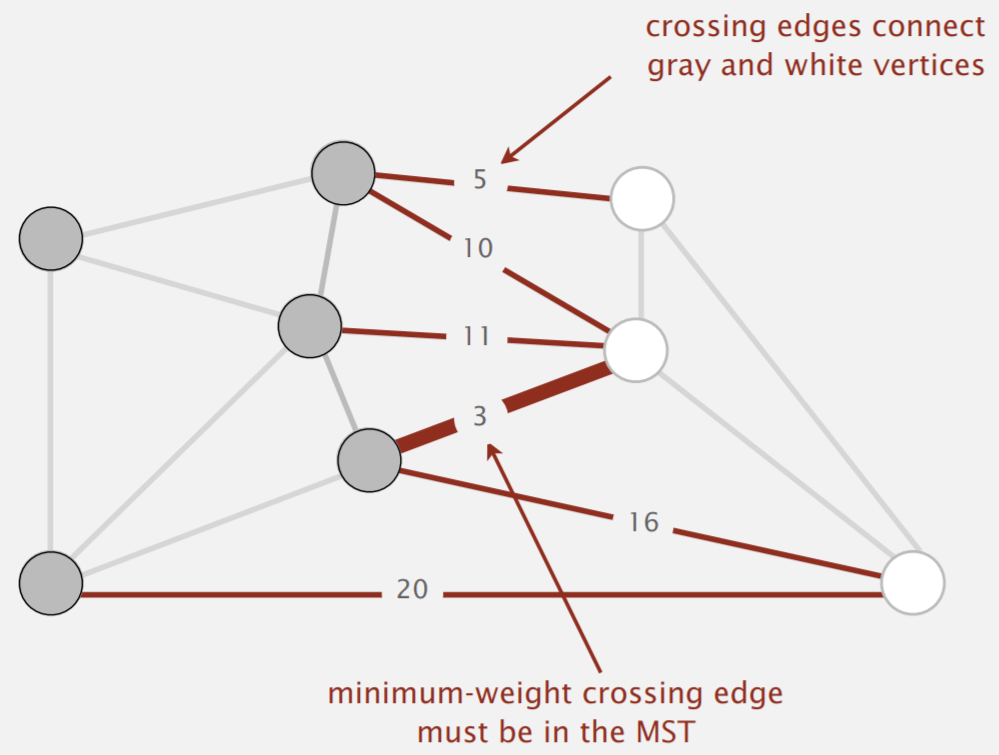
A useful tool for finding the minimum spanning tree is the cut property. A cut is an assignment of a graph’s nodes to two, non-empty sets. A crossing edge is an edge that crosses the cut, connecting nodes from one set to the other. The cut property states that, given any cut, a minimum-weight crossing edge must be in the minimum spanning tree.1
One way to see the cut property in action is to imagine a small example. Suppose we’ve almost found our minimum spanning tree, except for the vertex labeled 6 in the graph below.
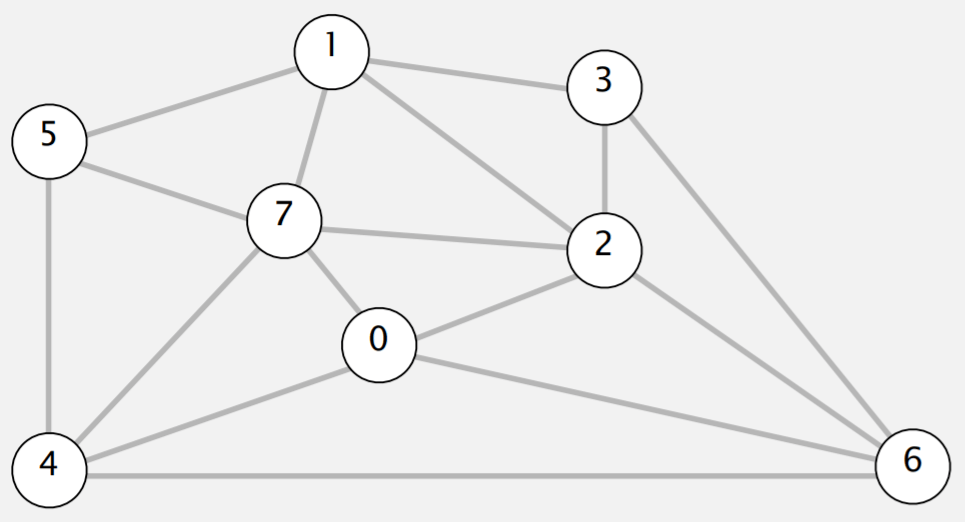
The only way to get to the vertex labeled 6 is using one of the four edges: (3, 6), (2, 6), (0, 6), or (4, 6). A minimum spanning tree must choose a minimum-weight edge among the four options.
We can also design an algorithm for finding the minimum spanning tree based on this insight by working backwards from this idea. Suppose we start from scratch in the same graph above. If we (arbitrarily) choose to start at the vertex labeled 6, then the cut property tells us that we must choose a minimum-weight edge among the four options. This is the basis of Prim’s algorithm for finding a minimum spanning tree.
Robert Sedgewick and Kevin Wayne. 2019. Minimum Spanning Trees. In COS 226: Algorithms and Data Structures, Fall 2019. https://www.cs.princeton.edu/courses/archive/fall19/cos226/lectures/43MinimumSpanningTrees.pdf ↩