Shortest Paths Reading
Complete the Reading Quiz by noon before lecture.
In the previous lecture, we learned about how different graph implementations resulted in different runtimes for depth-first search and breadth-first search.
- DFS
- Find a path from a given vertex, s, to every reachable vertex in the graph.
- BFS
- Find a shortest path from a given vertex, s, to every reachable vertex in the unweighted graph.
When we introduced breadth-first search, we also determined that it wouldn’t be good for a navigation tool like Google Maps. BFS is an algorithm that returns the shortest path in terms of number of edges, not the total distance. However, in the real world, the distance between roadway intersections is not always the same.
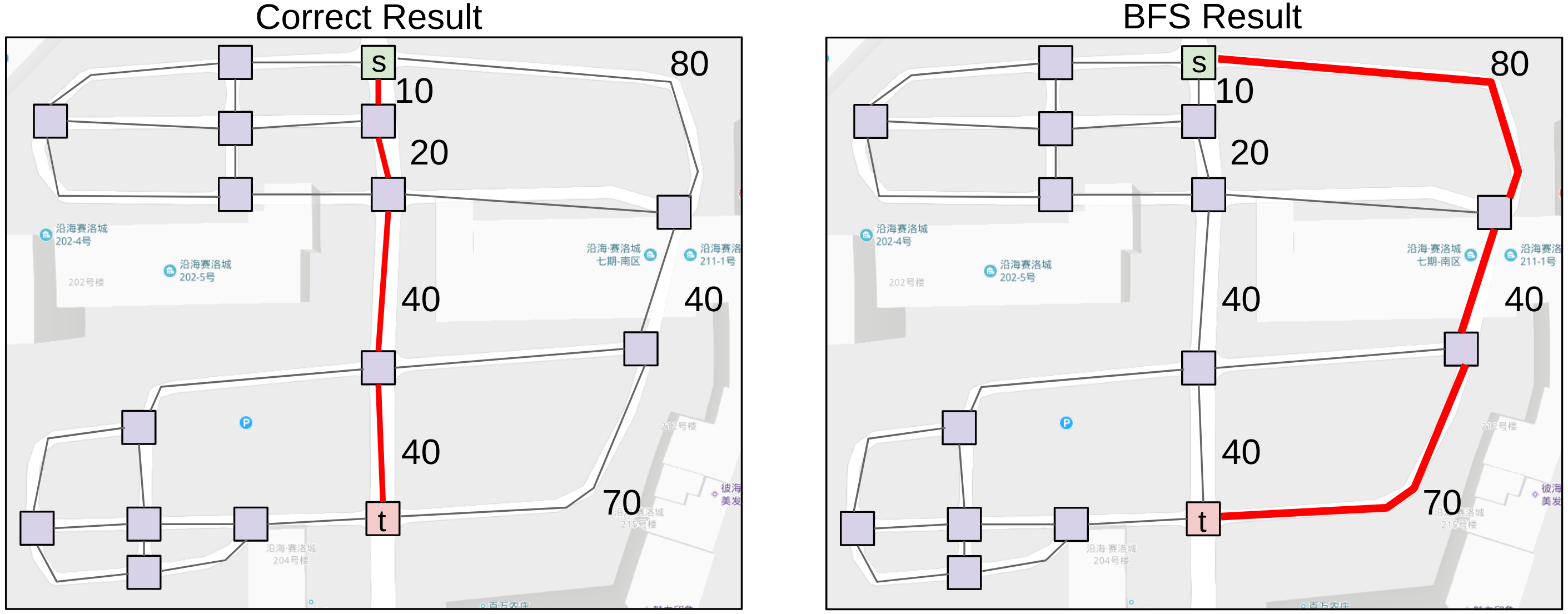
Now, let’s work through an example by hand, taking into account edge weights. Suppose we have the following weighted, directed graph.
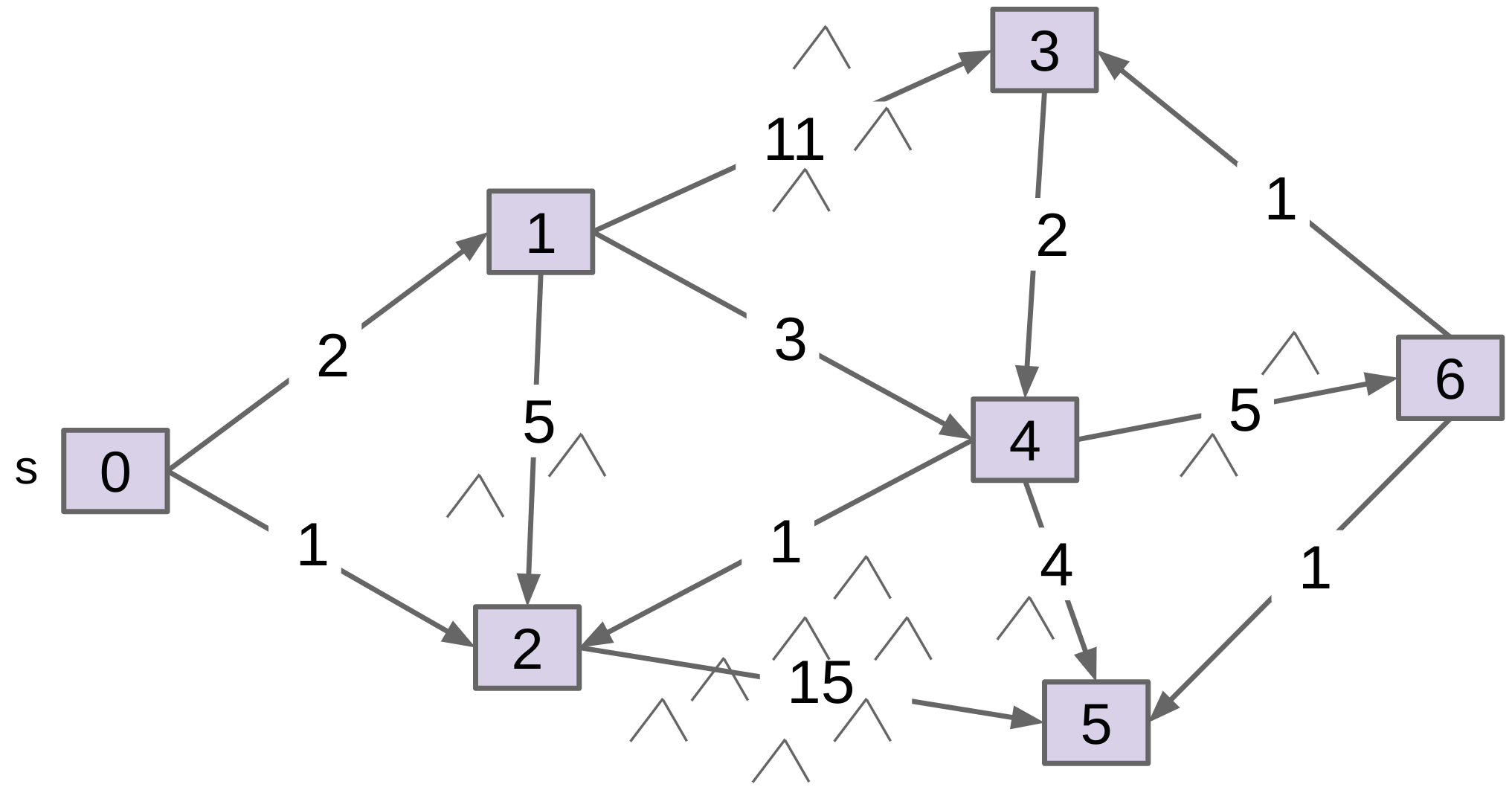
Find a shortest path from the vertex 0 to the vertex 5.
Notice that the shortest path can contain many edges. Our goal is to find the path from 0 to 5 that minimizes the total sum of the edge weights.
Find the shortest path from 0 to every other vertex.
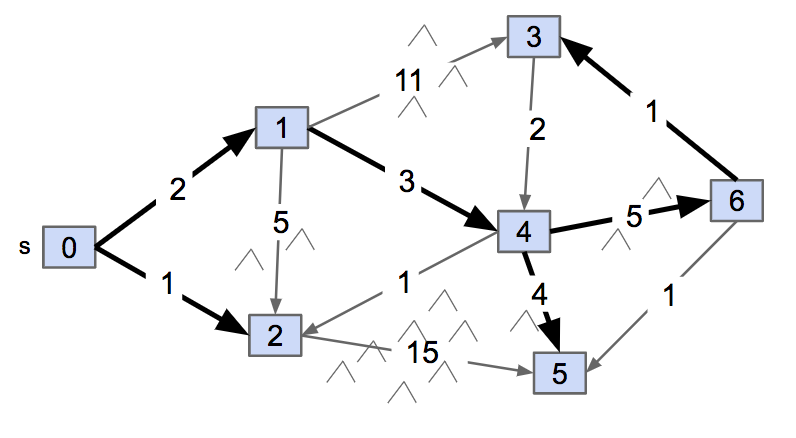
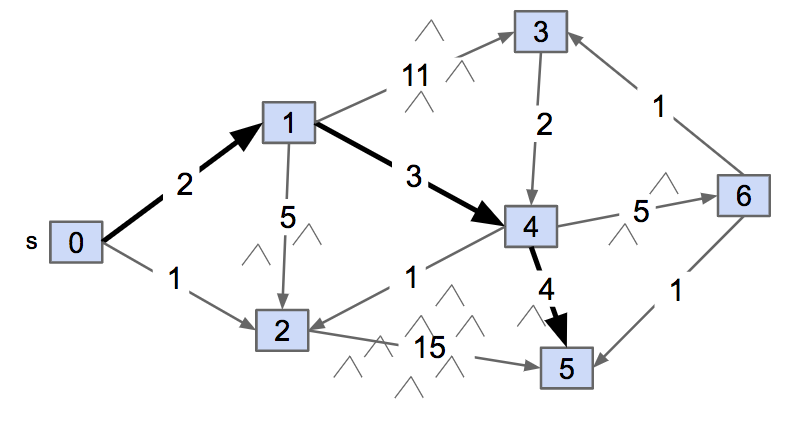
Similar to BFS, computing the shortest path from 0 to every other vertex results in a tree! Because we used an edgeTo array in BFS, each vertex contains one parent—which results in a tree structure with s as the root.
The shortest path from 0 to 5 that we found earlier uses the shortest path from 0 to 4 and then the edge from 4 to 5. And we can see this pattern across the entire graph. The shortest path from 0 to 4 uses the shortest path from 0 to 1 and the edge from 1 to 4. The shortest path from 0 to 1 uses the shortest path from 0 to 0 (a distance of 0!) and the edge from 0 to 1.
The shortest paths tree results from searching the graph by exploring the frontier. Finding the shortest path from 0 to 1 helps us find the shortest path from 0 to 4, which helps us find the shortest path from 0 to 5, from 0 to 6, and from 0 to 3. Using this idea, we can develop a shortest path algorithm based on breadth-first search swapping out the queue for a priority queue ordered on distance from the source vertex.
This algorithm, called Dijkstra’s algorithm, solves the single-source shortest paths problem: given a single source vertex s in a (weighted) graph, find the shortest paths from s to all other vertices. See the DijkstraSP.java class for more details.
public class DijkstraSP(EdgeWeightedDigraph G, int s) {
// G cannot have negative weights
distTo = new double[G.V()];
edgeTo = new DirectedEdge[G.V()];
pq = new ArrayHeapMinPQ<Integer>(G.V());
pq.insert(s, 0.0);
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
// relax vertices in order of distance from s
while (!pq.isEmpty()) {
int v = pq.removeSmallest();
for (DirectedEdge e : G.adj(v))
relax(e);
}
}
// relax edge e and update pq if changed
private void relax(DirectedEdge e) {
int v = e.from(), w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
if (pq.contains(w)) pq.changePriority(w, distTo[w]);
else pq.add(w, distTo[w]);
}
}