Red-Black Trees
Complete the Reading Quiz by noon before lecture.
B-Trees are complicated to implement for a number of reasons. For one, maintaining different node types adds complexity when converting back and forth between 2-nodes and 3-nodes. There are also a large number of cases for handling node splitting behavior correctly. Let’s setup the groundwork for identifying a better way to develop a balanced search tree based on what we learned about B-Trees.
We saw in the previous lecture that, depending on the order items are inserted into the tree, there are many different ways to construct a binary search tree containing the same set of items. For example, there are five possible binary search trees for the set of numbers 1, 2, and 3.
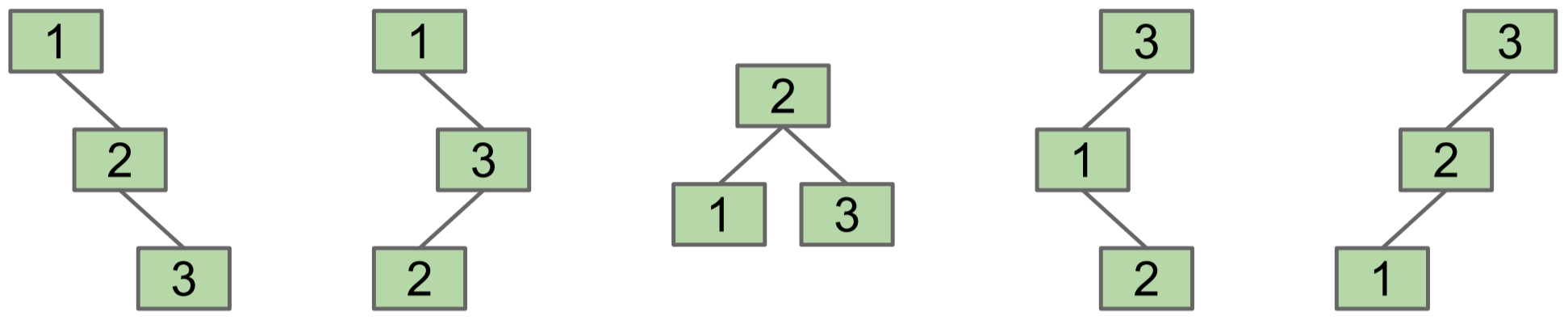
Give an insertion order for the tree of minimum height containing the set of numbers 1, 2, and 3 as shown in the middle of the above image.
Either 2 1 3 or 2 3 1 would work.
However, insertion is not the only way to yield different configurations of the same set of items. One thing we can do is change the structure of the tree through a process called rotation.
Rotation
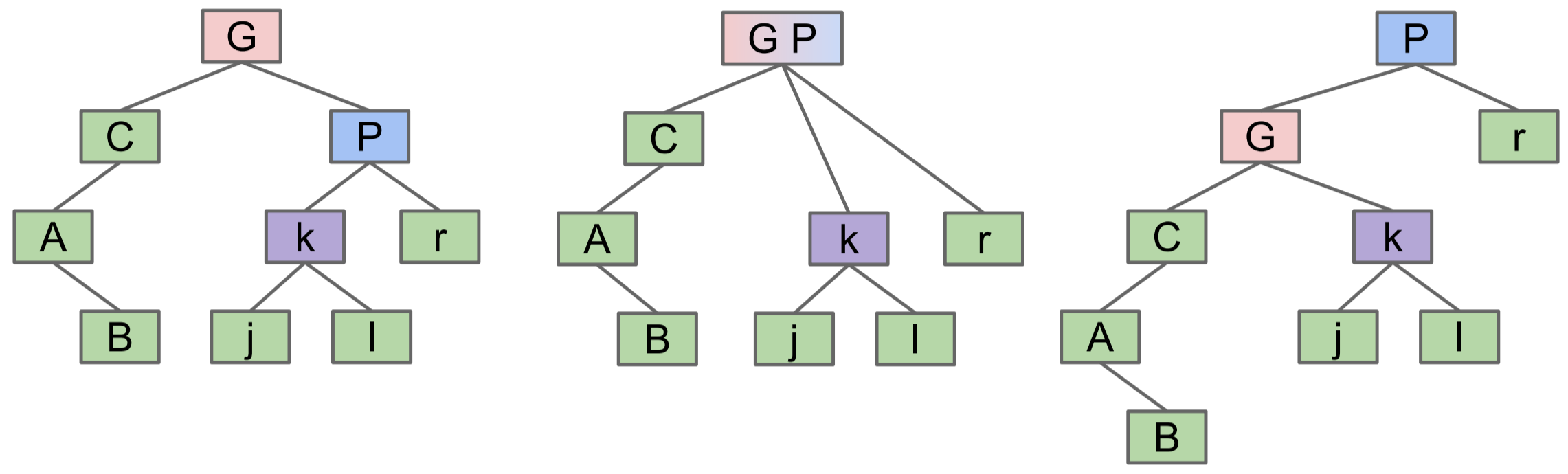
Given a particular node in a tree, we can either rotate it to the left or to the right by making it the child of one of its parents. In these definitions, G and P correspond to their labels in the tree shown below.
rotateLeft(G)
Let x be the right child of G. Make G the new left child of x. We can think of this as temporarily merging G and P, then sending G down and left. In the example below, the height of the tree increases as a result of rotating left around G.
rotateRight(P)
Let x be the left child of P. Make P the new right child of x. We can think of this as temporarily merging G and P, then sending P down and right. In the example below, the height of the tree decreases as a result of rotating right around P.
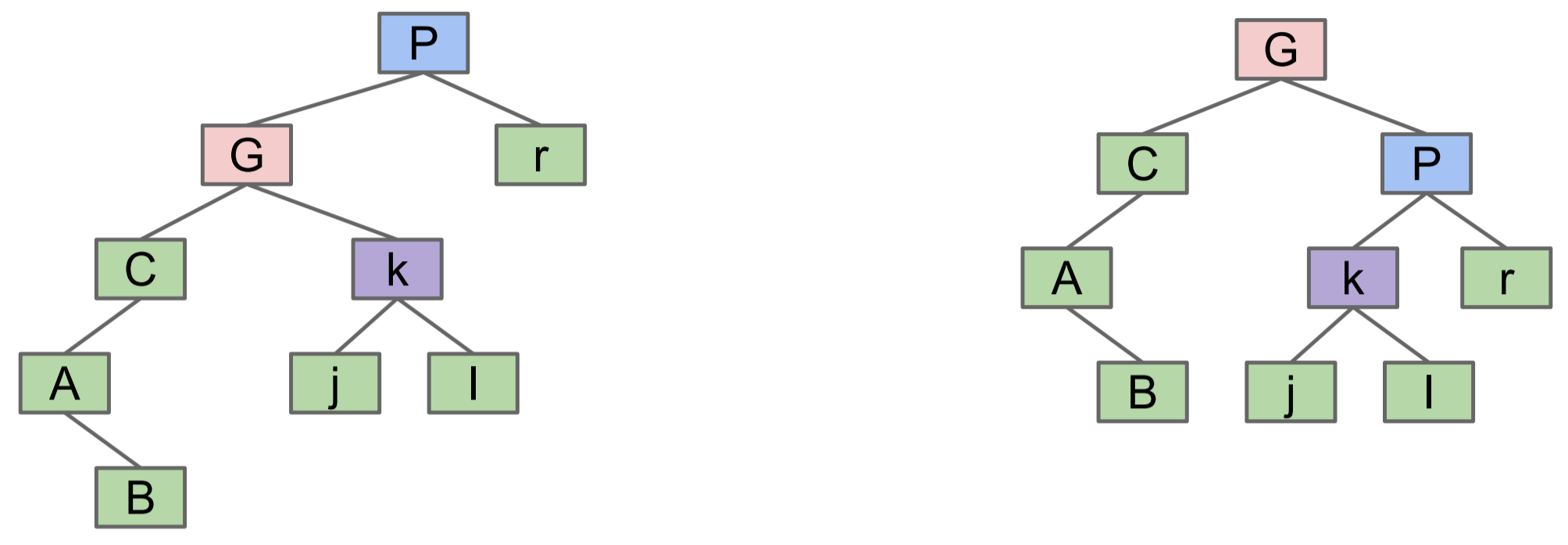
Let’s see how this plays out on a small example.

Give a sequence of rotation operations that balances the tree on the left.
One possible solution is to rotateRight(3) first and then rotateLeft(1). There are other correct answers too.
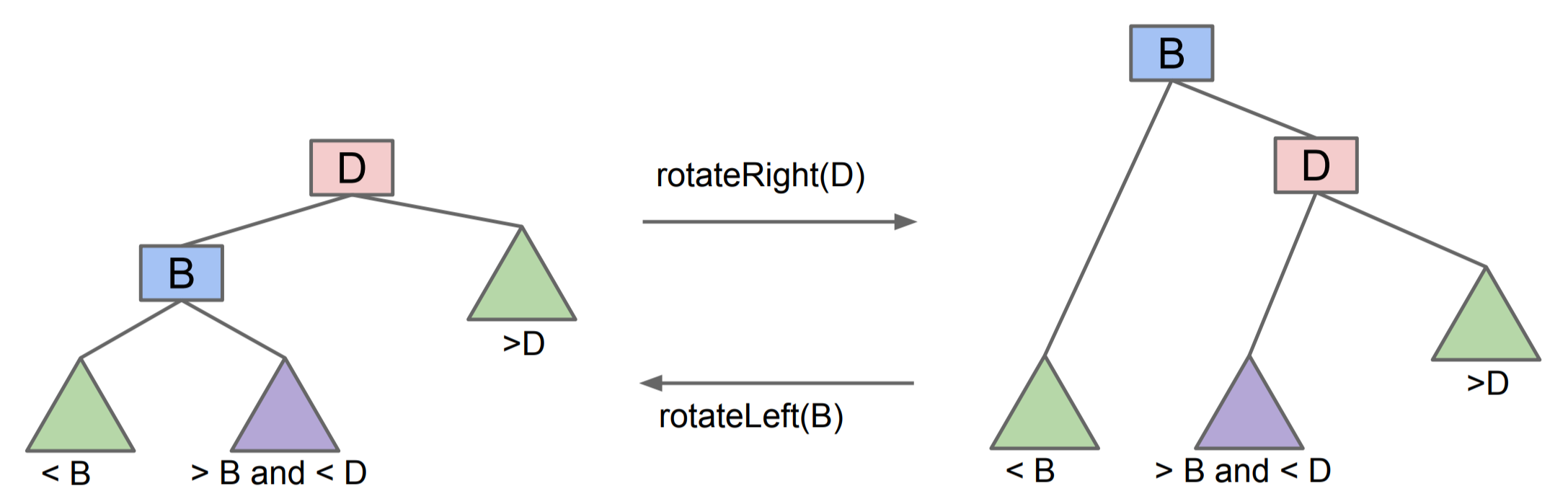
More generally, rotations work because they respect the binary search tree ordering invariant. Items that are ordered between B and D in the example below stay ordered between them after a rotation.
Josh Hug has prepared a slideshow showing how to balance a tree through a sequence of rotations. Each rotation makes a small, local adjustment that gradually balances the tree, sometimes increasing or decreasing the height of the tree. It’s too slow to rebalance the entire tree this way from scratch, so in lecture we’ll see how we can use rotation to maintain the balance of the tree in the same way that B-Trees maintained balance by occaisionally splitting nodes.