Algorithm Analysis II
Complete the Reading Quiz by noon before lecture.
Table of contents
In the previous lecture, we learned the fundamental principles and a process for analyzing the runtime of a program. In this reading, we will apply the runtime analysis procedure to a sorting algorithm called selection sort. The goal of a sorting algorithm is to rearrange an array of N items into ascending (sorted) order. When studying sorting algorithms, we count comparisons and swaps between pairs of items in the array.1 This will be our cost model.
Selection sort
- Selection Sort
- Repeatedly select the smallest remaining item and swap it to its proper index.
- Find the smallest item in the array, and swap it with the first item.
- Find the next smallest item in the array, and swap it with the next item.
- Continue until all items in the array are sorted.
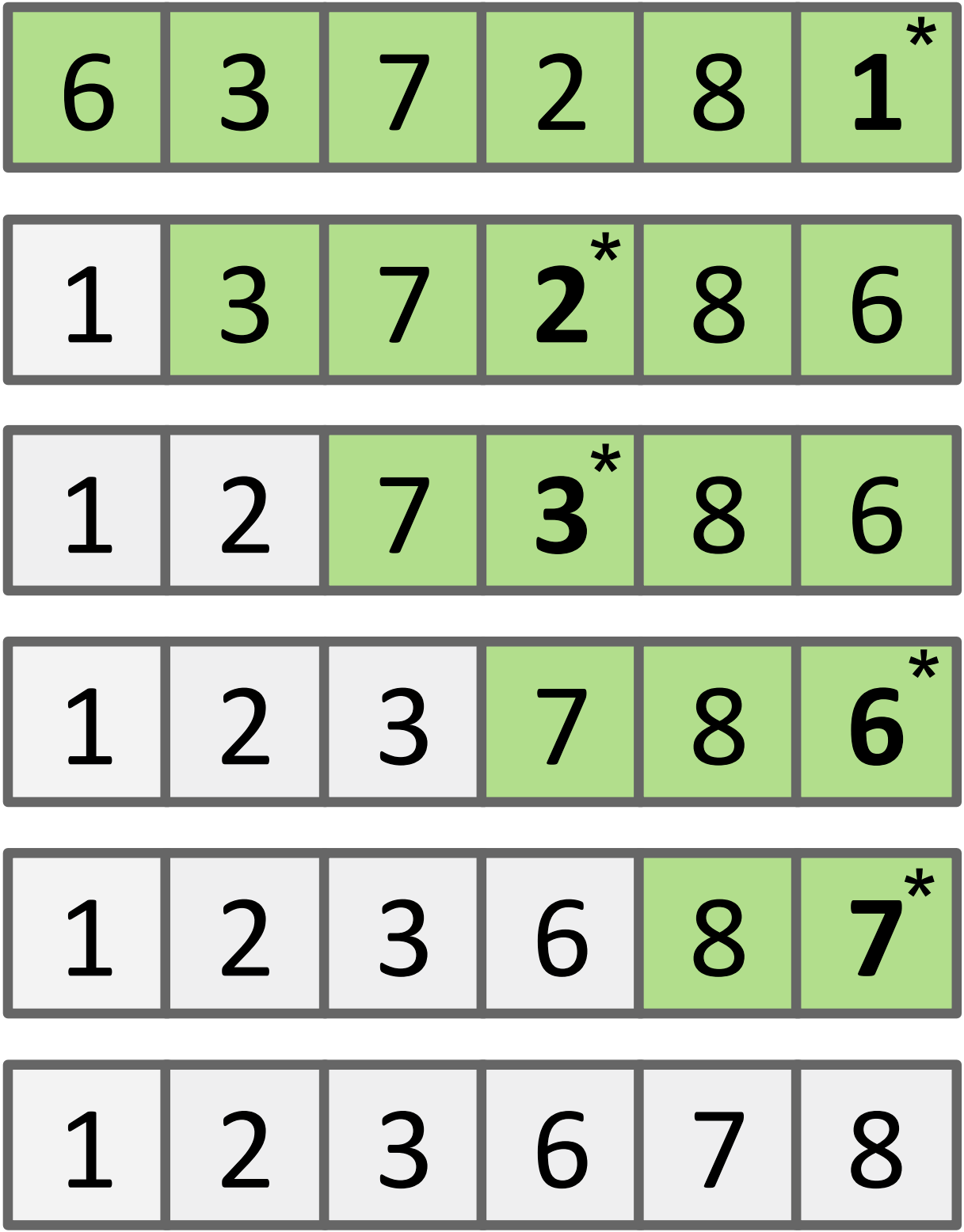
In this example, the array begins unsorted with the items 6 3 7 2 8 1. To find the smallest item in the array, selection sort scans across the entire array and swaps the value 1 with the first item in the array. To find the next smallest item in the array, selection sort scans across all but the first item in the array (since we know it’s the smallest) and swaps the value 2 with the next item in the array.
Simplified modeling process
How would we analyze the order of growth for the runtime of selection sort with respect to N, the size of the input array, using the simplified modeling process?
- Choose a representative operation to count (cost model).
- Figure out the order of growth for the count of the representative operation by either:
- Making an exact count and then discarding the unnecessary pieces.
- After lots of practice, using inspection to determine order of growth.
We can use the number of comparisons and swaps as our cost model, so we need to figure out the order of growth for comparisons and for swaps. Let’s consider comparisons first.
How many comparisons does it take to find the smallest item in the array in terms of N, the number of items in the array? How about finding the next smallest item?
It takes N - 1 comparisons to find the smallest item. We can keep track of the smallest item we’ve seen so far in the array and iterate across, comparing each item against the smallest seen so far, updating it as necessary. Initially, the smallest item seen so far is the first item, so we don’t need to compare it against itself.
By the same logic, it takes N - 2 comparisons to find the next smallest item.
The pattern continues until all N items are sorted.
What is the order of growth for number of comparisons in selection sort with respect to N, the number of items in the array? Explain your answer in two ways: using an exact count as well as a geometric argument.
The exact count is N(N - 1) / 2, following the same logic as our analysis for dup1. The green-shaded cells from the example forms a right triangle representing roughly the number of comparisons needed. We know the area of a right triangle with side length N - 1 is roughly N2 / 2.
Try following the same steps and analyze the number of swaps on your own.
What is the overall order of growth of the runtime for selection sort? Give your answer using asymptotic notation.
The number of comparisons has an order of growth of N2 while the number of swaps has an order of growth of just N.
Therefore, the overall order of growth of the runtime for selection sort is in Theta(N2).
Case analysis
Selection sort does not have different cases.
Why doesn't the selection sort algorithm have a best or worst case runtime analysis?
There are no shortcuts to finding the minimum item. We always have to check all of the unsorted items in the array to be sure that we’ve found the smallest item. This is true no matter the contents of the array.
Some sorting algorithms don’t swap items, in which case we can count the number of array accesses. ↩