
Assignment A5: Applying UNION-FIND
Overview
In this assignment, we will be applying the UNION-FIND technique. We'll use it for two different image-processing operations. One is determining and labeling the connected components of a spatial data structure. The other is segmenting the pixels of an image into regions ("segmentation"). The latter is in the optional extra-credit portion of Part II.
Part I (Due Wednesday, February 17, at 11:59 PM -- 30 points)
I.1. UNION-FIND and Corporate Mergers
Suppose the following companies begin as small startups:
Acme, Biocybo, CryoBio, DigiToe, Exxoff, Fibon, GIGO, Hashco, iWin, and Junkium.
The following sequence of corporate mergers take place, and in each case, the new entity
adopts the name of that company (which is taking part in the merger) whose name was closer to the beginning of the alphabetical
list. For example, if iWin and Junkium merge, the new company's name is iWin.
The merge operations are called UNION.
Identifying the new company which owns and old company is done by the FIND operation.
Q1a. Suppose that the following operations are performed in sequence. Give the results of each FIND operation. No answer is required for UNION operations. Include in your answer the results for the FIND operation at step 2, even though it is given to you as an example.
1. UNION Biocybo, CryoBio 2. FIND Biocybo (answer: Biocybo) 3. FIND CryoBio 4. UNION Junkium, Digitoe 5. UNION Acme, Digitoe 6. FIND Exxoff 7. FIND Junkium 8. UNION Fibon, Hashco 9. UNION iWin, Biocybo 10. FIND Hashco 11. FIND iWin 12. UNION Fibon, Biocybo 13. FIND Hashco 14. UNION Biocybo, Acme 15. FIND CryoBio
Q1b. Draw the 10 companies as nodes of a graph, with approximately the following spatial layout. Put each company name inside its own circle. If you wish, you may print out the portion of this page containing these names, draw on the printout, take a legible photo of your drawing, and load that into your assignment answers document.
Acme Biocybo CryoBio, DigiToe Exxoff Fibon GIGO Hashco iWin Junkium.
Then draw the forest of up-trees that results from performing all the UNION operations in the sequence above. You don't need to redraw after each UNION; just show the final forest of uptrees. (Do not perform any path compression here.)
I.2. UNION-FIND and Point Set Merging
Consider the following set of vertices, analogous to that above. Here, instead of corporate
names, each vertex is identified by an (x,y) coordinate pair.
![]()
Q2a. Once again, show the results for the FIND operations, but use this new set of items and the following sequence. Assume that a UNION (x0,y0), (x1,y1) operation leads to a subset with name (x0,y0) if either (x0 < x1) or (x0 = x1 and y0 < y1), and to a subset with name (x1,y1) otherwise. Also, let us define a new operation FIND_UNION A, B to be equivalent to UNION FIND(A), FIND(B). (Don't show the results for the embedded FIND operations in FIND_UNION.)
1. FIND (2,1) 2. FIND_UNION (1,2), (2,2) 3. FIND_UNION (1,1), (2,1) 4. FIND_UNION (3,2), (3,3) 5. FIND_UNION (1,3), (2,3) 6. FIND (3,3) 7. FIND (2,3) 8. FIND_UNION (3,1), (3,0) 9. FIND_UNION (3,2), (3,1) 10. FIND (3,3) 11. FIND_UNION (0,3), (1,3) 12. FIND_UNION (0,1), (0,2) 13. FIND (1,3) 14. FIND_UNION (1,0), (2,0) 15. FIND_UNION (0,3), (0,2) 16. FIND (2,3) 17. FIND_UNION (0,0), (0,1) 18. FIND (1,3) 19. FIND (1,2) 20. FIND_UNION (2,2), (3,2) 21. FIND_UNION (2,0), (3,0) 22. FIND (3,3) 23. FIND (1,1)
Q2b. Now draw the forest of up-trees that results from performing all the UNION operations in the sequence above. (Again, do not perform any path compression here.)
I.3. Connected Components of an Image
We define the strict pixel graph of an image to be the pair Gs = (V, E), where V is the set of pixels, like those shown above in the diagram for the previous exercise. Then E is the set of edges, where an edge e connects v0 = (x0, y0) with v1 = (x1, y1) provided | x0 - x1 | + | y0 - y1 | = 1 and the colors of the two pixels are equal. The strict pixel graph is undirected.
Consider the simple digital image below, in which each pixel's color is represented by just a single
letter. Here we can imagine Y = yellow, M = magenta, G = green.
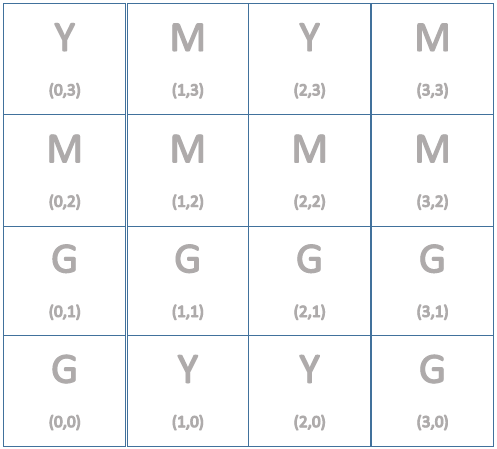
Q3a. Draw the strict pixel graph on top of a copy of the image. The edges should be undirected.
Q3b. How many connected components are there in this graph? (A connected component C of a graph G is a subgraph of G that is connected within itself, and not connected to any vertices of G outside of C.) The number of connected components of an image is often used as an estimate of the number of separate objects or graphical elements in the image.
Q3c. Number the connected components starting at 1. The components should be ordered according to the minimum pixelID value in them, where a pixelID for the pixel at (x,y) is y*w + x, where w is the width of the image in pixels (i.e., w is the number of columns in the image). The connected component containing the pixel at (0,0) should get number 1. Write a 1 on each pixel in that component. Find the next component by scanning the pixels in order of increasing pixelID values until you find a pixel that is not in a component already labeled. Label each pixel in this new component 2, etc., until you have labeled all the pixels of all the components. (By using pixelID values, we will be able to avoid the awkwardness of naming subsets using ordered pairs as we did in Q2a.)
Part II. Implementation of Connected Components (70 points)
Using the main starter code and ProgressiveColors.java helper file, implement the features described below. The test image to use is a scan of the first page of Abraham Lincoln's Gettysburg Address, not only an appropriate reminder about Veterans Day, but a good example of a bicolor image having many connected components, each corresponding to a word of the document (although there are also some connected components that represent individual characters of text, and there are a number of separate connected components that represent parts of the background -- the paper on which Lincoln did his handwriting).
II.1. Finding the Connected Components of an Image.
Using a two-dimensional int array of pixelID values, named parentID, write code that applies the UNION-FIND method, as in Exercise Q2b, to build a forest of up-trees for the current image. Each element of parentID will either be the pixelID value of the parent of the up-tree node, or -1 if the node itself is the root of an up-tree. Initially, before any of the UNION operations, each element of the array should be -1, since every pixel is in its own subset.
You should write a pair of methods getXcoord and getYcoord that will return the x and y coordinates of the pixel having a given pixelID value. Then it will be possible to follow the path from any pixel to the root of its up-tree by repeatedly getting the parent node's pixelID from the parentID array, and then from the pixelID getting the x and y coordinates of the parent, and then getting the its parent's pixelID, etc., until the root of the up-tree is reached. Implement the FIND method to perform that path following and return the pixelID of the root.
Your UNION method should take two pixelID values representing roots of up-trees, and it should make the one having the smaller pixelID value be the parent of the other.
Now apply your UNION-FIND implementation to the problem of analyzing an image. Your code will merge groups of pixels so that, at the end, each connected component of the strict pixel graph will be represented by one up-tree.
To do this, your code should scan the image considering all the pixel pairs for which edges exist (according to the definition of Gs, in Part I). Perform FIND_UNION on all such pairs. Starting at (x, y) = (0, 0), check to see if Gs contains an edge to (x+1, y) = (1, 0) and/or to (x, y+1) = (0, 1). If it does, perform the FIND operations on the endpoints of this edge, and if the results are different, then UNION the two subsets. After processing this pixel, go on to the next (incrementing x). When the first row of pixels is complete, do the same for the second row, etc., until all rows of pixels have been processed.
Instrument your UNION method, so that a count is maintained of the number of times UNION is called. That count should be set to zero before the scan begins. At the end, print out the count in the following style.
The number of times that the method UNION was called for this image is: 2764.
II.2. Counting the Connected Components
Next, set an integer variable, count, to zero, and do another scan of the parentID array. Each time a root of an uptree is encountered, increment count. At the end of the scan print out the value of count with explanatory text as follows:
The number of connected components in this image is: 79.
Note that the number of times UNION was called, plus the number of connected components found should add up to the number of pixels in the image, so you can use this fact in debugging your code.
II.3. Labeling the Connected Components
Now modify your code (that does the scanning and counting above) so that each time an uptree root is encountered, not only is the count incremented, but that root is associated with the count in a hashtable named componentNumber. Thus the keys of your hashtable will be of class Integer (representing the roots' pixelID values), and the values will also be of class Integer (representing the counts -- i.e., the connected component numbers).
Write code for another scan of the image, this time doing the following for each pixel: (a) FINDing the root of the pixel's up-tree; (b) Looking up the count value for that root in the hashtable. (Then convert the Integer to an int.) Let's call the resulting int k. (c) Determine the kth progressive color by calling the provided method getProgressiveColor(k). (d) Replace the rgb information of biWorking with the new color.
When the scan is complete, the method repaint() should be called to show the newly colored image.
Here is what your image should look like, after you have completed the labeling for the
given image of page 1 of Lincoln's Gettysburg Address. The colors may
depend on your scanning order and how you implement the UNION operation. However, we would
expect the image to look like this, assuming you are following the specifications given above.
(Thanks to CSE graduate student Johnson Goh for providing this example.)

Turn in your source files through our Catalyst CollectIt dropbox. Part II of this assignment is due Monday, February 22 at 11:59 PM. Late penalties apply (see the policies page for details).
Extra Credit: Image Segmentation with Kruskal's Minimum Spanning Tree Algorithm (10 points of extra credit)
After completing the required portion of Part II, you've got an implementation of the UNION-FIND abstract data type that we can re-use for a more general problem than the connected-components analysis. When the connected components were found, the pixels within a component had to have exactly the same color values. With our new method, we won't require exact matches, and we'll set our merging criteria to work on the basis of number of components rather than color equivalence or differences.
To make this activity even more interesting, we'll integrate the use of a priority queue. We will also use the graph-theoretic constructs of minimum spanning trees and minimum spanning forests.
II.4. The Weighted Pixel Graph.
In Part I, we defined the strict pixel graph for an image to have an edge between adjacent pairs of pixels, provided they had the same color. We now define the weighted pixel graph for an image to have an edge between every adjacent pair of pixels, regardless of color. However, each edge also carries a numeric weight. We define the weight to be the squared Euclidean distances between the colors of the corresponding pixels. (This is the same distance metric used in Assignment 4, Part IIB for comparing the colors of pixels in the image with colors in the palette.) For an example of an image and its weighted pixel graph, see the worksheet (planned for Wednesday, Feb. 17) and its solutions (to be given).
II.5. Minimum Spanning Forests.
Given a weighted undirected graph G=(V,E) with nonnegative weights, and an integer N, a minimum spanning forest of size N for G is a subgraph G'=(V, E') such that G' contains N connected components Ci, and no other subgraph G''=(V, E'') having N connected components has total weight lower than the total weight of E'.
Note: this is a "generalized" minimum spanning forest definition that allows G to be broken up into separate connected components. For a given value of N (number of regions), there may be a set of alternative minimum spanning forests that tie for lowest total weight, due to the presence of edges of equal weights.
Note also that if N = 1, then G' contains exactly one connected component, and G' is a minimum spanning tree for G.
The worksheet solution mentioned earlier shows a minimum spanning forest having 3 trees for the weighted pixel graph of an image.
II.6. Image Segmentation into Regions.
An image segmentation is a partition of the image's pixels into a set of regions {R0, R1, ..., Rm-1} such that each Ri is a four-connected set of pixels (there is a path within the region from any member u to any other member v, consisting of steps that go only north, south, east, or west), the pixels obey a color constraint, and the partition is maximal -- any additional merging would either violate the connectivity requirement or the pixel color constraint.
We'll now define a version of image segmentation based on finding a minimum spanning forest for the weighted pixel graph of an image. Each pixel of the image is represented by one vertex in the graph, and each region in the segmentation will be represented by one tree in a minimum spanning forest.
The color constraint is of the following type. Any two adjacent pixels, if they are in the same region Ri must have a squared color difference less than or equal to DELTA, where DELTA is a contrast limit set either by the user or by the segmentation algorithm on the basis of how many regions to find.
II.7. Kruskal's Algorithm.
To find the minimum spanning forest for a given number of regions or a given DELTA, we do the following. Initialize a UNION-FIND structure (e.g., using the parentID scheme from Part II) with each pixel in its own subset.
Initialize the set E of edges of the weighted pixel graph, and insert them all into a priority queue Q. Note that we have to compute the weights, since those serve as priority values in Q.
Optional, and only for debugging on small images: Maintain a set E' of minimum spanning forest edges, and initialize it to the empty set: E' = {}.
Begin a loop, during which the minimum spanning forest is constructed:
Finished = False
nTrees = numberOfPixelsInTheImage
While not finished,
e = Q.deleteMin()
w = weight(e)
if w > DELTA or nTrees <= nRegionsDesired:
finished = True
break;
u = endpoint1(e)
v = endpoint2(e)
rootu = find(u)
rootv = find(v)
if rootu != rootv:
union(rootu, rootv)
nTrees -= 1
(optional) insert e into E'
print "Done finding minimum spannng forest"
From here, the algorithm proceeds as with connected components.
Scan the array of uptree nodes, counting the number of distinct roots of uptrees, and for each such root, insert into a hashtable (rootPixelID, count). Then scan the image and for each pixel, recolor it using progressiveColor(k) where k is the count value of the pixel's uptree root.
II.8. Implementation
Building on your solution to Part II, add a new menu item to your ImageComponents program. This will be another JMenuItem and should be given the variable name CCItem2. It should appear, in the running program, just under the item labeled "Compute Connected Components and Recolor", and the new label should be "Segment Image and Recolor".
Add to your code, in void handleCCMenu, after the place where you handle CCItem1:
if (mi==CCItem2) {
int nregions = 25; // default value.
String inputValue = JOptionPane.showInputDialog("Please input the number of regions desired");
try {
nregions = (new Integer(inputValue)).intValue();
}
catch(Exception e) {
System.out.println(e);
System.out.println("That did not convert to an integer. Using the default: 25.");
}
System.out.println("nregions is "+nregions);
// Call your image segmentation method here.
// It should have this signature: void segmentImageAndRecolor(int nRegions);
}
For your priority queue, the suggested implementation is to use Java's PriorityQueue class. To use this, import it from java.util.PriorityQueue. You should also create an inner class Edge that contains three components: endpoint0, and endpoint1 (both vertices that can just be int values corresponding to pixelID values) and the weight (which can be of type int). This Edge class should implement the Comparable interface (and so it must implement a method called compareTo(Edge e2). Your compareTo method should compare the current edge with the edge in the argument by looking at the weight, and return -1, 0, or 1, depending on whether the current edge's weight is less than, equal to, or greater than the weight of the edge in the argument.
II.9. Testing.
Test your program with the following images. Make the "donut2.png" image the default image that loads up when you start the program. The other images to try are "4sections.png" "gradients.png" and "ArezzoPiazza.jpg".
Here are some sample results for some of these images (courtesy of Johnson Goh, TA during A'14). For donut2.png with 9 seguments:

For 4sections.png with 4 segments:

For 4sections.png with 103 segments:

For 4sections.png with 202 segments:
For 4sections.png with 301 segments:

II.10. What to Turn In.
For the extra-credit portion of Part II, simply turn in your new file ImageComponents.java.
We will know whether or not you have implemented the extra-credit features according to whether
your code includes the method void segmentImageAndRecolor(int nRegions).
Version 1.0. Last updated Feb. 11 at 10:00 AM.