
Assignment A4: Hashing High-Volume Data -- Part I
Overview
In this assignment, we will be developing hashing functions and hashtables for an important type of data that is the most voluminous of all data in the internet: pixel data. We will be applying our hashing techniques to one of the big technical challenges connected with "big data" -- data compression.
Data compression is a big subject and there are many techniques, including JPEG compression (based largely on spatial frequency analysis of images using the discrete cosine transform), and LZW encoding to exploit statistical redundancy in a file. We will limit our data compression efforts in this assignment to the management of color information in images.
Hashing will help us analyze a population of data in an efficient way, which in turn will lead us to various choices in how best to represent and deliver the color information in an image.
Part I
Read this section and prepare your answers to all the questions (for example, Q1a, etc.) as either a .txt file or .pdf file. Turn it in by the Part I due date (Wednesday, February 3 at 11:59 PM) via Catalyst CollectIt.
I.1. Background for the application
A color is often represented in computer software using the "RGB" system. In this system, a triplet of numbers such as (255, 255, 0) represents a color. The first number tells how much red light is in the color. The second gives the amount of green, and the third gives blue. Each number can be as low as 0 (no light of that color) or as high as 255 (maximum amount of light of that color). So the tuple (another name for a sequence of numbers) just mentioned, namely (255, 255, 0), has the maximum amount of red and green, but no blue, and this color is yellow. Here are some more tuples and the colors they represent: (255, 0, 0) is red, (0, 255, 0) is green, (0, 0, 255) is blue, (0, 0, 0) is black, (255, 255, 255) is white, (255, 200, 200) is pink.
Once again, there is a physical interpretation of a member c=(r,g,b) of the set of colors we are considering. The three components, represented here as r, g, and b, specify amounts of light in each of three primary colors: red, green, and blue. Next let's consider what the set of possible colors is, using this scheme.
A 24-bit color tuple is defined as an element of the set
{0, 1, ..., 255}3
This is the 3-way cartesian product of the set of the first
256 natural numbers, with itself. (If you are not familiar with Cartesian products and tuples,
be sure to read or re-read section 5 of our third reading -- "mathematical background.")
Let us denote this set at C.
We sometimes call C the 24-bit color space.
Examples of elements in C are (0,0,0) and (127,255,15). Some tuples not in C include (0, -1, 0), (255, 255, 256), and (0, 1, 2, 3). The set C can be visualized as a 3D cube, as shown below (figure courtesy of Basler, AG).
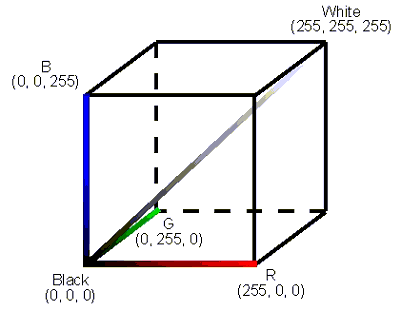
Q1a. Evaluate |C|. In other words, What is the cardinality of C? This is the same as the question, "how large is the set of 24-bit color tuples?"
The set C of colors offers a fairly complete palette of different colors and modern graphics cards and good LCD monitors can render each of these colors distinctly (or almost distinctly).
Q1b. Again considering the elements of C to be 3D points in a cube having diagonally opposite corners
at (0,0,0) and (255,255,255), what is the straight-line distance between
(255,0,0) and (254, 1, 1) ? For this, use the Euclidean distance between two n-tuples A and B,
denoted
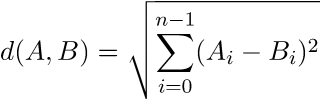
Q1c. However, the human eye doesn't always pick up on the subtle differences among all these colors, and there are many situations in which a smaller set of colors will suffice to render a scene pretty well from a human-perception point of view. There are a number of reasons to try to work in a smaller color space than C. For one, there can be storage space savings. For another, there can be network transmission time savings. Sometimes, there is even a desire for simplification or exaggeration of image features and that sometimes can go hand-in-hand with color-space reduction.
Certain image formats, such as GIF and PNG allow the representation of an image to use particular subspaces of C.
Suppose, in the interests of economy, all colors that fall within a certain subcube Q are to be represented by the color that lies at its center (or if the center's coordinates have fractional values, we use the floors of those values). What is the greatest distance between any two colors in Q? (Call this DQMAX and give an expression for DQMAX). Assume Q is given by the two diagonally opposite vertices (x0, y0, z0) and (x0 + d, y0 + d, z0 + d).
Q1d. What is the distance between black and white, where black = (0,0,0) and white = (255, 255, 255) ? (Call this DMAX).
Q1e. For a subcube Q of the color space C, give an expression, in terms of subcube size d, for the percentage P of DMAX represented by DQMAX. (Here DQMAX is the same as above -- the greatest distance between any two colors in Q.) For example, when x0 = y0 = z0 = 0, and d = 255, then P = 100 %.
I.2. Hashing functions for colors and blocks.
Before we get to our hashing functions, let's recall some basic Boolean algebra. Some of the most basic boolean operations are logical OR, AND, NOT, and Exclusive-OR. For example
0 AND 0 = 0 0 AND 1 = 0 1 AND 0 = 0 1 AND 1 = 1.
The Exclusive-OR operation is defined with the following:
0 XOR 0 = 0 0 XOR 1 = 1 1 XOR 0 = 1 1 XOR 1 = 0.
Any of these basic operations can be turned into so-called "bitwise" logical operators by processing corresponding bits from sequences of bits rather than just individual bits. This is described below.
Let c = (r, g, b) be an element of C. Define hash function h1 as follows: h1((r, g, b)) = r ^ g ^ b. We are using the caret symbol for bitwise exclusive-or. Note that the caret (^) in an expression such as P ^ Q denotes the bitwise exclusive-or operation in many modern programming languages, including Java, Python, C, and C++. To compute the bitwise exclusive-or operation for two integers A and B, express each in binary (base 2), line up the bits, and then perform, for each position, the logical operation of exclusive-or, obtaining a corresponding bit of the answer C. For the case A=255 and B=15, we have the following:
variable decimal binary decimal A = 255 = 1 1 1 1 1 1 1 1 B = 15 = 0 0 0 0 1 1 1 1 ------------------------------------------------- C = 1 1 1 1 0 0 0 0 = 240
For the hash function above, here is an example: h1((255, 15, 8)) = 248.
Q2a. Compute h1((192, 128, 15))
Q2b. Compute h1((255, 254, 253))
Q2c. Compute h1((127, 0, 255))
Q2d. What is the range of h1?
Define hash function h2 as follows:
h2((r, g, b)) = 1024 * r + 32 * g + b
Q2e. Compute h2((192, 128, 15))
Q2f. Compute h2((255, 254, 253))
Q2g. Compute h2((127, 0, 255))
Q2h. What is the range of h2?
Q2i. If we use a hashtable of size N = 521, and compute hashtable indexes from colors using i = h(c) mod N, then which hash function (h1 or h2) is likely to cause fewer collisions when hashing a list of colors? (Assume the number of distinct colors in the list is at most N.)
Q2j. Why?
I.3. GIF and PNG palettes.
The GIF and PNG formats offer a variety of features for the efficient representation of digital images. They are both particularly good at representing synthetic images such as graphic designs, logos, and images with sharp boundaries and limited numbers of colors.
A typical GIF or PNG image has two essential parts:
1. a color table with 2t entries. Thus, the table size must be a power of 2 with t in the range 1 to 8. Common values of t are 1, 2, 4, and 8. Each entry in the table is a 24-bit color tuple.
2. pixel data consisting of a 2D array of integers in the range {0, 1, ..., 2t-1}.
Encoders and Decoders
There are two kinds of software for working with images such as these: encoders and decoders. A browser typically contains decoders that are used to process a GIF or PNG image and determine the actual color values for all the pixels in the image, so that they can be drawn on the screen. An image editing program contains both decoders and encoders. The encoders are used to translate the actual pixel data into the format of GIF or PNG as specified.
There are two key steps in encoding:
1. determining an appropriate color table (called a palette) and
2. mapping the pixel values from the image into color table entries.
Each of these can be done in many ways. For example, it could be decided by the author of the encoder that a standard color palette should always be used, even if it is not optimal for the image that is to be encoded. This would speed up the encoding process, for one thing. Alternatively, a careful analysis of the colors in an image could be performed in order build a palette that is representative of the colors in the image.
The mapping of pixel values from the image into the color table can be done easily, if there is actually a color table entry for every color occuring in the image. If not, then each pixel's value should be mapped to the index of the color in the table that matches it most closely.
As we will see, hashing can be used in each of these two steps. But first, let's do some simple examples of palette construction and encoding of the pixels.
Example 3.1:
We scan the image below starting with the top row, moving left to right. Whenever a new color is found, create a new color table entry.
Image as RGB Color table T
(255,0,0), (0,255,255), (127,127,127), 0: (255,0,0)
(127,127,127), (0,0,0), (254,0, 0), 1: (0,255,255)
(0,255,255), (255,0,0), (127,127,127), 2: (127,127,127)
(0,0,0), (127,127,127), (0,255,255) 3: (0,0,0)
4: (254,0,0)
Now we encode the pixels of the image using the table T getting a new array P:
P: Image as color indices 0 1 2 2 3 4 1 0 2 3 2 1
Q3: Build the color table T and the image P as color indices for the following Image given with RGB triples:
(100,200,0), (100,200,0), (50,50,50), (128,128,128), (50,50,50), (100,200,0), (255,255,255), (100,200,0), (255,255,255), (1,2,3), (255,254,0), (50,50,50)
I.4. The "Popularity algorithm" for color table creation.
This method starts by conceptually dividing the color space C into many small blocks of size s by s by s. Typically s = 4 or s = 8.
For a given 24-bit color tuple c= (r,g,b),
we can determine which block it belongs in by dividing:
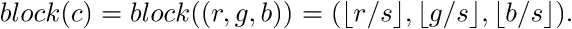
For example, taking s=4, block((255, 127, 32)) = (63, 31, 8).
Q4a: Compute the blocks for each of the 12 pixels of Exercise Q3. Assume s = 8 for this exercise.
We proceed by creating a hash table, H for storing pairs of the form ( B, w ), where B is a block and w is an integer weight.
We scan through all the pixels of the source image I and for each pixel p:
let c = color(p)
let B = block(c)
if H contains a pair with block B as key,
let w = H.get(B)
w = w + 1
H.put(B, w)
else:
H.put(B, 1)
By this point, we have a hashtable full of blocks and their counts.
Q4b. Draw a hashtable with capacity 16. Using the hash function h0((x, y, z)) = x, and the linear probing policy for collision resolution, insert each block from your answer to the previous question into the hashtable, and associate with each block, its number of occurrences (its count). If a block is not in the hashtable, we assume its count is 0. Your hashtable drawing should consist of a grid with 16 rows and 3 columns. The first column gives the index of the hashtable position; the second column gives the block itself, and the third column gives the count of occurrences.
Next we make a list L of the blocks and their counts by getting all of the pairs out of the hashtable.
Now sort L by the weight values, so that the w values are in nonincreasing order. The largest is first.
Assuming the palette should have U entries,
choose the first U elements of L, and call this LU.
For each block B in LU,
compute the representative color: the color in the center of the block.
representative(B) = representative((Br, Bg, Bb)) = (s * Br + s/2, s * Bg + s/2, s * Bb + s/2)
The color table consists of the U representative colors, in an array T.
Q4c. Let U = 4. Give the resulting array T, based on your answer to exercise Q4b. When you select the U blocks of greatest w values, break ties by taking the blocks closer to the beginning of the hashtable. (This is arbitrary and an implementation can break ties in any consistent manner.)
I.5. Encoding the Pixel Array
To determine the color table indexes to use for each pixel, there are two approaches: slow-and-simple, or fast.
Slow-and-simple: For each pixel, find the color table entry that minimizes the (Euclidean) distance between the pixel color and table color. Store the index of that color into the output pixel array P.
Q5a. Determine the 12 index values using the Slow-and-simple method for the example from Q4a-c.
Fast: First, create an index that maps each "populated block" to its best representative. Go through the list L of block-weight pairs.
For each (B, w) pair:
Compute its representative color rc as the color of the center of block B.
Scan the color table T to find the index i of the closest color to rc.
In hashtable H, replace the entry (B, w) by (B, i).
Now the hashtable represents a dictionary that maps blocks to color table entries. Now that we have this dictionary, we can easily look up what color table index to use to encode a pixel p.
Scan the source image and for each pixel: Let c be the color of the pixel. Let B = block(c). Let i = H.get(B). Store i in the output array P as the color table index for this pixel.
Note that the Fast algorithm might not produce exactly the same output array as the Slow-and-simple method, because the distance comparisons are done using block representatives rather than original pixel colors.
Q5b. Determine the 12 index values for the array P, with the same 4-element color table T, but using the Fast method.
I.6. Decoding
Decoding is not only part of the encoding-decoding chain, but it is also useful to evaluate the quality of the encoding.
Decoding from the representation computed above is straightforward:
Allocate a new image array (in Java, typically a BufferedImage object). Scan through the indexed color array (output of encoding, called P above), looking each index up in the table T to get the corresponding color. Store the color information into the new image array.
Typically, there will be a loss of information due to the limitation on the number of colors allowed in the table. The loss will be more apparent if U is small relative to the number of distinct colors in the image. For example, if the image has 9999 distinct colors in it, but U=16, then many colors may be substantially "off" in the resulting indexed color version.
Turn-in
Turn in either a .txt file or a .pdf file with your Part I answers through our Catalyst CollectIt dropbox. Part I of this assignment is due Wednesday, February 3 at 11:59 PM. Late penalties apply (see the policies page for details).
Grading Rubric
In this assignment, you can earn 100 points Part I is worth 30 points, and Part II is worth 70 points.
Part I. (30) Q1: 5; Q2: 10; Q3: 5; Q4: 5. Q5: 5.
Version 1.0. Last major update Tuesday, January 26 at 10:19 PM.