Ready for some fancy stuff? This time around we are going to create the .dat file from scratch. We are going to synthesize the sound (create the second column of the .dat file) using a method called the "Karplus-Strong" algorithm. This algorithm depends on queues. So before we get started, you must first implement a queue.
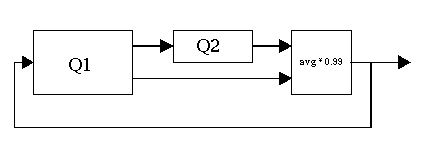
What we want to do is create two queues, Q1 and Q2.
Into Q1, we will enqueue n random numbers between -1.0 and 1.0.
Into Q2, we will enqueue a single 0.0. At every stage of the algorithm,
this is what we do (in pseudocode):
a = Q1.dequeue();
b = Q2.dequeue();
c = 0.99 * average(a, b);
Q1.enqueue(c);
Q2.enqueue(a);
output(c);
... and we repeat this m times. The following block diagram of the algorithm may make it clearer what is going on:

This program should be called ks.
The basic idea behind the algorithm is that Q1 is initially filled with a "burst" of sound n samples long. We want to keep sending out the same burst of sound over and over again. That's why we enqueue the output back into Q1, creating a "feedback loop." But we want the sound to get softer each time it goes through the loop so we multiply it by that constant 0.99 each time it goes through. Okay, that's fine: Q1 is a big feedback loop through which we are putting an initial burst of sound over and over again, making the sound slightly softer each time, but what is the point of Q2? Q2 makes it so that every time we output a number, it is averaged with the number that came before it. This "smooths out" the guitar string sound over time, reducing the timbre of the sound with each period.
One more question, what are n and m? Well, n is the number of samples in the loop. If S is the sample rate, then S / n is the number of times the sound repeats itself per second. This is the so-called "frequency" of the sound, and it is what we hear as pitch. Double the size Q1 and you will halve the frequency, lowering the pitch by one octave. Similarly, halve the size of the queue and you will increase the pitch of your guitar sound by one octave. Finally, m is the total number of samples in the output file. This implies that m / S is the number of seconds in the output file.
After you create the .dat file, convert it to a .wav with sox and listen to it! There is a lot of cool stuff to play around with here. Change the size of Q1 (or Q2!). What happens? Change the dampening constant from 0.99 to something else. What happens?
When you are done, turn in a copy of your source code. Your compiled source code should create a file with 5 seconds worth of "guitar sound" at a sample rate of 44.1kHz , at a frequency of 220Hz, and with a dampening constant of 0.99 (as in the pseudocode example).