CSE
373 Data Structures 09wi, Homework 4
Due at
the BEGINNING of class, Friday, 2/13/09
1) Binary Min Heaps: For both questions
draw BOTH a picture of the tree structure AND what the final array looks
like. You do not need to show
intermediate values of the array structure.
Showing intermediate pictures of the tree structure is also not required
but may allow some partial credit to be assigned. Please circle your final answer to both
questions.
a) Show the result of inserting the following values in this order into a binary min heap using insert: 10, 12, 1, 14, 6, 5, 8, 15, 3, 9, 7, 4, 11, 13, 2
b) Show the result of using Floyd’s buildheap method (as described in class and in the book) to create a heap out of values assuming you are given them in an array laid out in the order given above.
2) Binary Min Heap Algorithms: : For both of these problems, for full credit your solution should be the most efficient possible – perhaps in the worst case they might need to examine every element in the heap, but in general this should not be the case. You may assume an array layout of the binary min heap as discussed in lecture and in the book. You also may assume that your algorithm has direct access to the heap array (it does not need to manipulate it just by using the standard heap operations – insert, deletemin, findmin, etc.). Your algorithm should not modify the heap (just like a findmin does not modify the heap) – or at the very least, if it does, it should put it back identical to how it was before you started.
a) Give pseudo code for an efficient algorithm to find the maximum value in a binary min heap. What is the worst case big-O running time or your algorithm?
b) Give pseudo code for an efficient algorithm to find all nodes less than a given value in a binary min heap. Your algorithm should just print out the values it finds. What is the worst case big-O running time of your algorithm?
3) Skew Heaps: Show the result
of inserting values in this order into an initially empty skew heap: (1, 2, 6,
3, 4, 8, 7, 5, 9, 10, 11)
4) Leftist Heaps:
Below are two leftist heaps. Show the result of merging them together using the algorithm we discussed in class. You are only required to show the final tree, although if you draw intermediate trees, please circle your final result for ANY credit.
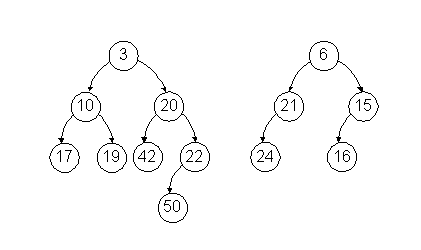
5) Disjoint Sets: Consider the set of initially unrelated elements 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
a.)
Draw the final forest of up-trees that
results from the following sequence of operations using on union-by-size.
Break ties in size by keeping the root of the set the first argument belongs
to as the new root. Perform a find
(without path compression) if you need to find which set an element belongs to (and then union the two sets as you normally would).
Union(0,3), Union(3,4), Union(7,9), Union(9,3), Union(7, 14), Union (6,8),
Union(6,0), Union(12,6), Union(1,12), Union(11,5), Union(7,11).
b.) Draw the array representation of your answer above. Use the value -1 to represent a root.
c.) Draw the new forest of up-trees that results from doing a Find(9) with path compression on your forest of up-trees from (a).