Programming Assignment 3: Graph Matching

Due: Friday March 12 at midnight

ReadGraph.java

some Java code to help you read a graph from a file, also check out Sample.java

ReadGraph.c

some C++ code to help you read a graph from a file, also check out Sample.cpp

graphs.zip

several graph data files for testing your program

pictures.zip

pictures of the above graphs, useful for debugging

c4.gif

replacement picture of graph c4

Overview

This project is related to the problem of recognizing objects in images. Given a known object and a new image, we want to determine whether or not that object is present in the image. Both the image and the object are represented as graphs, where a node corresponds to a region of pixels and the edges correspond to adjacencies between regions.

Suppose we have a model graph G_M (the object) and an image graph G_D (the image). With this representation, the problem reduces to: determining if there is a subgraph of G_D isomorphic to G_M (for perfect matches).

Suppose G_M has vertices {1,2,3,...,n₁} and G_D has vertices {1,2,3,...,n₂}, where n₁ <= n₂. Then, a mapping f(v) can be expressed as a set of pairs {(1,i₁),(2,i₂),(3,i₃),(n₁,i_n1)} such that every vertex in G_M is mapped to exactly one vertex in G_D. For a subgraph isomorphism, the number of edges (u,v) in G_M for which (f(u),f(v)) is not an edge in G_D MUST BE ZERO. Your program will find all subgraph isomorphisms from the model graph G_M to the image graph G_D.

What You Need To Do

Write a program that can be executed from the command line with

	Match gmfile gdfile 

for C++, or

	java Match gmfile gdfile 

for Java. The gmfile and gdfile arguments should be the names of two files that contain graphs (see the format specified below).

Details

Reading the Graphs

You will need to read the graphs from two files, one for each graph. The graphs are undirected, and the nodes are labeled between 1 and the number of nodes, which is specified in the file. The file format is as follows:

	GRAPH NAME (a string)
	N (the number of nodes, an integer)
	M (the number of edges, an integer)
	U1 V1 (two node labels specifying an edge, both integers)
	U2 V2
	U3 V3
	  .
	  .
	  .
	UM VM

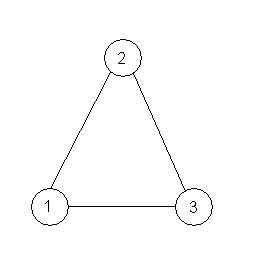
For example, a graph file might look like:

triangle 3 3 1 2 1 3 2 3

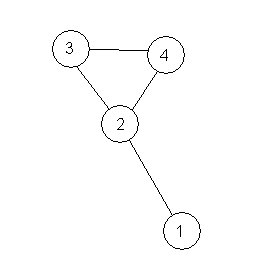
or

kite 4 4 1 2 2 3 2 4 3 4

Output

Suppose the above two graphs are stored in files triangle.graph and kite.graph. Then, the command

	Match triangle.graph kite.graph 

should output

	ISOMORPHISM: (1,2),(2,3),(3,4)
	ISOMORPHISM: (1,2),(2,4),(3,3)
	ISOMORPHISM: (1,3),(2,2),(3,4)
	ISOMORPHISM: (1,3),(2,4),(3,2)
	ISOMORPHISM: (1,4),(2,2),(3,3)
	ISOMORPHISM: (1,4),(2,3),(3,2)

If there are no isomorphisms, output NO ISOMORPHISMS on a separate line with no punctuation.

What To Turn In

You should turn in the following:

• a readme file describing what you did
• all of your code
• the output you get for each of the following invocations of your program:
  • Match small_house.graph big_house.graph (2 expected.)
  • Match c4.graph small_house.graph (16 expected).
  • Match k4.graph big_house.graph (0 expected).

For your own amusement, you can try

• Match k5.graph usa.graph

All of the above files are included in the graphs.zip archive. You can use the triangle and kite graphs to help debug your program.

And Remember.....

• Your java class which contains the main method must be named Match
• Your program must take in two input filenames in the same order as stated earlier in this document. You can refer to your earlier projects or the sample file given to you with this project to figure out: how command line arguments are passed.
• Please make sure you follow the output format as closely as possible.

Some sample outputs for your comparison