CSE 370 Solution Set #5
Spring 1999
Total Points 20
1) Katz 4.18a,b Points: a:0, b:1
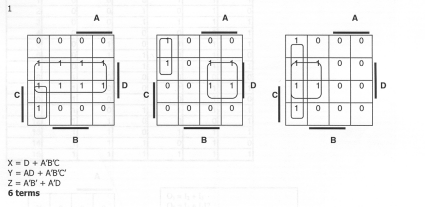
Part A- X = D + A'B'C Y = AD + A'B'C' Z = A'B' + A'D

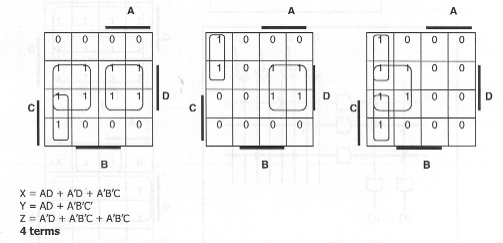
Part B - Group the K-maps as below. Results in an expression that has only 4 total unique terms.
X = AD + A'D + A'B'C Y = AD + A'B'C' Z = A'D + A'B'C + A'B'C'
2) Katz 4.21 - 3 points:
a.
| I3 | I2 | I1 | I0 | | | O(1) | O(0) |
| 0 | 0 | 0 | 0 | X | X | |
| 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
Part B) O(1) = I2 + I3
O(0) = I3 + I1 I2'
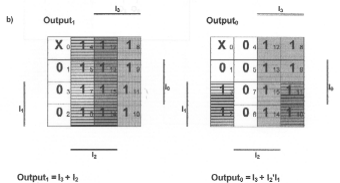
Part C)
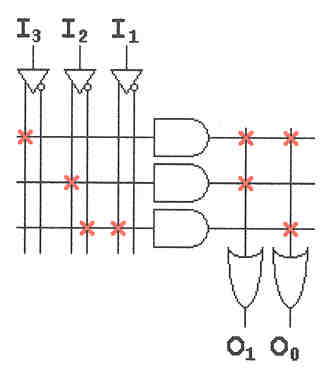
3) 5 Points:
Part A: Here is the truth table. Note both +0 and -0 map to 0, which is logical, but not required for this HW.
| I4 | I3 | I2 | I1 | I0 | | | O3 | O2 | O1 | O0 | Err |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | x | x | x | x | 1 | |
| 0 | 1 | 0 | 0 | 1 | x | x | x | x | 1 | |
| 0 | 1 | 0 | 1 | 0 | x | x | x | x | 1 | |
| 0 | 1 | 0 | 1 | 1 | x | x | x | x | 1 | |
| 0 | 1 | 1 | 0 | 0 | x | x | x | x | 1 | |
| 0 | 1 | 1 | 0 | 1 | x | x | x | x | 1 | |
| 0 | 1 | 1 | 1 | 0 | x | x | x | x | 1 | |
| 0 | 1 | 1 | 1 | 1 | x | x | x | x | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | x | x | x | x | 1 | |
| 1 | 1 | 0 | 1 | 0 | x | x | x | x | 1 | |
| 1 | 1 | 0 | 1 | 1 | x | x | x | x | 1 | |
| 1 | 1 | 1 | 0 | 0 | x | x | x | x | 1 | |
| 1 | 1 | 1 | 0 | 1 | x | x | x | x | 1 | |
| 1 | 1 | 1 | 1 | 0 | x | x | x | x | 1 | |
| 1 | 1 | 1 | 1 | 1 | x | x | x | x | 1 |
Part B:
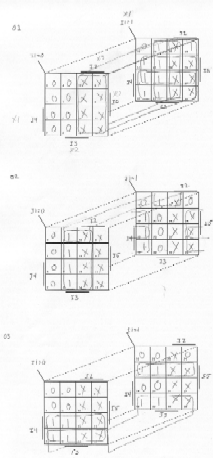 |
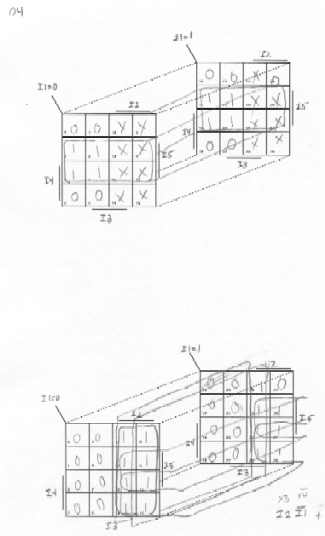 |
O3 = I3 + I4 I2 + I4 I0 + I4 I1
O2 = I2 I1' I0' + I4' I2 + I4' I2' I1 + I4 I2' I0
O1 = I4' I1 + I1 I0' + I4 I1' I0
O0 = I0
Err = I4' I3 + I3 I2 + I3 I0 + I3 I1
Part C: This was done just as in the smaller problems, but the picture of this was either too big or too fuzzy to be of any use. If you have any questions just ask Grant.
4) 0 Points:
Full Adder Sub-Circuit
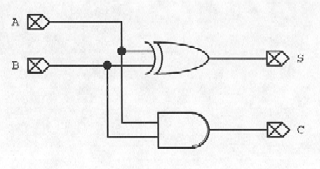
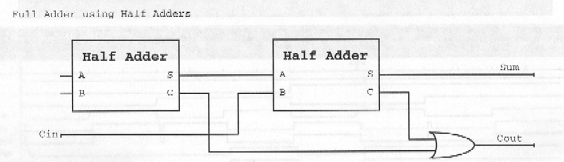
Full Adder Using Half Adders
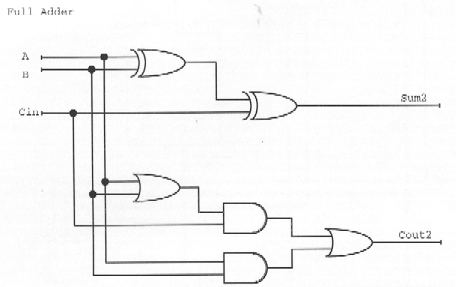
Full Adder
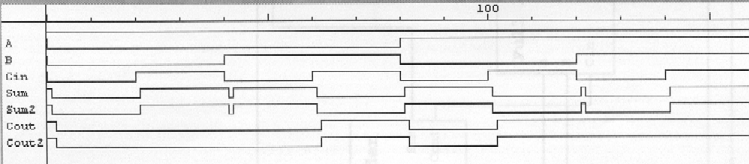
Sample Wave Form - Sum is from the Circuit using half adders, Sum2 is from the pure Full Adder.
5) 2 Points:
Four Bit Ripple Carry Adder
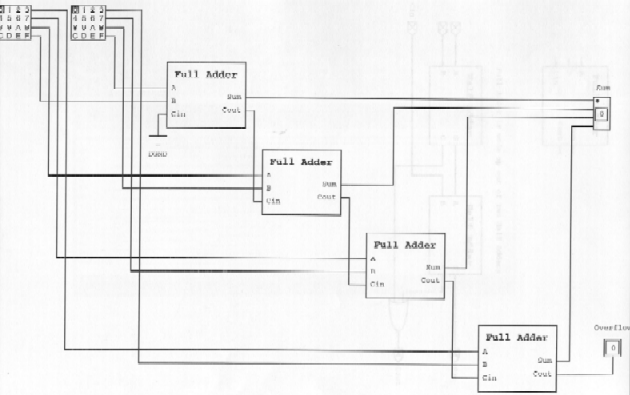
The timing of the ripple carry adder should reflect the carry bit propagating down. This was most evident in the input combination 0000 + 1111 -> 0001 + 1111 because the carry bit must propigate all the way down, making the timing wave form look like a ladder. If your bit only propigated through one step it is likely that the high and low order bits were reversed.
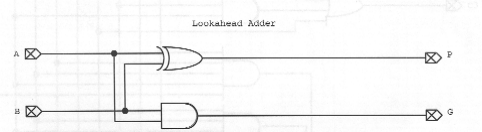
6) 5 Points: You didn't have to break down the circuit like this, but this
is good way to do it.
Look ahead adder unit - Generates Propigate and Generate Signals
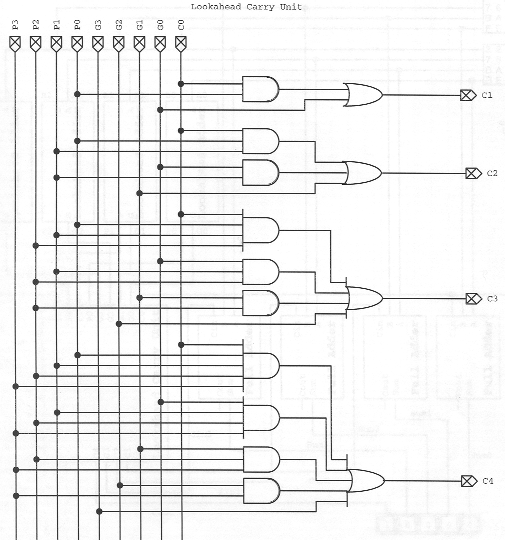
Lookahead Carry Logic Unit
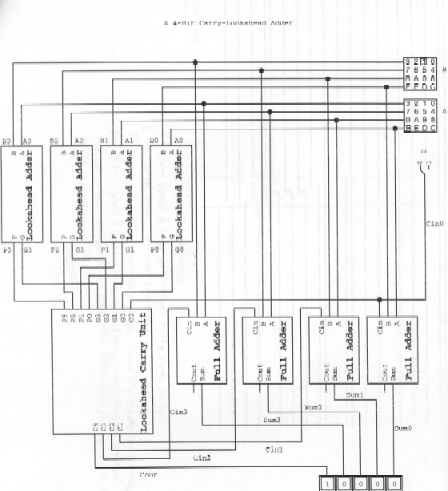
Top Level Schematic using the look ahead units. It is not necessary to use the full adders (the Cout are not used), but this is fine because it is specified this way in the problem.
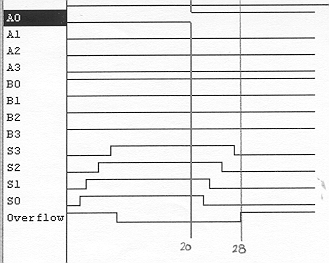
Here is a rough display of what the timing diagram should look like. The Carry-Lookahead adder is very fast because it has no delay from the signals rippling though.

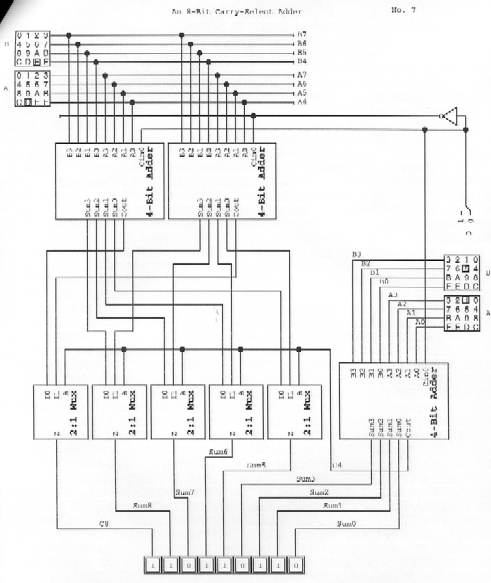
7) 4 Points total:
A 2:1 mux which is useful for this problem
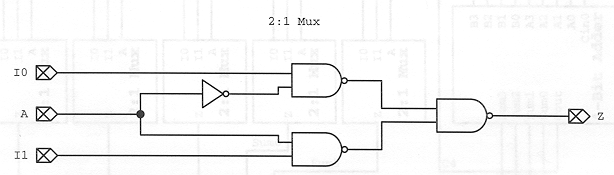
And the entire circuit. The upper four bits of each number are fed through the muxs and selected based on the Cout of the lower four bits