1) 0 Points:
Weekly assignments are worth 40% of your final grade. Any relevant question you'd like to see on the evaluation is fine.
2) 0 Points:
Yes I have an NT account, can login, I'm familiar with the environment (I should be after 3 years), and I'm subscribed to the mailing list.
3) 4 Points:
a. 2^5+2^4+2^1+2^0 = 51
b. 6*8^1+3*8^0 = 51
c. 3*16^1+3*16^0 = 51
d. 2^6+2^5+2^1+2^-1+2^-3 = 98.625
4) 4 Points:
a. Succesively divide by 2 and look at the remainders.
answer = 11010100 (unsigned binary)
b. Here, since the base is a power of 2, we can group digits. So each octal digit represents 3 binary digits. 3 = 011 & 7 = 111, so just concatenate these in the proper order of significance.
answer = 011111 (unsigned binary)
c. Break the number up into 17 & 0.4375. Convert 17 by succesively dividing by 2 and looking at the remainders, and convert 0.4375 by succesively multiplying by 2 and looking at the whole number carries.
answer = 10001.0111 (unsigned binary)
d. Here, since the base is another power of 2, we can group digits. So each hex digit represents 4 binary digits. D = 1101 & 2 = 0010 & C = 1100 & 3 = 0011, so just concatenate these again in the proper order of significance.
answer = 1101001011000011 (unsigned binary)
5) 4 Point:
a. 50 (octal)
b. 10010 (unsigned binary)
c. 01011 (unsigned binary)
d. 101011 (unsigned binary)
6) 4 Points:
a. 101111 (signed magnitude binary)
b. 110001 (2s complement binary)
c. In 8-bit 2s complement the smallest number is -128 and the largest is 127
d. Sign extend the most significant bit = 11111001 (2s complement binary)
7) 2 Point:
-6 is represented as 1010 in 4-bit 2s complement binary. Assuming that a 4-bit 2s complement number is written as X4X3X2X1 then this translates to a boolean expression of X4X3'X2X1'
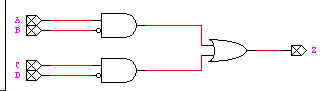
8) 2 Points:
Here is an example DesignWorks circuit solution.