CSE 370 Laboratory
Assignment
Introduction to
Registers
Assigned: Monday, February
15, 2010
Due: End of Lab Section
Objectives
The
objective of this lab is to introduce you to edge-trigged D-type flip-flops as
well as linear feedback shift registers. You can refer to Chapter 6 of your
textbook Contemporary Logic Design for more information. Typically for
flip-flops and registers you use a clock signal, however, a typical clock
signal such as ones provided one your hardware are far too fast for the LED
changes to be visible to the unaided eye – they are just too fast. Therefore, we will simulate clock pulses
throughout this lab by using a button. Even though a button is not a regular clock,
what happens when the button is depressed is roughly the same; a pulse is sent through
the circuit with both negative and positive edges that will be used to trigger
flip-flops. You can consider button pushing to be a very slow irregular clock
signal – but one that you can control.
Before You Begin
If
you followed the instructions properly in the previous lab, when you turn on
your board for this lab you will notice that the original program loaded on the
FPGA is still there, which means you can make use of the switches, LEDs and buttons
directly connected through the input/output connectors on the board. If you
find that this is not the case, call over a TA and they will assist you in
restoring your old settings. Of course, by now, you are well versed in the
FPGA, which means you can undertake the task of rerouting the switches, LEDs
and buttons yourself if you choose to.
Part 1: D
Flip-Flops
Tasks:
- The '74 package has 2 D
flip-flops. You'll note each flip-flop has a data input, D, a clock input,
CP, two outputs, Q and Q', and two additional inputs, SD and CD. These
last two are active-low (they have an effect when 0 and none when 1)
asynchronous set and clear inputs. Insert the '74 chip into your
breadboard and connect the D input to one of the switches, a button to the
clock input, and Q to one of the LEDs. Make sure to also connect SD and CD
to a logical 1, such as VDD to ensure that they aren’t triggered for this
first part.
- Spend some time experimenting with the flip-flop.
Toggle your switch so that a value of 1 is on the D input to your
flip-flop and press the button. What happens to the LED you connected to
Q? Try changing the value of D and push the button again. Try changing D
back and forth while not pushing the button wired up as your clock. Note
how Q only changes after you press the push button. This is a synchronous
flip- flop, changes in the output only occur after a rising clock edge
(positive edge-triggered, this occurs every time you press the button down
because the button generates a positive pulse). You can surmise that if
you had a faster clock, such as someone pushing the button for you very
quickly, whenever you flipped the switch the effect would appear almost
instantaneously, depending on the speed of the clock.
Clock Skew
We will experiment with clock skew by using even numbers of inverters to delay the propagation of your simulated clock. Wire up the second D flip-flop on the ’74 package. Use your output from the first flip-flop as the input for the second flip-flop. Also, wire the same button to both clock inputs. Your circuit is now a 2-bit shift register. Try shifting in some bits; because both flip-flops’ clocks are in sync, it will function as expected. Now, add a ’04 inverter package to your breadboard and wire together two of the inverters in a chain. Connect the clock button to the clock input of the first flip-flop and to the input of the first inverter in the chain. Connect the inverter output at the end of the inverter chain to the clock input of the second flip-flop. The two inverters’ delay will now skew the clocks received by the two flip-flops. See if your shift register still works. Does it still work if you add two more inverters to the inverter chain, for a total of four inverters; skewing the second clock signal even further? What does this mean about the relationship between the delay of the inverters and the timing constraints of the flip-flops? Show your TA a case where the two-bit shift register functions as expected and a case where it does not work due to clock skew.
- Now it is time to experiment with the asynchronous set
and clear inputs. Connect these to switches instead of VDD (logic 1) to
which they were previously connected. Make sure the switches are initially
set to output a 1. Now, set the value of Q to 0 using the D input and the
push-button. Flip the SD switch. What happens? Did you have to press the
push-button? Asynchronous input take effect immediately, without waiting
for the next clock edge. Repeat the experiment with CD instead of SD. Try
setting both SD and CD to 0 (set and clear at the same time), which dominates?
Does the flip-flop set or clear?
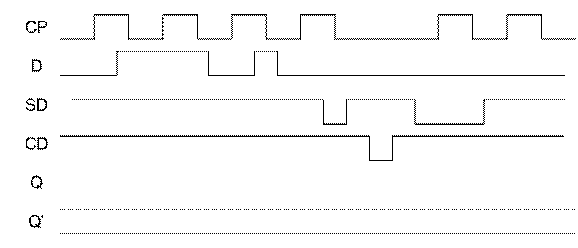
- Copy the timing diagram below onto your own piece of
paper and fill in the rows for Q and Q' for the first check-off.
Part 2: Linear
Feedback Shift Registers (LFSRs)
LFSRs
have an interesting property that a particular function of a subset of the
outputs will cause the shift register to cycle through a maximal length
sequence of output values. In the case of a 4-bit shift register, a maximal
length sequence would have 15 (16 - 1, the all-zero pattern is not counted)
different outputs. If the function can be implemented efficiently, this
capability can be much easier to implement than building a binary counter
(recall that a binary counter is a specialized adder but still has a long
carry-chain of larger and larger gates).
Binary counters with a large number of bits can be quite expensive in terms of
the logic they require. On the other hand, LFSRs with maximal sequences can be
made with input functions that are low fan-in (depend on only a few of the
register's outputs) and do not have a carry-chain. This makes LFSRs very
attractive when we need to count to large values but don't care about what the
patterns are (that is, they don't have to be consecutive binary numbers).
Variations of LFSRs are often used as random number generators as well -
consecutive output patterns can be made to look quite different and are
uniformly distributed over the space of all possible patterns. You can read a
lot more about LFSRs at New
Wave Instruments: each of these sites includes a complete list of functions
that will generate maximal sequences for any number of bits from 4 to 32 and
beyond.
For example, a 4-bit LFSR with maximal length sequence will have the following
function: D1 = Q4 xor Q3. A larger 8-bit LFSR with D1 = Q8 xor Q7 xor Q6 xor Q1
will have a 255 pattern long maximal sequence. Interestingly, a 32-bit LFSR can
also have a maximal sequence (232-1 patterns long) with a function
of only 4 output variables, namely, D1 = Q32 xor Q31 xor Q30 xor Q10.
Tasks:
- Wire up your '377 octal D-FF
to form a 4-bit shift register. Connect the four FF outputs to four of the
LEDs. Connect the output of a 2:1 multiplexer to the first input with a
switch connected to the mux's control input. The two mux inputs should be
the value of another switch and the last output of the shift register (the
fourth bit). Verify the operation of your shift register by setting the
input to come from the switch. Go through a few clock cycles shifting in
different values. Make sure to tie the enable input of the '377 to a value
rather than leaving it floating as it may not function properly without a
valid logic level on that input. Show your shift register to a TA for the
first part of the second check-off.
- Shift the pattern 1, 1, 0, 0 into your shift register.
Flip the input mux switch so that the last output is now fed back into the
input. Go through a few clock cycles by pressing the button you have wired
up as your "clock". You should see your pattern shifting in a
circular pattern through the register. How many different patterns are
there in all before the output pattern on the LEDs repeats itself?
- Invert the value of the last bit being fed back around
before it goes into the mux. Repeat the previous task with this new
configuration. How many different patterns do you see?
- Remove the inverter and replace it with an XOR gate
with the 4th and 3rd FF outputs as its inputs. Connect the output of this
XOR gate to the input mux of the shift register. This is a 4-bit LFSR.
Begin by shifting in zeros into your shift register (use the switch input
to the mux). Now flip the mux to select the output of the XOR gate to be
the input. Go through a few clock cycles. Does the pattern change? Now,
shift in all ones (instead of zeros) to set up the shift register and then
go through a few clock cycles. How many patterns do you go through before
they begin to repeat? Is this a maximal sequence? Show your LFSR in
operation to one of the TAs. Try different taps instead of 4th and 3rd,
for example, 4th and 2nd. How many different patterns does this
configuration generate? Demonstrate your LFSR to the TA to second part of
the second check-off.
OPTIONAL: Finite State Machines in Verilog
You
have seen some diagrams of finite state machines (FSMs) in class. This tutorial
will show you how to take a diagram of a simple FSM and convert it to a Verilog
description. This is optional because it
may be a tool you will find useful in later assignment. However, it will not be required that you use
the state diagram tool.
Task:
- Complete the tutorial
on how to describe Finite State Machines in Verilog.
Lab
Demonstration/Turn-In Requirements
A TA
needs to "Check You Off" for each of the tasks listed below.
- Demonstrate the effect of clock skew on your register
in Part 1, Task 2.
- Show your completed timing diagram from Part 1, Task 4.
- Demonstrate a.) your 4-bit shift register from Part 2,
Task 1 and b.) LFSR from Part 2, Task 4.
Comments
to: cse370-webmaster@cs.washington.edu