CSE370 Laboratory Assignment 6
Introduction to Registers and LFSRs
Distributed: Monday, February 13, 2006
Due: End of Lab session
Objectives
In Part 1 of this laboratory assignment you get to know edge-triggered D-type
flip-flops. You will be using the '74 component in your kit (see
map). This will be the first time you use a clock signal and
learn about both synchronous and asynchronous inputs to the flip-flop.
D-type flip-flops are the primary sequential logic device and we will be using
them throughout the remainder of the quarter.
In Part 2 we will construct a larger sequential system, namely, a new type of
shift-register. We will primarily use the '377 octal D-FF with input
enable (see map) in your kit.
NOTE: This laboratory assignment has two checkoff points.
XLA5 Prototyping Board
To do this laboratory assignment, as well as all the future ones, you will need
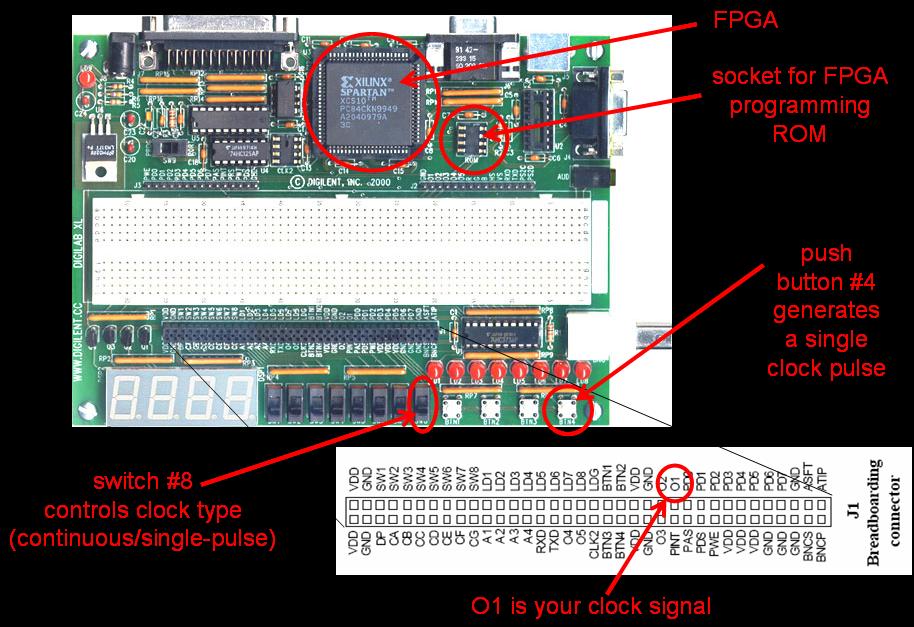
a periodic clock signal. We have programmed the large FPGA on the XLA5
board to provide you a convenient clock that will make it easier for you to
debug your circuits. The figure below shows the FPGA as well as the
socket that will hold the programming ROM for the FPGA. The programming
ROM holds the configuration file for the FPGA - the collection of 0s and 1s
that will configure the FPGA to have the functionality we desire. This
program was derived using the Aldec tools.
Here is the basic idea for the clock generated we've constructed for you.
Rather than having you deal exclusively with a crystal-generated clock signal
that runs continuously, we've programmed the FPGA to deliver a more versatile
clock signal. Using switch #8, you can set the clock into one of two
modes (LED #8, the right-most LED follows the value of this switch). In
the first mode, with the switch set to 1 and LED #8 on, the clock runs
continuously with a nice slow frequency of 1.537KHz (or a period of 650
microseconds). In the second mode, with the switch set to 0 and LED #8
off, there is a single clock pulse whenever push button #4 is pressed.
This mode allows you to single-step your sequential circuit. The width of
the clock pulse is the same as when the clock is running continuously
(nominally, high for half a period or 325 microseconds). This clock was
chosen to be slow enough that we would not have to be concerned with the delay
of the logic during the laboratory assignments.
Once you are done debugging, you can flip the switch into continuous clock
mode. The figure below provides the details.
Tasks- Part 1
Note: You can fill in the timing diagram in step 4 while doing steps 2 and 3.
1. The '74 has 2 D flip-flops in one package (see map). You'll note each flip-flop has a data input, D, a clock input, CP, two outputs, Q and Q', and two additional inputs, SD and CD. These last two are active-low (they have an affect when 0 and none when 1) asynchronous set and clear inputs. Insert the '74 chip into your protoboard and connect the D input to one of the switches, the clock input to O1, and Q to one of the LEDs. Make sure to also connect SD and CD to a logic 1 (VDD will do).
2. Spend some time experimenting with the flip-flop. Set the clock switch to pulse mode. Set the D input to a value, push button #4 to generate a clock pulse. What happens to the LED you connected to Q? Try a different value of D and push the button again. Try changing D back and forth while not pushing button #4. Note how Q only changes after you press the push button. This is a synchronous flip-flop, changes in the output only occur after a rising clock edge (positive edge-triggered). Now repeat this in continuous clock mode. What is the difference?
3. Now it is time to experiment with the asynchronous set and clear inputs. Connect these to switches instead of the logic 1 they were previously connected to. Make sure the switches are initially set to output a 1. Now, set the value of Q to 0 using the D input and the push-button. Flip the SD switch. What happens? Did you have to press the push-button? Asynchronous input take affect immediately, without waiting for the next clock edge. Repeat the experiment with CD instead of SD. Try setting both SD and CD to 0 (set and clear at the same time), which dominates? Does the flip-flop set or clear?
4. Fill in the timing diagram below, showing the values for Q and Q’.

5. The last task is to create a simple four-bit shift register, using two '74 packages (4 flip-flops). Wire up the second flip-flop and set its D input to be the Q output of the first flip-flop. Continue with the second '74 package, so that you have four flip-flops connected sequentially. Connect four LEDs to the Q outputs of the four flip-flops. Set the D input of the first flip-flop to 0 and push button #4 several times. Make sure you've connected all the CD and SD inputs to logic 1 (failure to do this will cause your flip-flops not to work as expected as an unconnected pin may be interpreted as a 0 causing the flip-flop to set or clear). Now, set the first D input to 1 and push button #4 once, then more. What do you observe on the LEDs? Convince yourself that the circuit is functioning as a 4-bit shift register and demonstrate this to the TAs to be checked off for Part 1.
Linear Feedback Shift Registers (LFSRs)
A linear feedback shift register is a special kind of shift register whose
single data input is a function of the shift register's outputs. They
have an interesting property that a particular function of a subset of the
outputs will cause the shift register to cycle through a maximal length
sequence of output values. In the case of a 4-bit shift register, a
maximal length sequence would have 15 (16 - 1, the all-zero pattern is not
counted) different outputs. If the function can be implemented
efficiently, this capability can be much easier to implement than building a
binary counter (recall that a binary counter is a specialized adder but still
has a long carry-chain or larger and larger gates to do lookahead).
Binary counters with a large number of bits can be quite expensive in terms of
the logic they require. On the other hand, LFSRs with maximal sequences
can be made with input functions that are low fan-in (depend on only a few of
the register's outputs) and do not have a carry-chain. This makes LFSRs
very attractive when we need to count to large values but don't care about what
the patterns are (that is, they don't have to be consecutive binary
numbers). Variations of LFSRs are often used as random number generators
as well - consecutive output patterns can be made to look quite different and
are uniformally distributed over the
For example, a 4-bit LFSR with maximal length sequence will have the following
function: D1 = Q4 xor Q3. A larger 8-bit LFSR with D1 = Q8 xor Q7 xor Q6
xor Q1 will have a 255 pattern long maximal sequence.
Interestingly, a 32-bit LFSR can also have a maximal sequence (232-1 patterns
long) with a function of only 4 output variables, namely, D1 = Q32 xor Q31 xor
Q30 xor Q10.
Tasks- Part 2
1. Wire up your '377 octal D-FF to form a 4-bit shift register. Connect the four FF outputs to four of the LEDs. Connect the output of a 2:1 multiplexer to the first input with a switch connected to the mux's control input. The two mux inputs should be the value of another switch and the last output of the shift register (the fourth bit). Verify the operation of your shift register by setting the input to come from the switch. Go through a few clock cycles shifting in different values - basically, this is a four-bit version of the shift register you made at the end of the last lab assignment. Make sure to tie the enable input of the '377 to a value rather than leaving it floating.
2. Shift the pattern 1, 1, 0, 0 into your shift register. Flip the input mux switch so that the last output is now fed back into the input. Go through a few clock cycles. You should see your pattern shifting in a circular pattern through the register. How many different patterns are there in all before the output pattern on the LEDs repeats itself?
3. Invert the value of the last bit being fed back around before it goes into the mux. Repeat the previous task with this new configuration. How many different patterns do you see?
4. Remove the inverter and replace it with an XOR gate with the 4th and 3rd outputs as its inputs. Connect the output of this XOR gate to the input mux of the shift register. This is a 4-bit LFSR. Begin by shifting in zeros into your shift register (use the switch input to the mux). Now flip the mux to select the output of the XOR gate to be the input. Go through a few clock cycles. Does the pattern change? Now, shift in all ones (instead of zeros) to set up the shift register and then go through a few clock cycles. How many patterns do you go through before they begin to repeat? Is this a maximal sequence? Show your LFSR in operation to one of the TAs. Try different taps instead of 4th and 3rd, for example, 4th and 2nd. How many different patterns does this configuration generate? Demonstrate your LFSR to the TA to get checked off for Part 2.
Lab Demonstration/Turn-in Requirements:
This lab requires two seperate demonstrations for "checkoffs"
1. Turn in the completed timing diagram in Part 1. Demonstrate your 4-bit shift register from Part 1.
2. Demonstrate your LFSR from Part 2.