CSE370 Assignment 3

Distributed: 7 April 2000
Due: 14 April 2000

Reading:

1. Katz, Chapter 2 (pp. 40-85 and 92-102).
2. Katz, Chapter 3 (pp. 110-122).

Exercises:

1. Given f = (b' + d' + a)(c' + a')(b + d + a)(b + c + d' + a)

(a) Express f in canonical product-of-sums form (use M notation).
(b) Express f in canonical sum-of-products form (use m notation).
(c) Express f' in canonical product-of-sums form (use M notation).
(d) Express f' in canonical sum-of-products form (use m notation).
2. Determine the minimized realization of the following functions in sum-of-products form (use K-maps):

(a) f(A,B,C,D) = Sm(1,2,11,13,14,15) + d(0,3,6,10).
(b) f(A,B,C,D) = PM(2,5,6,8,9,10) * D(4,11,12).
(c) Katz exercise 2.20 (a).
3. A cable has four wires (A, B, C, D) placed in the order given. Each of the wires can carry a 1 or a 0. Write a logic function F(A, B, C, D) that is 1 if and only if a pair of adjacent wires is 0. Consider D to be adjacent to both C and A for symmetry. Express the function as a minterm expansion.
4. A combinational logic block has three inputs (A, B, C) and two outputs (Y1, Y0). The output variables represent a binary number where Y1 is the most significant bit. The binary number Y1 Y0 corresponds to the number of inputs that are 0. For example, if A=1, B=0, C=1, then only one value is 0 and the Y1=0, Y0=1. Express the two functions for Y1 and Y0 in minimized sum-of-products form.
5. Katz exercise 3.2 (d) (turn in a DesignWorks schematic).
6. Katz exercise 3.3 (d) (turn in a DesignWorks schematic).
7. Reverse engineer the circuit shown in the schematic below in order to minimize it into a more efficient implementation.


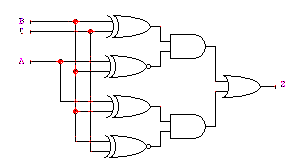
(a) Find the Boolean expression that describes the circuit.
(b) Construct the truth table for the function.
(c) Write the function in canonical sum-of-products form (little m notation).
(d) Simplify the function above using the axioms/theorems of Boolean algebra (show each step).
(e) Simplify the function again using a Karnaugh map. Give the Boolean equation that results from your simplification.
(f) Suppose your system specification suddenly changed (as frequently happens in the real world) and you now need a circuit that implements the complement of F. Show how you can use another instance of the K-map for F to find the minimized form of the complement F'. Give the minimized Boolean equation for F'.
(g) Draw the minimized F from part (e) and F' from part (f) in DesignWorks and verify their operation with binary switches and probes. Turn in your schematics.

Rationale:

• To practice and gain facility with two-level logic minimization.
• To practice basic combinational logic design.