Lab 7: Useful Components
Overview
Over the last six labs we've learned how to do most kinds of basic logic, but there are still more common elements that are useful for building more and more complex systems. This lab will help you get some experience with them now, and add them to your toolkit in advance of the final project.
Code for this lab
No code provided! Feel free to copy any needed files from previous labs or from lecture as a starting point.
Design Problem – CyberWar
In the last lab, we built a Tug of War game, and by now you've already crushed your roommate into submission. Now it's the hardware's turn. Your goal is to develop a computer opponent to play against, as well as a scorekeeper that can show exactly how badly it beats you…
Adder
In class, we developed a circuit for adding binary numbers. Implement a 10-bit Adder circuit in Quartus and simulate it to show that it is working. This will be used later on in the lab.
Since showing all input combinations for a 10-bit Adder (20 inputs!) is unreasonable, please simulate enough to cover the situations listed below. If you are unsure what any of these means, please ask!
- An addition with one input being 0.
- An addition whose result is 511.
- An addition whose result is 0 (other than 0 + 0).
- An example of unsigned overflow.
- An example of positive signed overflow (pos + pos = neg).
- An example of negative signed overflow (neg + neg = pos).
It can be helpful to display signals as decimal or hex values instead of the default binary. To do this, right-click on a multibit signal in ModelSim and select "Radix". Hex and Unsigned are particularly useful choices.
Counters
We will replace the "winner" system from Lab 6 with counters. Develop a 3-bit counter that satisfies the following behavior:
- Holds a 3-bit state (values 0-7).
- Starts at (and resets to) the value 0.
- When it receives a "win"/"count" input, it increments its current value by 1.
- It doesn't matter what happens when you count past 7 points.
Copy your Lab 6 files and alter them so that there is a counter for each player, each of which drive a 7-segment display with the current score for that player. Whenever someone wins, you increment the appropriate player's score and then restart the game (i.e., reset the playfield). Resetting the entire game will reset the playfield and score, while winning only resets the playfield.
Linear Feedback Shift Registers (LFSRs)
To build a cyber-player, we need to create a random number generator to simulate the button presses of your opponent. In hardware, a simple way to produce pseudo-random numbers is a linear feedback shift register (LFSR). It consists of a set of ℕ D flip-flops (DFF1 to DFFℕ), where the output of DFFi is the input of DFFi+1 (shifting bits linearly). The "randomness" comes from attaching some logical combination of the state bits (feedback) to the input of DFF1. By careful choice of the logical combination, we can get an FSM that is easy to implement but still goes through a fixed pattern of states that appears random.
In this lab, we will use the XNOR of two state bits as our input combination. Two examples are shown below:
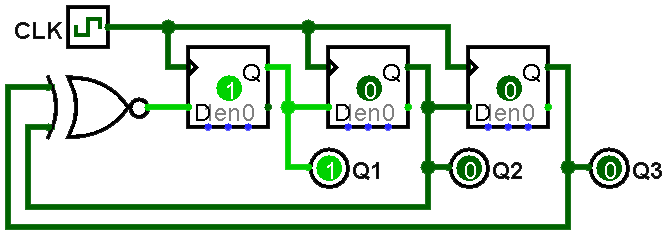
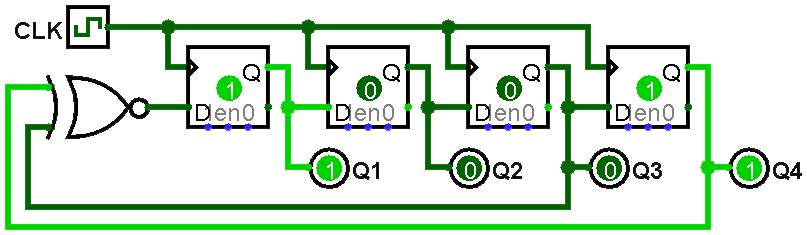
Draw state diagrams for the two LFSRs shown above. These will show every possible state for the machine (8 for the 3-bit, 16 for the 4-bit), with transition arrows showing the next state they will enter.
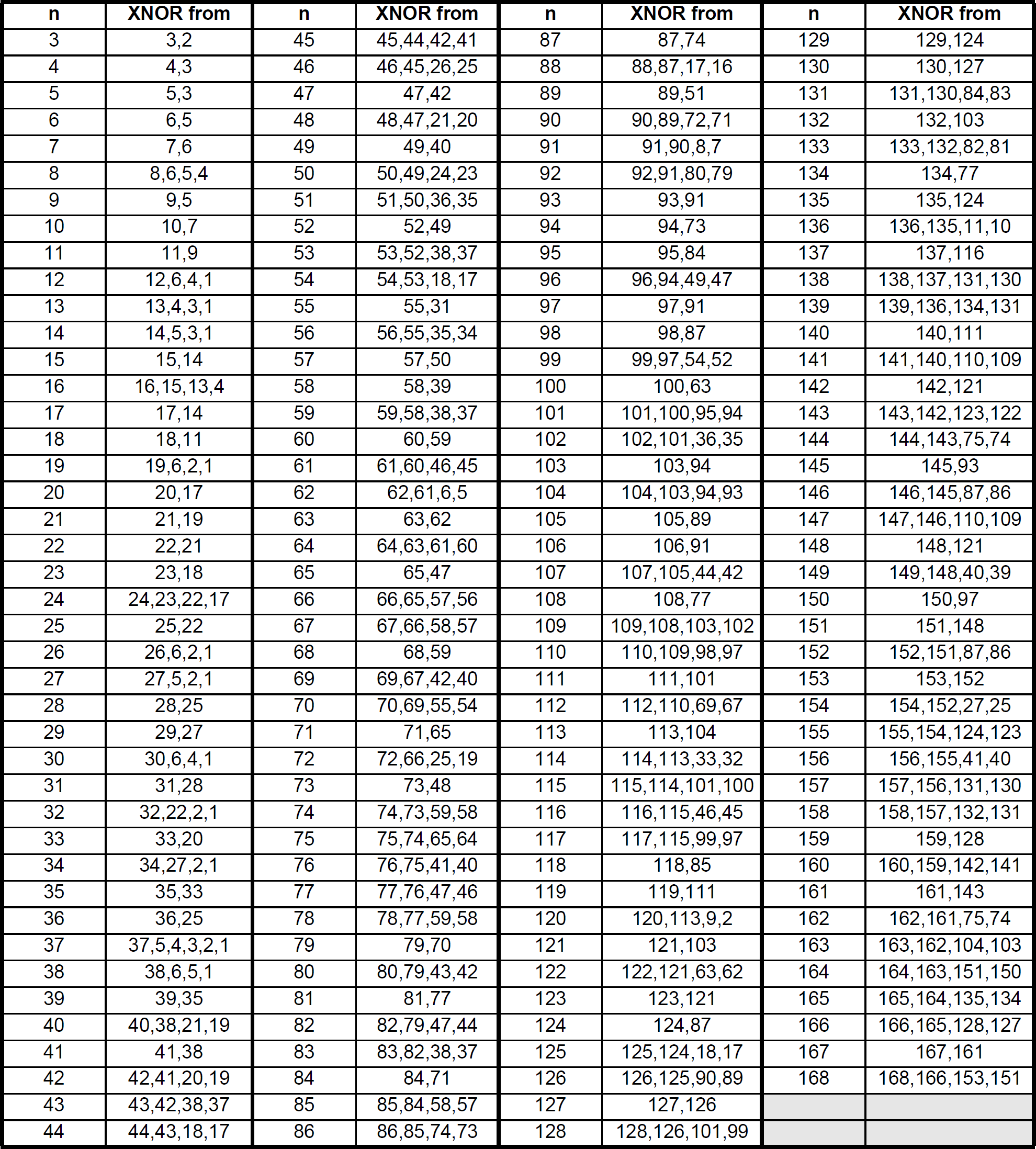
Next, create a 9-bit LFSR in Quartus and simulate it. You can find the list of bits to XNOR together by clicking the preview image below. "n" is the number of bits in your shift register and "XNOR from" indicates the state bits (numbered starting from 1) to pass as inputs to your XNOR gate to generate the maximum-length LFSR state sequence. How long is the cycle of states for this LFSR? Make sure your simulation proves this.
Cyber Player
Now let's implement a tunable cyber player!
Slow down the system so you stand a chance by running the game off of divided_clocks[15] (about 768 Hz). If later this still feels too fast, feel free to use a different divided_clock output.
Generate the computer's random button presses using the following procedure:
- Read an unsigned binary value from SW8-SW0 (a value from 0 to 511).
- Using the 10-bit adder you designed earlier, add the switch value to the LFSR output (another 9-bit unsigned value from 0 to 511).
- If and only if the sum is ≥ 512, the cyber player presses its button. Think carefully about how to determine if the result is ≥ 512 – there is a trivial implementation that will make your life easier!
The switch settings will bias how frequently the cyber player presses its button, making it tunable. Play with the switches to adjust the cyber player's mashing/pulling speed, to see how fast you can go!
Lab Requirements
Lab Report
Due before Wednesday section, submitted as a PDF on .
- State diagrams derived from the 3-bit and 4-bit LFSRs.
- Simulation of your working 10-bit adder that covers the 6 situations described.
- Simulation of your working 3-bit counter.
- Simulation of your working 9-bit LFSR with the state cycle length indicated.
- A screenshot of the "Resource Utilization by Entity" page, showing your design's computed size.
- How many hours (estimated) it took to complete this lab in total, including reading, planning, designing, coding, debugging, and testing.
- Separately, upload the SystemVerilog code (including test benches) for each module developed.
Lab Demo
Due by the end of the day on Friday, but typically during your assigned demo slot or a scheduled support hour.
- Demonstrate the simulation of your 10-bit Adder, 3-bit counter, 9-bit LFSR, and overall CyberWar design.
- Demonstrate your CyberWar system working on the DE1 board.
- Be prepared to answer questions on both the theoretical and practical parts of the lab.
Grading
Working Design
100 points for correctness, style, and testing.