Lab 7: Useful Components

Counters

  More reading for the curious: https://en.wikipedia.org/wiki/Counter_(digital)

We will replace the "winner" system from Lab 6 with counters. Develop a 3-bit counter that satisfies the following behavior:

• Holds a 3-bit state (values 0-7).
• Starts at (and resets to) the value 0.
• When it receives a "win"/"count" input, it increments its current value by 1.
• It doesn't matter what happens when you count past 7 points.

Copy your Lab 6 files and alter them so that there is a counter for each player, each of which drive a 7-segment display with the current score for that player. Whenever someone wins, you increment the appropriate player's score and then restart the game (i.e., reset the playfield). Resetting the entire game will reset the playfield and score, while winning only resets the playfield.

Linear Feedback Shift Registers (LFSRs)

  More reading for the curious: https://en.wikipedia.org/wiki/Linear-feedback_shift_register

To build a cyber-player, we need to create a random number generator to simulate the button presses of your opponent. In hardware, a simple way to produce pseudo-random numbers is a linear feedback shift register (LFSR). It consists of a set of ℕ D flip-flops (DFF₁ to DFF_ℕ), where the output of DFF_i is the input of DFF_i+1 (shifting bits linearly). The "randomness" comes from attaching some logical combination of the state bits (feedback) to the input of DFF₁. By careful choice of the logical combination, we can get an FSM that is easy to implement but still goes through a fixed pattern of states that appears random.

In this lab, we will use the XNOR of two state bits as our input combination. An example is shown below:

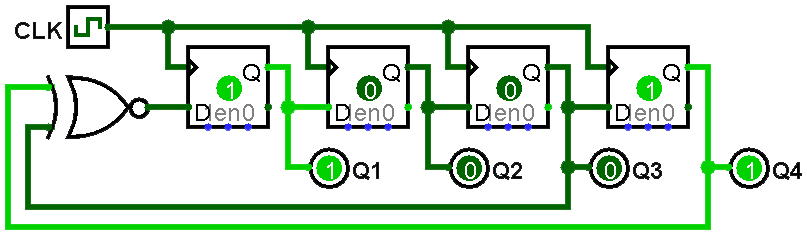
Draw the state diagram for the LFSR shown above. This should show every possible state for the machine (16 total), with transition arrows showing the next state they will enter (* is used to indicate an "always" transition).

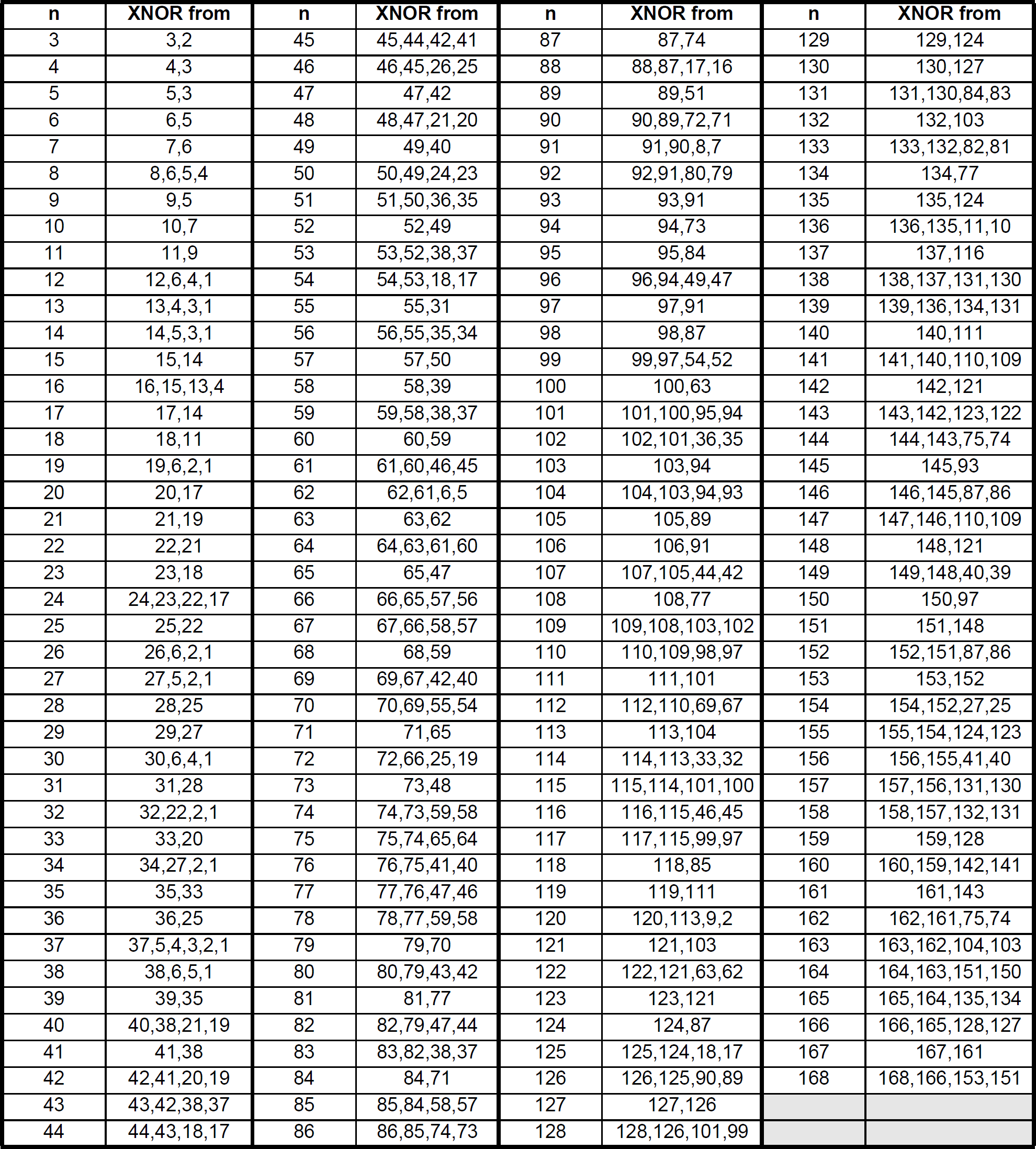
Next, create a 9-bit LFSR in Quartus and simulate it. You can find the list of bits to XNOR together by clicking the preview image below. "n" is the number of bits in your shift register and "XNOR from" indicates the state bits (numbered starting from 1) to pass as inputs to your XNOR gate to generate the maximum-length LFSR state sequence. How long is the cycle of states for this LFSR (i.e., how many cycles until a state reappears)? Make sure your simulation proves this in whatever way you feel is most appropriate (be creative!). Some example options:

• Split the waveform into multiple screenshots to make things more readable.
• Create an extra signal that only goes high when you're in a particular state.
• Look in the SystemVerilog Tutorial for how to use printing statements like $display.

Adders

In class, we developed a circuit for adding binary numbers. Implement either (1) a 9-bit adder with carry out or (2) a 10-bit adder and simulate it to show that it is working.

Since showing all input combinations for an adder of this size is unreasonable, please simulate enough to cover the situations listed below. If you are unsure what any of these mean, please ask!

1. An addition with one input being 0.
2. An addition whose result is 511.
3. An addition whose result is 0 (other than 0 + 0).
4. An example of unsigned overflow.
5. An example of positive signed overflow (pos + pos = neg).
6. An example of negative signed overflow (neg + neg = pos).

Cyber Player

Now let's implement a tunable cyber player!

Slow down the system so you stand a chance by running the game off of divided_clocks[15] (about 768 Hz). If later this still feels too fast or too slow, feel free to use a nearby divided_clock output.

Generate the computer's random button presses using the following procedure:

1. Read an unsigned binary value from SW8-SW0 (a value from 0 to 511).
2. Using the adder you designed earlier, add the switch value to the LFSR output (another 9-bit unsigned value from 0 to 511).
3. If and only if the sum is ≥ 512, the cyber player presses its button. Think carefully about how to determine if the result is ≥ 512 – there is a trivial implementation that will make your life easier!

The switch settings will bias how frequently the cyber player presses its button, making it tunable. Play with the switches to adjust the cyber player's mashing/pulling speed, to see how fast you can go!

Create a block diagram for your CyberWar system, either from scratch or by modifying your Lab 6 block diagram.

Simulate your overall system to show proper interconnections between modules.

Lab Report

Due before Wednesday section, submitted as a PDF on Gradescope.

• The top-level block diagram, showing the major modules and how they are interconnected.
  • Top-level ports should be shown as external inputs and output.
  • All instantiated modules should be shown as individual blocks with at least their module name labeled.
  • The name and directionality should be clear for all port connections.
  • Don't forget an accompanying explanation to help the reader.
• Simulation of your working 3-bit counter.
• State diagram of the 4-bit LFSR.
• Simulation of your working 9-bit LFSR with the state cycle length indicated.
• Simulation of your working 9- or 10-bit adder that covers the 6 situations described.
• Simulation of the top-level module.
• A screenshot of the "Resource Utilization by Entity" page, showing your design's computed size.
• How many hours (estimated) it took to complete this lab in total, including reading, planning, designing, coding, debugging, and testing.
• Separately, upload the SystemVerilog code (including test benches) for each module developed.

Lab Demo

Due by the end of the day on Friday, but typically during your assigned demo slot or a scheduled support hour.

• Explain your top-level block diagram.
• Demonstrate the simulation of your overall CyberWar design.
• Demonstrate your CyberWar system working on the DE1 board.
• Be prepared to answer questions on both the theoretical and practical parts of the lab.

Rubric