CSE 344 - Homework 6 Sample Solution

Problem 1:

Problem 2:

1. The relational schema is listed below. Key constraints, as usual, are specified by underlining. For foreign key constraints, we have used the convention that a field named B.key in table A is a foreign key referencing B. We have not included the "create table" statements; they can be easily obtained from the relational schema.

   InsuranceCo(name, phone)
   
   Vehicle(licencePlate, year, InsuranceCo.name, maxLiability, maxLossDamage,
           Person.ssn)
   
   Car(Vehicle.licencePlate, make)
   
   Truck(Vehicle.licencePlate, capacity, ProfessionalDriver.Driver.licenceNo)
   
   Person(ssn, name)
   
   Driver(licenceNo, Person.ssn), unique constraint on licenseNo
   
   ProfessionalDriver(Driver.licenceNo, medicalHistory)
   
   NonProfessionalDriver(Driver.licenceNo)
   
   Drives(Car.Vehicle.licencePlate, NonProfessionalDriver.Driver.licenceNo)
   

2. The "insures" relationship is many-one and this allows it to be included in the Vehicle relation. If a vehicle entity does not have insurance, these attributes will be NULL for it.
3. Drives is many-many and Operates is many-one. Drives requires an additional relation, while operates can be inlined into the Truck relation.

Problem 3:

1. There is a unique key (C,D,E).
   Both dependencies violate BCNF.
   Fixing D → B gives us (ACDE), (DB).
   Fixing CE → A gives us (CDE), (CEA), (DB) which is the final decomposition.
   
   
2. The keys for the relation are (A,C,D), (B,C,D) and (C,D,E).
   All given dependencies violate BCNF.
   Fixing BC → A gives us (BCDE), (BCA). The dependency A → E is also gone, so this is not a dependency-preserving decomposition.
   Fixing DE → B gives us (CDE), (DEB), (BCA) which is the final decomposition.
   
   An alternative approach: fixing A → E gives us (AE), (ABCD). The dependency DE → B is also gone.
   Fixing BC → A gives (ABC), (BCD), (AE) which is the final decomposition.
   
   Another alternative approach: fixing DE → B gives us (BDE), (ACDE). The dependency BC → A is also gone.
   Fixing A → E gives (BDE), (AE), (ACD) which is the final decomposition.
   

Problem 4:

1. Only trivial dependencies can exist. {} is one such set.
2. A->B, B->C, C->D, D->A
3. A->B, B->A, C->{ABD} and D->{ABC}

Problem 5:

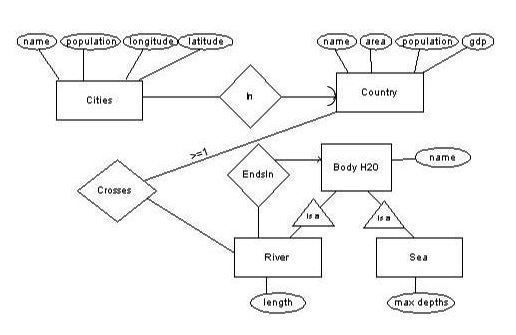
2. We assume that, as suggested in the instructions, you have loaded the data into a table called "hw1_data". The queries to help determine which functional dependencies exist are listed below.
   

   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name=H2.name and H1.discount !=H2.discount;
   --Returns a count of 36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name=H2.name and H1.month !=H2.month;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name=H2.name and H1.price !=H2.price;
   --0-->YES, is FD
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name!=H2.name and H1.discount =H2.discount; 
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.discount =H2.discount and H1.month !=H2.month; 
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.discount=H2.discount and H1.price !=H2.price;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name!=H2.name and H1.month =H2.month; 
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.discount!=H2.discount and H1.month =H2.month;
   --0-->YES, is FD
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.month =H2.month and H1.price !=H2.price;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name!=H2.name and H1.price =H2.price;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.discount!=H2.discount and H1.price =H2.price;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.month!=H2.month and H1.price =H2.price;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.month=H2.month and H1.price =H2.price and H1.name!=H2.name;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.month!=H2.month and H1.discount=H2.discount and H1.name=H2.name;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.month!=H2.month and H1.discount=H2.discount and H1.price=H2.price;
   --36
   
   select count(DISTINCT H1.name)
   from hw1_data H1, hw1_data H2
   where H1.name!=H2.name and H1.discount=H2.discount and H1.price=H2.price;
   --36
   

   The dependencies are name->price and month->discount.
   
   
3. The BCNF decomposition is:
   R1 (name, price)
   R2 (name, month)
   R3 (month, discount)
   
   The "create table" statements are listed below:
   

   create table NamePrice ( -- R1
     name varchar(20) primary key, 
     price real
   );
   
   create table MonthDiscount ( -- R3
     month varchar(20) primary key, 
     discount varchar(10)
   );
   
   create table NameMonth ( -- R2 
     name varchar(20) references NamePrice(name), 
     month varchar(20) references MonthDiscount(month)
   );
   

4. Here is the code to populate the tables:

   insert into NamePrice
     select distinct name, cast(price as real) as the_price
     from hw1_data;
   
   insert into MonthDiscount
     select distinct month, discount
     from hw1_data;
   
   insert into NameMonth
     select name, month
     from hw1_data;
   

   Note that (name,month) is the key for hw1_data, so the "distinct" modifier is not needed for NameMonth.