Understanding Quantitative Data

name: inverse
layout: true
class: center, middle, inverse
---
# Analyzing Quantitative Data

Jennifer Mankoff

CSE 340 Winter 2020
---
layout:false

[//]: # (Outline Slide)
.title[Today's goals]
.body[
- Discuss how we determine causality
- Practice onboarding participants
- Practice data analysis
]
---
# How do we determine *causality*?

Implies *dependence* between variables

Assumes you have measured the right variables!

---
# Dependence/independence

Events that are independent
- Flipping heads and then tails
- Day of week and whether a patient had a heart attack (probably?)

Events that are dependent
- Vice presidential candidate and presidential nominee
- Diagnostic test being positive and whether patient has a disease

???
What if we collect this kind of data, what might be true about it?

---
# What might we expect to see is true of dependent variables?

- When one changes, the other changes at the same rate
- When one changes, the other changes at a faster rate
- When one changes, the other does the opposite

???
Called a correlation
We can see it in a scatter plot
Go look at data and make one

---
# This is called *Correlation*

We can see it in a *scatterplot*

![:img Example of correlations for heigh vs age (positively correlated) and
height vs birth month (uncorrelated),60%](img/studies2/correlation.png)

---
# Correlation demo

[OpenSecrets.org data set on internet privacy resolution](https://www.opensecrets.org/featured-datasets/5)

Open it yourself:
[tinyurl.com/cse340-ipdata](https://tinyurl.com/cse340-ipdata)

--
![:img Correlation of company giving,60%](img/studies2/correlation-demo.png)

---
# Correlation != Causation

![:img Correlation of number of people who drowned per year and films
nicolas cage appeared in, 80%](img/studies2/cagelation.png)

---
# Correlation != Causation

![:img Two people talking. Says one: I used to think correlation
implied causation. Says the other: Then I took a statistics
course. Now I don't. Says the other: Sounds like the class
helped. Says the first: Well maybe, 50%](img/studies2/correlation-cartoon.png)

---
# Grouping for analysis

Pivot Tablest demo
[tinyurl.com/cse340-ipdata](https://tinyurl.com/cse340-ipdata)

--
![:img Giving vs party for diff votes, 30%](img/studies2/pivot1.png)

---
# Grouping and charting helps you check your assumptions

speed: 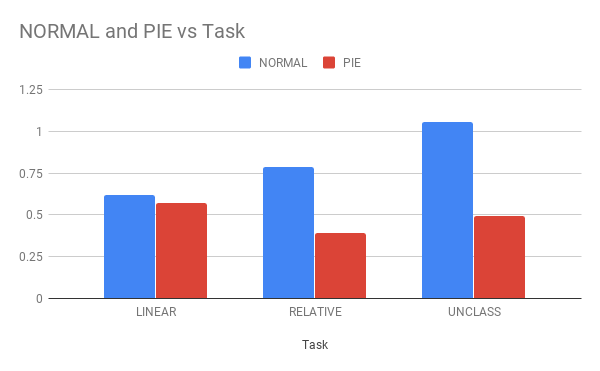![:img Image of bar chart comparing tasks to menu type showing that
normal menus get progressively slower as items become nonlinear while
pie menus are about the same, 40%](img/studies2/chart.png)

--
[tinyurl.com/cse340-20w-data](https://tinyurl.com/cse340-20w-data)

Not that different in my sample set (just me doing it 3 times). We
hope to see better results in your data, and even better if we merge
all your data!

---
# Comparing two groups to see if they are different
Bar charts  are not enough to assess difference though. Need to see the *distribution*

---
# Histogram shows you a *distribution*

Pivot Tablest demo
[tinyurl.com/cse340-ipdata](https://tinyurl.com/cse340-ipdata)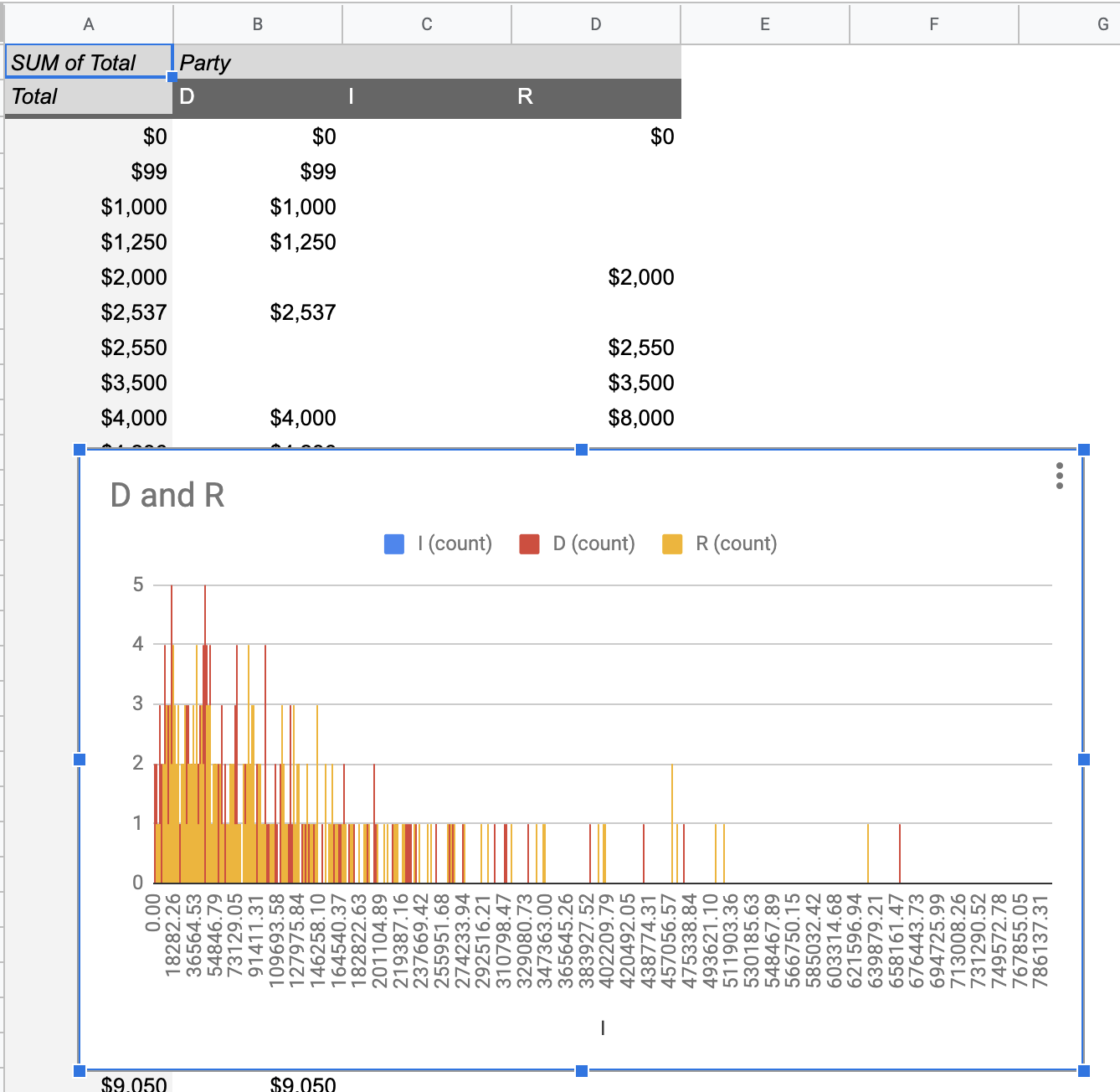

--
![:img Histogram of amount vs party, 40%](img/studies2/pivot2.png)

---
# But having the right chart matters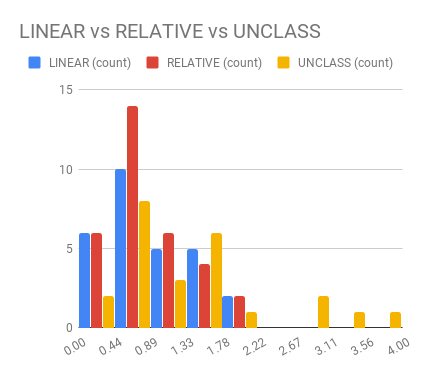

![:img Histogram of data about speed of pie menu selection and linear
menu selection for each task type, 40%](img/studies/histogram.png)

---
# Normal Vs Pie

|Normal | Pie|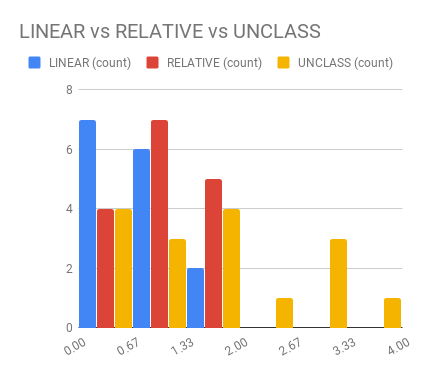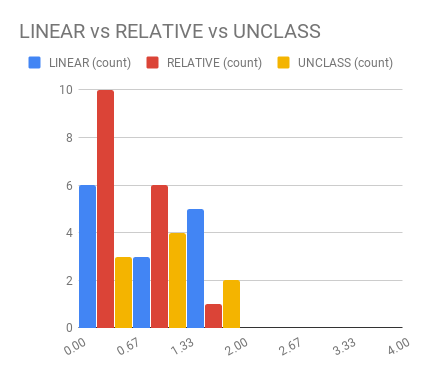
|--|--|
|![:img Histogram of data about speed of pie menu selection and linear menu selection for each task type,100%](img/studies/normal-only.png)|![:img Histogram of data about speed of pie menu selection and linear menu selection for each task type, 100%](img/studies/pie-only.png)|

The cause of the difference only shows here.

---

# What do we learn from a histogram?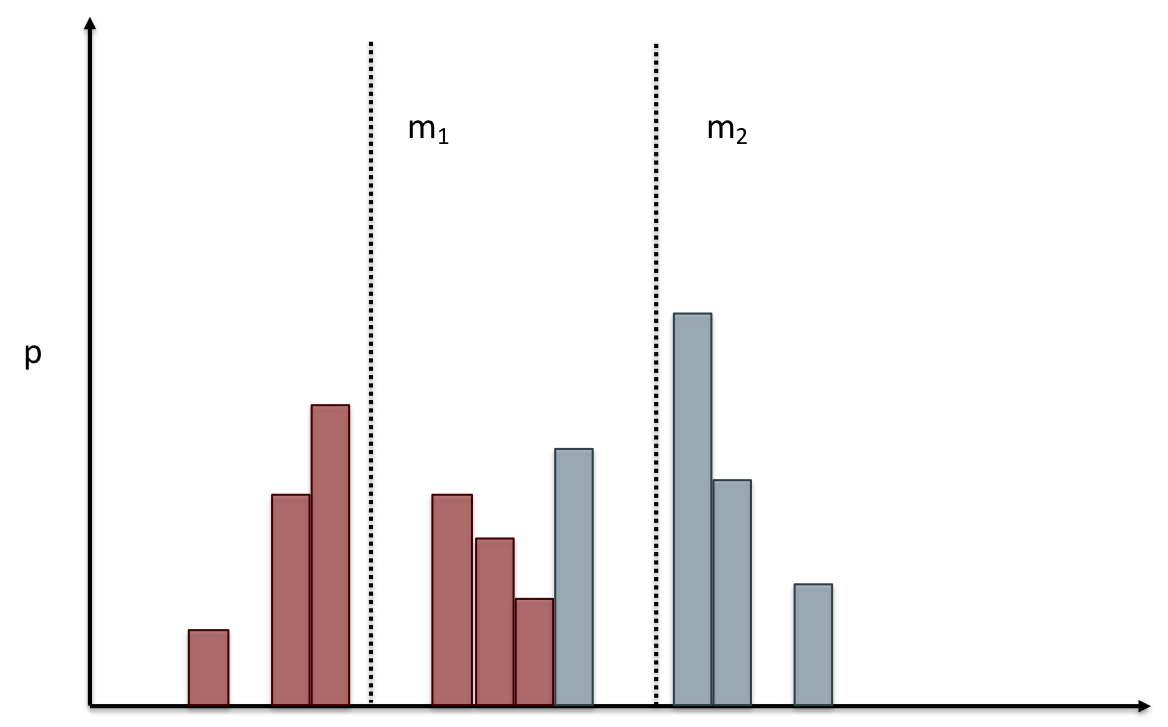

![:img two distributions, 50%](img/studies/samples1.png)

???
- shows a distribution
- helps us tell if things are INDEPENDENT

---
#  Histograms

What do we learn from a histogram?
- shows a distribution
- helps us tell if things are INDEPENDENT

---
# Comparing two groups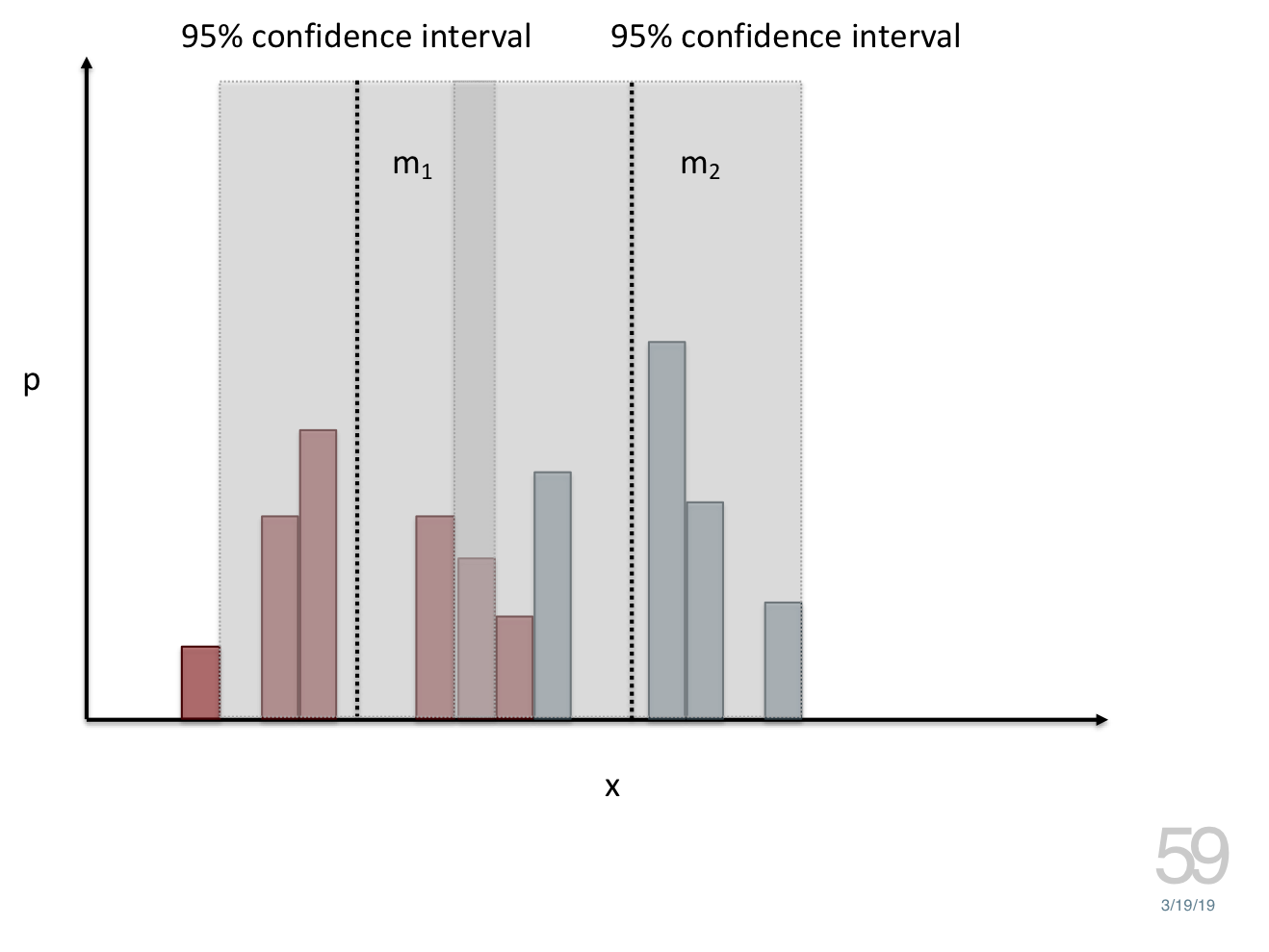

![:img two distributions showing overlapping 95% confidence intervals,
50%](img/studies/samples2.png)

---
# Comparing two groups

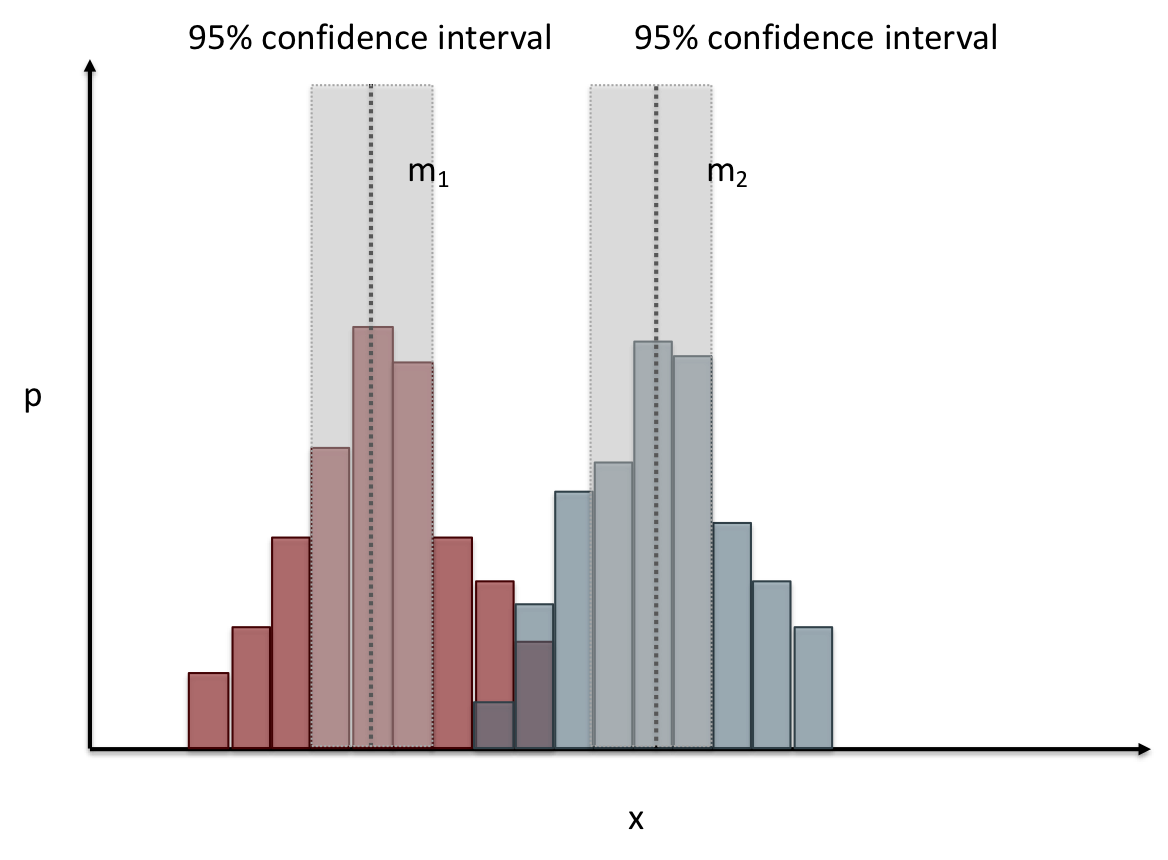![:img two distributions with less overlapping intervals (because more
data is present), 50%](img/studies/samples3.png)

---
# Comparing two groups

![:img two distributions with more data but overlapping histograms
thus hard to differentiate, 50%](img/studies/samples4.png)

---
# Comparing two groups

![:img two distributions with less overlapping intervals (because more
data is present), 50%](img/studies/samples5.png)

---
# Comparing two groups

![:img two distributions not overlapping at all, 50%](img/studies/samples6.png)

---
# Comparing two groups

![:img same two distributions with difference between means marked as
effect size, 50%](img/studies/samples7.png)

---
# Common Statistical Test for comparison: t-test

Tests for difference between two samples

Best used to determine what is ‘worthy of a second look’

Limited in its applicability to normal, independent data

Does not help to document effect size [the actual difference between groups], just effect likelihood

---
.left-column[
## Problems with t-tests

The more implausible the hypothesis, the greater chance that it is a
‘false alarm’
]
.right-column[
![:img A picture of the likelihood of a positive t-test as influenced by
priors (the expected likelihood of an outcome), 80%](img/studies/priors.png)

]
???
Top row: Prior (what's known to be true before the experiment)
bottom row: Calculated p-value

Notice the middle column, where something that is a toss-up has higher
plausability than we would expect. This is a "Type 1 error"

Alternatively, a small sample may cause a Type II error (failure to
detect a true difference) due to random sampling bias

---
.left-column[
## Problems with t-tests
]
.right-column[
- Doesn’t take prior knowledge into account
- Susceptible to ‘data dredging’
 - The more tests you conduct the more likely you will find a result
   even if one is not there
 - Adjustments mid experiment
- Gives a yes or no answer: Either the null hypothesis is rejected (the result would be unlikely in a world where the null hypothesis was true) or it cannot be rejected
- Based on assumed ‘average’ sample
]
---
# Which problems might affect our study?

???
Too many comparisons
--

18 separate comparisons (3x3 conditions, 2 measures)

ANOVA (**An**alysis **O**f **Va**riance): Fancy t-test that accounts for the whole group effect before
doing pairwise comparisons

???
- Doesn’t take prior knowledge into account
- Susceptible to ‘data dredging’
 - The more tests you conduct the more likely you will find a result
   even if one is not there
 - Adjustments mid experiment
- Gives a yes or no answer: Either the null hypothesis is rejected (the result would be unlikely in a world where the null hypothesis was true) or it cannot be rejected
- Based on assumed ‘average’ sample

---
# Demo of t-tests in our spreadsheet

[tinyurl.com/cse340-20w-data](https://tinyurl.com/cse340-20w-data)

---
.left-column[
## Document what all of this in your [report](/courses/cse340/20wi/assignments/menu-report)
]
.right-column[

- Describe your hypothesis
- Illustrate with graphs
- Optional: use Table of results found in `Speed Analysis` and `Error Analysis` to describe Statistical Significance:

`Pie menus were twice as fast as normal menus (M=.48s vs M=.83s), F(1,43)=295.891, p<.05. Unclassified menu items were harder to find than linear and relative ones (M=.84s, .59s, and .59s respectively), F(2,43)=93.778, p<0.5. We also found an interaction effect between menu and task (as illustrated in the chart above), F(5, 43) = 51.945, p<.001.`

]

---
# Drawing Conclusions

.left-column[
<div class="mermaid" style="font-size:.5em">
graph TD
S(.) --> Hypothesis(Hypothesis:<br>Decreased seek <br>time and errors)
Hypothesis -- "Study Design" --> Method(3 menus x <br> 3 task conditions )
Method -- "Run Study" --> Data(Data)
Data -- "Clean and Prep" --> Analysis(Analysis)
Analysis --> Conclusions(Conclusions)

classDef finish outline-style:double,fill:#d1e0e0,stroke:#333,stroke-width:2px,font-size:.7em,height:2.5em;
classDef normal fill:#e6f3ff,stroke:#333,stroke-width:2px,font-size:.7em,height:2.5em;
classDef normalbig fill:#e6f3ff,stroke:#333,stroke-width:2px,font-size:.7em,height:4em;
classDef start fill:#d1e0e0,stroke:#333,stroke-width:4px,font-size:.7em,height:5em;
classDef startsmall fill:#d1e0e0,stroke:#333,stroke-width:4px,font-size:.7em,height:2.5em;
classDef invisible fill:#FFFFFF,stroke:#FFFFFF,color:#FFFFFF

linkStyle 0 stroke-width:3px;
linkStyle 1 stroke-width:3px;
linkStyle 2 stroke-width:3px;
linkStyle 3 stroke-width:3px;
linkStyle 4 stroke-width:3px;

class S invisible
class Hypothesis start
class Conclusions startsmall
class Method normalbig
class Data,Analysis normal
</div>

]

.right-column[
- Describe your hypothesis
- Illustrate with graphs
- Optional: Statistical Significance

Draw Conclusions
- Were errors less?
- Was time faster?

`Describe your conclusions. Do you think we should use pie menus more? What can we conclude from your data?`
]

---
# Limitations of Laboratory Studies

???
Simulate real world environments
- Location and equipment may be unfamiliar to participant [Coyne & Nielsen 2001]
- Observation may effect performance - “Hawthorne Effect” [Mayo 1933]
- Participant may become fatigued and not take necessary rest - “Demand Effect” [Orne 1962]
- Tasks frequently artificial and repetitive, which may bore participants and negatively effect performance
Studying real world use removes these limitations

Simulate real world environments
- Location and equipment may be unfamiliar to participant [Coyne & Nielsen 2001]
- Observation may effect performance - “Hawthorne Effect” [Mayo 1933]
- Participant may become fatigued and not take necessary rest - “Demand Effect” [Orne 1962]
- Tasks frequently artificial and repetitive, which may bore participants and negatively effect performance
Studying real world use removes these limitations