Contents:
This assignment lays the groundwork for an application you'll build in Homeworks 7 and 8 called Campus Paths. Using your graph as the underlying data structure, Campus Paths generates directions between buildings on campus to help students and visitors find their way around.
This assignment has two main parts. In the first part, you will make your graph class(es) generic. In the second part, you will implement a more advanced pathfinding algorithm for graphs known as Dijkstra's algorithm. These parts are not directly related to each other, but both are necessary for Homework 7.
In Campus Paths, your mission is to find the shortest walking route between points on the UW campus. A graph is an excellent representation of a map, and luckily you have already specified and implemented a graph. Unfortunately, your graph only stores Strings, whereas Campus Paths needs to store non-String data types in the nodes and edges, such as coordinate pairs and physical distances. More generally, your graph would be much more widely useful if only the client could choose the data types to be stored in nodes and edges. Herein lies the power of generics!
Your task is to convert your graph ADT to a generic class. Rather than always storing the data in nodes and edge labels as Strings, it should have two type parameters representing the data types to be stored in nodes and edges. Directly modify your existing classes under hw4 — there is no need to copy or duplicate code.
When you are done, your previously-written HW4 and HW5 tests and test driver and MarvelPaths will no longer compile. Modify these classes to construct and use graph objects parameterized with Strings. All code must compile and all tests must pass when you submit your homework. In particular, your test drivers for both Homework 4 and 5 must work correctly so we can test your code. Depending on your changes, some of your implementation tests may no longer be valid. Try to adapt your implementation tests to your new implementation, or discard them and write new ones: they should help you build confidence in your implementation. But, don't overdo it: as with any testing, stop when you feel that the additional effort is not being repaid in terms of increased confidence in your implementation. Learning when to stop working on a given task is an important skill.
Double-check that you have configured Eclipse to issue errors for improper use of generic types.
Very important warning! Eclipse's built-in compiler sometimes handles generics differently from javac, the standard command-line compiler. This means code that compiles in Eclipse may not compile when we run our grading scripts, leaving us unable to test your code and significantly impacting your grade. You must periodically make sure your code compiles (builds) with javac by running ant build from the hw6 directory (which will also build hw4 and hw5 automatically). You can do this in one of two ways:
If Ant reports that the build succeeded, all is well: your code compiles with javac.
Hint: after encountering build errors in Ant, you may find that classes which previously compiled are now reporting "[some class] cannot be resolved" errors in Eclipse. You can fix these errors by doing a clean build: go to Project >> Properties >> Clean..., select your cse331 project, and hit OK.
In a weighted graph, the label on each edge is a length, cost, or weight representing the cost of traversing that edge. Depending on the application, the cost may be measured in time, money, physical distance, etc. The total cost of a path is the sum of the costs of all edges in that path, and the minimum-cost path between two nodes is the path with the lowest total cost between those nodes.
In Homework 7, you will build a edge-weighted graph where nodes represent locations on campus and edges represent straight-line walking segments connecting the two locations. The cost of an edge is the physical length of that straight-line segment. Finding the shortest walking route between two locations is a matter of finding the minimum-cost path between them.
You will implement Dijkstra's algorithm, which finds a minimum-cost path between two given nodes. Below is a pseudocode algorithm that you may use in your implementation. You are free to modify it as long as you are essentially still implementing Dijkstra's algorithm. Your implementation of the algorithm may assume a graph with Double edge weights.
The algorithm uses a data structure known as a priority queue. A priority queue stores elements that can be compared to one another, such as numbers. A priority queue has two main operations:
For example, if you inserted the integers 1,8,5,0 into a priority queue in that order, they would be removed in the order 0,1,5,8. It is permitted to interleave adding and removing. The standard Java libraries include an implementation of a PriorityQueue.
start = starting node
dest = destination node
active = priority queue. Each element is a path from start to a given node.
A path's "priority" in the queue is the total cost of that path.
Nodes for which no path is known yet are not in the queue.
finished = set of nodes for which we know the minimum-cost path from start.
// Initially we only know of the path from start to itself, which has a cost
// of zero because it contains no edges.
Add a path from start to itself to active
while active is non-empty:
// minPath is the lowest-cost path in active and is the minimum-cost
// path for some node
minPath = active.removeMin()
minDest = destination node in minPath
if minDest is dest:
return minPath
if minDest is in finished:
continue
for each edge e = ⟨minDest, child⟩:
// If we don't know the minimum-cost path from start to child,
// examine the path we've just found
if child is not in finished:
newPath = minPath + e
add newPath to active
add minDest to finished
If the loop terminates, then no path exists from start to dest.
The implementation should indicate this to the client.
You will write a modified version of your Marvel Paths application in which your application finds paths using Dijkstra's algorithm instead of BFS. Your algorithm should use, as the weight of the edge between two characters, the multiplicative inverse of the number of edges in the multigraph between them. For example, if Amazing Amoeba and Zany Zebra appeared in 5 comic books together, the weight of the edge between them would be 1/5. Thus, the more well-connected two characters are, the lower the weight and the more likely that a path is taken through them.
Place your new Marvel application in hw6/MarvelPaths2.java. In choosing how to organize your code, remember to avoid duplicating code as much as possible. In particular, reuse existing code where possible, and keep in mind that you will be reusing Dijkstra's algorithm for a different application (unrelated to Marvel comic books) in Homework 7.
As before, your program must be able to construct the graph and find a path in less than 30 seconds on attu using the full Marvel dataset. ScriptFileTests is set to put a 3000 ms (30 second) timeout for each test.
Also as before, you are welcome to write a main() method for your application, but you are not required to do so.
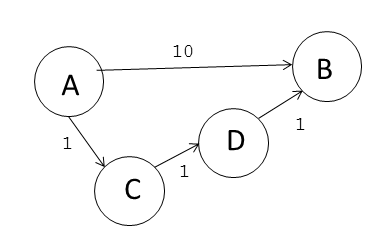
This assignment does not reuse your breadth-first search algorithm. A breadth-first search between two nodes finds the path with the fewest number of edges. In a weighted graph, it does not always find the minimum-cost path. In the example below, a breadth-first search from A to B would find the path {⟨A,B⟩} with total cost 10. But the alternative path {⟨A,C⟩,⟨C,D⟩,⟨D,B⟩} has a total cost of 3, making it a lower-cost path even though it has more edges.

Breadth-first search gives the same results as Dijkstra's algorithm when all edge weights are 1.
The format for writing tests follows the usual specification/implementation structure. You should write the majority of your tests as specification tests according to the test script file format defined below, specifying the test commands, expected output, and graph data in *.test, *.expected, and *.tsv files under, respectively. The *.tsv files should be structured in the same format as marvel.tsv. As usual, you will also write a class HW6TestDriver to run your specification tests. We provide a starter file for the test driver which you are free to modify or replace.
If your solution has additional implementation-specific behavior to test, write these tests in a regular JUnit test class or classes and add the class name(s) to ImplementationTests.java.
The specification tests do not directly test the property that your graph is generic. However, the Homework 4 and Homework 5 test scripts use String edge labels, while Homework 6 uses numeric values. Supporting all three test drivers implicitly tests the generic behavior of your graph.
Please answer the following questions in a file named reflection.txt in your answers/ directory.
Please answer the following questions in a file named collaboration.txt in your answers/ directory.
The standard collaboration policy applies to this assignment.
State whether or not you collaborated with other students. If you did collaborate with other students, state their names and a brief description of how you collaborated.
After you receive your corrected assignment back from your TA, you will need to resubmit a corrected version of the code. You will have until Tuesday, May 29 at 11pm to returnin your code. The returnin script will be enabled a week earlier, at 11pm Tuesday, May 22.
You will only receive credit if you pass all the tests, and you have a fixed number of trials without penalty. See the returnin331 documentation for details.
The test script file format for Homework 6 uses exactly the same commands and format as Homework 5, but with a few differences in arguments and output:
path from CHAR 1 to CHAR N: CHAR 1 to CHAR 2 with weight w1 CHAR 2 to CHAR 3 with weight w2 ... CHAR N-1 to CHAR N with weight wN-1 total cost: W
where W is the sum of w1, w2, ..., wN-1.
In other words, the only changes in output from HW5 are the way the edge labels are printed and the addition of a "total cost" line at the bottom. The output should remain the same as before when no path is found or the characters are not in the graph: in particular, do not print the "total cost" line in those cases. Also as before, underscores in node names are replaced by spaces for this command.
If there are two minimum-cost paths between CHAR 1 and CHAR N, it is undefined which one is printed.
String.format("Weight of %.3f", 1.759555555555);
In FindPaths, the total cost should be computed by summing the full values of the individual weights, not the rounded values.
Several sample test files demonstrating the changes in format are provided in hw6/test.
You should add and commit the following files to SVN:
Additionally, be sure to commit any updates you make to the following files:
Finally, remember to run ant validate to verify that you have submitted all files and that your code compiles and runs correctly when compiled with javac on attu (which sometimes behaves differently from the Eclipse compiler).
When printing edge weights, you should round to the closest value instead of truncating. Rounding is the default behavior provided by Java's format strings.
There was a mistake in the original version of exampleMarvelBasicSearch.expected pushed to your repositories. Please update your repository to receive the corrected version.
None yet!