CSE 326, Winter 2005: Homework 4

Due 2/4/2005

For all program or data structure design problems such as the those below you must provide pseudocode and an adequate explanation of the methods. It is often helpful to include small examples demonstrating the methods. Straight pseudocode with no additional documentation is not enough.  Your pseudocode can contain English if needed.  Each problem should be answered on a separate sheets of paper so they can be graded by different TAs.  Your name should be at the top of every page.

1. (a) (5 points) Present pseudocode for the recursive function
   Eval(tree: node pointer)
   which evaluates an expression tree containing the binary operators + and * and integers. Nodes are defined as follows:

record node: ( flag: integer, value: integer, left: node pointer, right: node pointer )
where
flag = 0 means the node represents an integer stored in the value field,
flag = 1 means the node represents multiplication,
flag = 2 means the node represents addition

(b) (5 points) Compilers often try to optimize the evaluation of expressions by finding repeated occurrences of a sub-expression, and making sure that the sub-expression is only calculated once. One way of doing this to convert an expression tree to an expression directed acyclic graph (DAG). For example, the expression 3*4 + 3*4 + 7*3*4 is represented by the follow tree, which represents the sub-expression 3*4 three time:

A smart compiler might convert the tree to the following DAG:

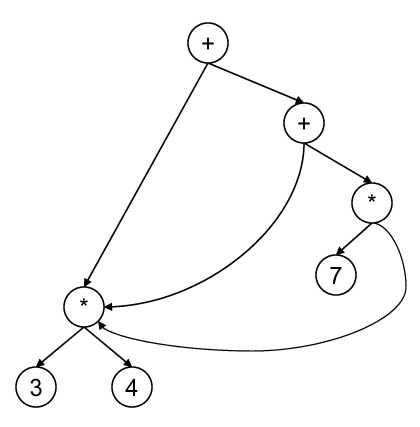
First, answer the following question: If you call your original Eval function on the top node of this or any other such expression DAG, will it always get the correct answer? Why or why not?

Next, modify your Eval function so that it does less work on an expression DAG by only calculating the value of each common sub-expression once. You may modify the definition of a node by adding a single Boolean (true or false valued) field.

2. (10 points) Write pseudocode for an iterative procedure that prints out a tree in row-by-row order. For example, given the following tree:

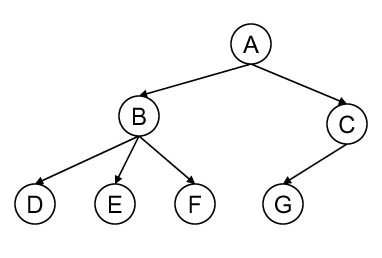
your function should print A B C D E F G. Assume the tree is represented using the first-child/next-sibling approach. Important hint: your program will make use of a FIFO (first-in, first-out) queue. You should decide on a way to represent the queue, and include this in your pseudocode. It is up to you whether you want to define the queue as an explicit data type using its own set of access functions, or whether you simply implement the queue as part of the overall printing procedure.

3. (a) (5 points) Consider the task of printing a range of values that are stored in a binary search tree. For example, for the following tree:

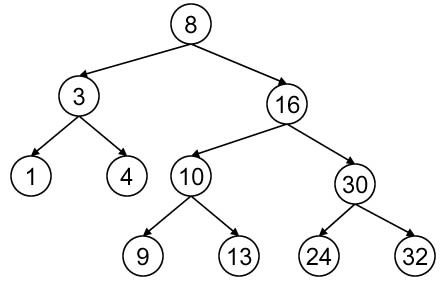
a call to PrintRange(root, 4, 24) would print 4 8 9 10 13 16 24. Present pseudocode for an efficient recursive implementation of
PrintRange(root: node pointer, low: integer, high: integer)
You may assume that the values low and high actually appear in the tree.

(b) (5 points) Analyze your algorithm, and prove that if the tree is complete (perfectly balanced) it runs in time
O(k + log n)
where n is the number of nodes in the tree, and k is the number of values printed out.