Friday, October 26, 2001
CSE 326 Autumn 2001
Quiz 2
1. (3 points) Define the binary search tree property.
2. (3 points) Define the AVL tree property.
3. (2 points) Pre-order and post-order tree traversal are best described as:
|
a) First-in first-out (FIFO) |
b) Depth-first search |
|
c) Breadth-first search |
d) Last-in first-out (LIFO) |
|
e) Garbage-in garbage-out (GIGO) |
|
4. (5 points) Indicate which type of tree traversal best solves each of the following (pre-order, post-order, level-order, or in-order):
a. ( Pre Post Level In ) Computing the depth of all nodes in a tree.
b. ( Pre Post Level In ) Computing the height of a node
c. ( Pre Post Level In ) Printing a directory listing, like:
DirectoryA
File1.txt
File2.txt
DirectoryA1
File3.txt
DirectoryB
File4.txt
d. ( Pre Post Level In ) Printing a graphical organization chart, like:
|
|
|
The Whole
Dang Company |
|
|
|
|
|
| |
|
|
|
| |
|
| |
|
| |
|
Finance |
|
Manufacturing |
|
Dept of
Obfuscation |
|
| |
|
|
|
| |
|
Accounting |
|
|
|
Confusion
Team |
e. ( Pre Post Level In ) Computing the size of a node (number of nodes at or below the given node).
5. (2 points) Suppose we wanted to keep track of duplicate items in a tree, i.e. those items which share a common key, by keeping a linked list of duplicates. Which of the following members in the TreeNode data structure would it make the most sense to replace with the linked list of duplicates?
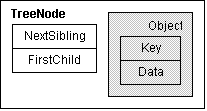
a. FirstChild
b. NextSibling
c. Object
d. Key
e. Data
f. None of the above. We would add a new member to hold the linked list of duplicates.
6. You are given the root of a binary tree and a pointer to one of the nodes in the tree, and you need to generate the path from the root to the given node. Assume that tree nodes contain no parent pointers.
- (2 points) Which technique is best-suited to finding the root-to-node path of a given node?
|
a) Pre order traversal |
b) Level order traversal |
|
c) Depth first search |
d) In order traversal |
|
e) Post order traversal |
|
- (3 points) Which expression best bounds your technique’s running time, as a function of node depth d?
|
a) Q(d) |
b) Q(log d) |
|
c) O(log d) |
d) Q(2d) |
|
e) O(d2) |
|
- (2 points) Which expression best bounds the running time as a function of N, where N is the number of nodes in the tree?
|
a) Q(N) |
b) Q(log N) |
|
c) O(log N) |
d) Q(2N) |
|
e) O(N2) |
|
7. Now assume that tree nodes contain parent pointers. You are given the root of a binary tree and a pointer to one of the nodes in the tree, and you need to generate the path from the root to the given node.
a. (5 points) Describe an algorithm for finding the root-to-node path of a given node which best exploits parent pointers.
b. (2 points) Which expression best bounds the running time of your algorithm, as a function of node depth d?
|
f) Q(d) |
g) Q(log d) |
|
h) O(log d) |
i) Q(2d) |
|
j) O(d2) |
|
8. Suppose a node has just been inserted into subtree X of the AVL tree below, and the heights of the subtrees after the insertion are as indicated.
a. (2 point) Which AVL operation should be used to fix up the tree?
b. (1 point) On which node will the AVL operation be applied? (Hint: apply the AVL operation to the node which is out of balance.)
c. (3 points) Show at each stage how the tree changes until the insert operation is complete.
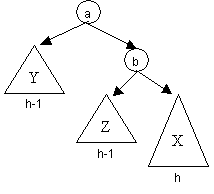
9. (2 points) In a splay tree, we base our decision of which splay operation to perform upon which of the following criteria?
a. Depth of the node being splayed.
b. Ancestry of the node being splayed.
c. Height of the node being splayed.
d. All of the above.
e. None of the above.
10. (3 points) Splay tree operations.
a. ( T F ) Splaying nodes in a binary search tree on find, insert and delete is guaranteed to maintain the tree’s binary search tree property.
b. ( T F ) No find, insert or delete operation in a splay tree can ever run in W(n) time.
c. ( T F ) Splaying tends to pull nodes along the access path closer to the root.
11. (Extra Credit - 5 points) Prove that the following assertion is false:
Splaying nodes in an AVL
tree on find, insert and delete is guaranteed to maintain the tree’s AVL tree
property.
You may base your proof on a counter-example, generated by performing a splay find operation on the following AVL tree.
a. (1 point) Which node is the splay find operation performed on?
b. (3 points) Show at each stage how the tree changes until the splay find operation is complete.
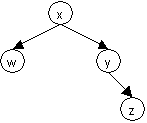
c. (1 point) Why is the final tree not an AVL tree?