


Next: About this document
`|=
|#1|#1
`@=
@#1@#1
Discrete Structures Anna Karlin, 426C Sieg
CSE 321, Spring 1998
Homework #5
Due at the beginning of class, Wednesday, May 13
Reading: Rosen, Sections 4.1 - 4.4
New Experimental Policy: You are strongly encouraged to work
in groups of 2 on this homework and turn in a single homework with both
names on it. Both members of the group will receive the same
score.
-
Consider the following variant of the stable pairing problem, which
we'll call the "general stable pairing problem" (this is the bisexual
version): We are given 2n people, each with a complete ranking of
the remaining 2n-1 people (no ties). A "pairing" of the 2n people
is a partition of the 2n people into n couples. A pairing is
"unstable" if there are two people (not a couple) that both prefer
each other to the people with whom they are coupled. A pairing is
"stable" if it it not unstable. Prove that there exist preference
lists for which there is no stable pairing (i.e., disprove the
statement that for any set of preference lists given as input to the
general stable pairing problem, there is at least one stable
pairing). Hint: study the example on page 4 of the notes.
- Prove that the Traditional Marriage Algorithm must terminate
on the day that every girl has received a proposal.
- In class we argued that the Traditional Marriage Algorithm
will never require more than
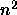 days to terminate. In fact,
it is possible to prove a tighter upper bound,
days to terminate. In fact,
it is possible to prove a tighter upper bound, 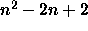 , on the maximum
number of days until the algorithm terminates.
, on the maximum
number of days until the algorithm terminates.
- Describe a set of preference
lists that requires
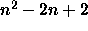 days to terminate.
days to terminate. - Extra Credit.
Prove that for any set of preference lists, it can take
no longer than
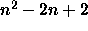 days until the algorithm terminates.
days until the algorithm terminates.
- Rosen, Section 3.3, Problem 6.
- Rosen, Section 3.3, Problem 12.
- Rosen, Section 4.1, problem 16.
- Rosen, Section 4.1, problem 34.



Next: About this document
Anna Karlin
Wed May 6 12:39:35 PDT 1998
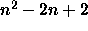 days to terminate.
days to terminate.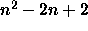 days until the algorithm terminates.
days until the algorithm terminates.