| Relation | reflexive? | symmetric? | antisymmetric? | transitive? |
|---|---|---|---|---|
| power2(x) = power2(y) | yes | yes | no | yes |
| power2(x) <= power2(y) | yes | no | no | yes |
| x mod 10 = y mod 10 | yes | yes | no | yes |
| x ⋅ y = 48 | no | yes | no | no |
| x ⋅ y = 1 | no | yes | yes | yes |
| 2 | (x - y) | yes | yes | no | yes |
| xy < 100 | no | no | no | no |
Solution: This is a straightforward application of Bayes' Rule. Let L represent the event that the bus is late and let C represent the event that Sam catches the bus. Then we are given the following probabilities:
- P(C|L) = 0.7
- P(C|¬L) = 0.2
- P(L) = 0.3
We also can infer that:
P(¬L) = 1 - P(L) = 1 - 0.3 = 0.7We want to compute the value of P(L|C). We do this using Bayes' Rule:
| P(L|C) | = P(C|L) ⋅ P(L) / (P(C|L) ⋅ P(L) + P(C|¬L) ⋅ P(¬ L)) |
| = 0.7 ⋅ 0.3 / (0.7 ⋅ 0.3 + 0.2 ⋅ 0.7) | |
| = 0.21 / 0.35 | |
| = 21/35 |
So the probability of the bus running late given that Sam caught it is 21/35.
Solution: Recall that you can compute the gcd of two integers using Euclid's algorithm:
5n + 4 = 1 ⋅ (4n + 3) + (n + 1)Thus, 1 is the greatest common divisor of 4n + 3 and 5n + 4, which is the definition of relatively prime.
4n + 3 = 3 ⋅ (n + 1) + n
n + 1 = 1 ⋅ n + 1
Being a slacker, Sam wants to do as little work as possible; he is looking for a way to reach every house without having to double back. Assume that once Sam passes a house (on either side of the street), then he can deliver mail to that house. Can Sam deliver mail to everyone without doubling back or retracing any of his steps? Why or why not?

Solution: We can model Squaresville perfectly as an undirected graph, in which the intersections of the streets are vertices, and the streets themselves are edges. If Sam delivers his mail without doubling back or retracing his steps, such a route must be an Euler path, since it requires crossing every edge exactly once. However, we know that an undirected graph with more than two vertices of odd degree cannot have an Euler path. In the map of Squaresville, all non-corner vertices on the edge of the map have odd degree, and hence no Euler path is possible. Sam cannot deliver his mail without doubling back or retracing his steps. If we require Sam to return back to the gate so he can go home, we can use a similar argument and show that there is no Euler circuit, because there are vertices with odd degrees.
Solution: First consider the case when n is even. The characters in the first half of the string can be freely chosen from the 26 letters, but the second half of the string must match the first half. Thus, we have (n/2) independent choices from the alphabet with duplicates allowed and where order matters. There are 26n/2 palindromes of even length.
If n is odd, then the method is the same, except that the middle character does not have a mirrored copy. It can be chosen freely, however. Thus, the total number of characters to be chosen is (n - 1)/2 + 1 = (n + 1)/2. Hence there are 26(n + 1)/2 palindromes of odd length.
- Consider the following relation over the set of sets.
R = {(A, B) | A ∩ B ≠ ∅}
Is R an equivalence relation? Why or why not?Solution: No. An equivalence relation is reflexive, symmetric, and transitive. Of the three, R is not transitive.
Let A = {1}, B = {1, 2}, and C = {2}. Note that A is related to B, and B is related to C, but A is not related to C.
- If so, let A = {1, 2, 3}. What is another set in the equivalence class of A? If not, leave this space blank.
- A pair of cubical (standard) dice are rolled together. A
player is paid $4 if the sum of the numbers is 10 or higher,
otherwise the player must pay $1. What is the expected payoff for
the player?
Solution: This is an expected value problem where the random variable represents the amount won or lost. The random variable takes on the value 4 when the two dice rolled add up to 10 or more and it takes on the value -1 otherwise. When two dice are rolled, there are 36 total outcomes, 6 of which lead to a sum greater than or equal to 10 (4/6, 5/5, 5/6, 6/4, 6/5, and 6/6). Thus, the probability of the random variable having the value 4 is 6/36 or 1/6. The probability of the random variable having value -1 is, thus, 5/6. And the expected value of the random variable is:
expected value = (1/6) ⋅ 4 + (5/6) ⋅ -1 = 4/6 - 5/6 = -1/6
- An octahedral die has eight (8) faces that are numbered 1 through
8. A dodecahedral die has twelve (12) faces that are numbered 1
through 12. What is the expected value of the sum of the numbers
that come up when a fair octahedral die and a fair dodecahedral die
are rolled together?
Solution: Let X1 be the value of the octahedral die and X2 be the value of the dodecahedral die. Let X be the sum of the numbers rolled (X = X1 + X2). By the linearity of expectation, E(X) = E(X1) + E(X2).
E(X1) = 1/8 ⋅ 1 + 1/8 ⋅ 2 + 1/8 ⋅ 3 + 1/8 ⋅ 4 + 1/8 ⋅ 5 + 1/8 ⋅ 6 + 1/8 ⋅ 7 + 1/8 ⋅ 8 = 1/8 ⋅ (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) = 1/8 ⋅ 36 = 4.5 Similarly,
E(X2) = 1/12 ⋅ (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) = 1/12 ⋅ 78 = 6.5 Thus, E(X) = 4.5 + 6.5 = 11.
Solution: We can prove this indirectly (proof by contrapositive). Assume that a = b and a = c. Then b = c. Since b = c, there cannot exist any m such that b is not congruent to c in modulo m. Every candidate m will divide b - c, which is 0, because every positive integer divides 0.
Solution: Suppose there are n people at the party. Every person can know between 1 and n - 1 other people. By the pigeonhole principle, two people must know the same number of other people.
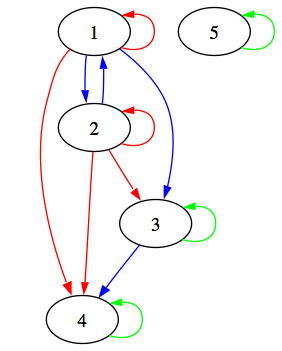
- Draw the graph of R.

- Draw the graph of the transitive closure of R.

- Draw the graph of the reflexive-transitive closure of R.
1/(1 ⋅ 3) + 1/(3 ⋅ 5) + 1/(5 ⋅ 7) + 1/(7 ⋅ 9) + ... + 1/((2n - 1)(2n + 1)) = n/(2n + 1)Provide a formal definition for the overall proposition being proved (P(n)) using summation notation and indicate the domain for n. Then provide an inductive proof, clearly indicating where you are applying the inductive hypothesis.
Let P(n) be the statement that:for n ∈ Z+.
n
∑
i = 11/((2i - 1)(2i + 1)) = n/(2n + 1) We first prove P(1):
1/(1 ⋅ 3) = 1 / 3 = 1 / (2 + 1) = 1 / (2 ⋅ 1 + 1)Then we assume P(k) for some k ∈ Z+:And we prove P(k + 1):
k
∑
i = 11/((2i - 1)(2i + 1)) = k/(2k + 1)
k + 1
∑
i = 11/((2i - 1)(2i + 1)) = (k + 1)/(2(k + 1) + 1) = (k + 1)/(2k +3)
k + 1
∑
i = 11/((2i - 1)(2i + 1)) = (by inductive hypothesis)
k
∑
i = 11/((2i - 1)(2i + 1)) + 1/((2k + 1)(2k + 3)) =
k/(2k + 1) + 1/((2k + 1)(2k + 3)) =
k(2k + 3)/((2k + 1)(2k + 3)) + 1/((2k + 1)(2k + 3)) =
(2k2 + 3k + 1)/((2k + 1)(2k + 3)) =
(2k + 1)(k + 1)/((2k + 1)(2k + 3)) =
(k + 1)/(2k + 3)
Therefore P(n) holds for all n ∈ Z+.
- In how many ways can the Treasury Department decide which five
candidates appear on the bills, without worrying about which bill
they will appear on? (An example choice is {a3,
a6, c3, c8,
d4}.)
Solution: This is a 5-combination of the 26 names (no duplicates allowed, order doesn't matter), so the answer is
C(26, 5)
- In how many ways can the Treasury department make the same choice
as in part (a) if they are required to choose at least one
candidate from each of the 4 categories?
Solution: We can choose one from each category and then choose a fifth person from the remaining people. This overcounts by a factor of 2 because it assumes that order matters for the two people chosen from the same category. So the number of ways to choose the five people is:
7 ⋅ 8 ⋅ 6 ⋅ 5 ⋅ 22 / 2
Alternatively, you could add up the various ways to pick 2 people from a given category and one from the other categories:C(7, 2) ⋅ 8 ⋅ 6 ⋅ 5 + 7 ⋅ C(8, 2) ⋅ 6 ⋅ 5 + 7 ⋅ 8 ⋅ C(6, 2) ⋅ 5 + 7 ⋅ 8 ⋅ 6 ⋅ C(5, 2)
These answers are equivalent. - If the Treasury chooses the candidates for the five bills
randomly, so that each sequence of five distinct candidates has
equal probability, what is the probability of the assignment
"c2 on $1, d4 on $5, b5 on $10,
c6 on $20, and a1 on $50"?
Solution: If chosen randomly, then each of the P(26, 5) permutations has equal probability of appearing. This particular permutation, then, has probability 1/P(26, 5) probability of appearing.
- If the Treasury chooses the candidates randomly as in part (c),
what is the probability that cartoon characters appear on the $5
and $10 bills but not on the $50 bill?
Solution: We must count how many permutations satisfy the given conditions. If cartoon characters are to appear on the $5 and $10 bills, we have a 2-permutation of those 6 names and then a 3-permutation of the remaining people:
P(6, 2) ⋅ P(24, 3)
But this would allow combinations where a cartoon character appears on the $50 bill, so we need to subtract those. Those cases involve a 3-permutation of the cartoon characters and a 2-permutation of the remaining names and we want to subtract that from our answer above:P(6, 2) ⋅ P(24, 3) - P(6, 3) ⋅ P(23, 2)
Therefore, the probability of this event is this number divided by the total number of permutations:(P(6, 2) ⋅ P(24, 3) - P(6, 3) ⋅ P(23, 2)) / P(26, 5)