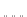- Define a set
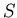 of character strings over the alphabet
of character strings over the alphabet
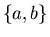 by the following rules:
by the following rules: 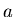 is in
is in 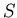 and
and 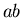 is in
is in 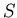 .
If the string
.
If the string  is in
is in 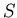 and
and 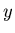 is in
is in 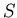 , then
, then 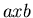 is in
is in 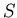 and
and 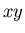 is in
is in 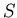 . Nothing else is in
. Nothing else is in 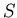 . Prove that every
string in
. Prove that every
string in 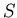 has at least as many
has at least as many 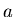 's as
's as 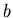 's.
's.
- Every day, starting on day 0, one vampire arrives in Seattle
from Transylvania and, starting on the day after its arrival, bites
one Seattlite every day. People bitten become vampires themselves
and live forever. New vampires also bite one person each day
starting the next day after they were bitten. Let
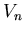 be the
number of vampires in Seattle on day
be the
number of vampires in Seattle on day 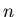 . So, for example,
. So, for example,  ,
,  (one that arrived from Transylvania on day 0, one that
he bit on day 1, and another one that arrived from Transylvania on
day 1),
(one that arrived from Transylvania on day 0, one that
he bit on day 1, and another one that arrived from Transylvania on
day 1), 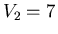 and so on.
and so on.
- Write a recurrence relation for
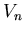 that is valid for any
that is valid for any  .
.
- Prove by induction on
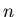 that
that 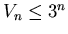 .
.
- Permutations:
- How many permutations of the letters {a,b,c,d,e,f,g,h} are
there?
- How many permutations of {a,b,c,d,e,f,g,h} are there that
don't contain the letters ``bad'' (appearing consecutively)?
- How many permutations of {a,b,c,d,e,f,g,h} are there that
don't contain either the letters ``bad'' appearing consecutively
or the letters ``fech'' appearing consecutively?
- How many words of length 10 can be constructed using the
letters {a,b,c,d,e,f,g,h} that contain exactly 3 a's? (They
don't have to have any English meaning.)
- A standard deck of 52 cards is shuffled completely (i.e., any of
the permutations is equally likely.) What is the probability that no
two spades are adjacent in the shuffled deck?
- Consider an undirected graph on
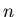 vertices generated as follows.
For each pair of vertices, an edge between those vertices is
included in the graph with probability
vertices generated as follows.
For each pair of vertices, an edge between those vertices is
included in the graph with probability  , and not included with
probability
, and not included with
probability  . What is the expected number of edges in the graph?
. What is the expected number of edges in the graph?
- Suppose a biased coin with probability 3/4 of coming up heads is
tossed independently 100 times.
- What is the conditional probability that the first 50 tosses
are heads given that the total number of heads is 50?
- What is the expected number of heads?
- Suppose that you are paid $50 if the number of heads in the
first two tosses is even and $100 if the number of heads in these
first two tosses is odd. What is your expected return?
- On the next set of questions, fill in the
 .
.
- The number of subsets of an
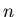 element set is
element set is 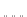
- The number of ways of choosing an unordered subset of size
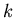 out of a set of size
out of a set of size 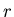 is
is 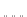
- The coefficient of
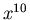 in the polynomial
in the polynomial 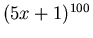 is
is 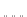
- The number of different binary relations from a set
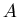 of size
of size
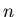 to a set
to a set 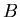 of size
of size  is
is 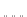
- The number of different reflexive binary relations on a set
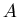 of size
of size 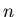 is
is 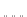
- The number of different undirected graphs (no self loops and
no parallel edges) on
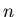 vertices is
vertices is 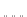
- The final exam of a discrete math course consists of 50
true/false questions, each worth two points, and 25 multiple-choice
questions, each worth four points. The probability that Linda
answers a true/false question correctly is 0.9, and the probability
that she answers a multiple-choice question correctly is 0.8. What
is her expected score on the final?
- A 3-person jury has two rational members, each of whom
independently has a probability p of making the correct decision,
and a third member who just flips a coin for each decision. The
majority decision rules. A one-person jury has probability p of
making the correct decision. Which jury has a better probability of
making the correct decision? Justify your answer.
- A pitcher's record is 21 wins and 4 losses. Prove that he must
have enjoyed a winning streak of 5 games.
Dieter Fox
2001-03-09
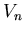 that is valid for any
that is valid for any  .
.
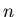 that
that 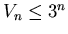 .
.
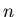 element set is
element set is 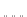
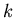 out of a set of size
out of a set of size 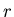 is
is 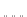
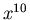 in the polynomial
in the polynomial 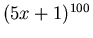 is
is 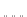
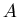 of size
of size
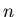 to a set
to a set 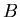 of size
of size  is
is 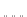
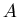 of size
of size 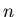 is
is 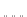
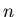 vertices is
vertices is