THA4 - Networks

Useful CSE 163 Resources¶

• CSE 163 Code Quality Guide
• Common Python Errors
• Common THA Errors
• flake8 References
• Testing Tips

Learning objective: Work with graph data structures using networkx, implement social network analysis algorithms, and practice object-oriented programming through class inheritance.

You can find the starter code here. Make sure to extract (unzip) the contents anywhere on your computer. If you are working in VS Code, navigate to File | Open or Open Folder, then select the hw4 folder.

• hw4_analysis.py and hw4_graphs.py are the files for you to put your implementations of the Technical Component.

• hw4_creative.ipynb is the notebook for you to complete the Creative Component

• verify_setup.py is a test file to make sure that networkx has been installed successfully. Do not modify this file!

• facebook-links.txt and facebook-links-small.txt are text files which will be converted to a graph in analysis.py for you to write your recommendation algorithm.

• facebook-links-small-output.txt is the expected printed output after running the complete and working algorithm on facebook-links-small.txt. Do not modify this file!

Context¶

Social networks are everywhere in our digital lives. Whether it’s following friends on Instagram, connecting with colleagues on LinkedIn, or subscribing to creators on YouTube, these platforms fundamentally operate as graphs: collections of nodes (people, accounts) connected by edges (relationships, follows, friendships).

Understanding social networks through the lens of graph theory opens up powerful possibilities for analysis. For instance, how do platforms decide which new accounts to recommend you follow? How can we identify influential users in a network? How do communities form within larger social structures? These questions can all be answered using graph algorithms.

In this assignment, you’ll work with Python’s networkx library, a powerful tool for creating, analyzing, and manipulating graph data structures. You’ll start by building simple social network graphs, then implement two different recommendation algorithms that platforms like Twitter, Instagram, and LinkedIn might use to suggest new connections. The first algorithm prioritizes quantity (how many mutual connections you share), while the second prioritizes quality (how selective those mutual connections are).

Installing networkx¶

Before starting this assignment, you’ll need to install the networkx library in your Python environment. There are two ways to do this. If you already have networkx installed in your cse163 environment, you can skip this step!

If you are installing for the first time, either or both of these methods might take a while to run. This is expected and normal!

Using Anaconda Navigator¶

1. In Anaconda Navigator, navigate to the Environments tab and select cse163.
2. Above the list of packages, you will find a search bar. Select the dropdown menu to search for “Not installed” packages, and search for networkx here.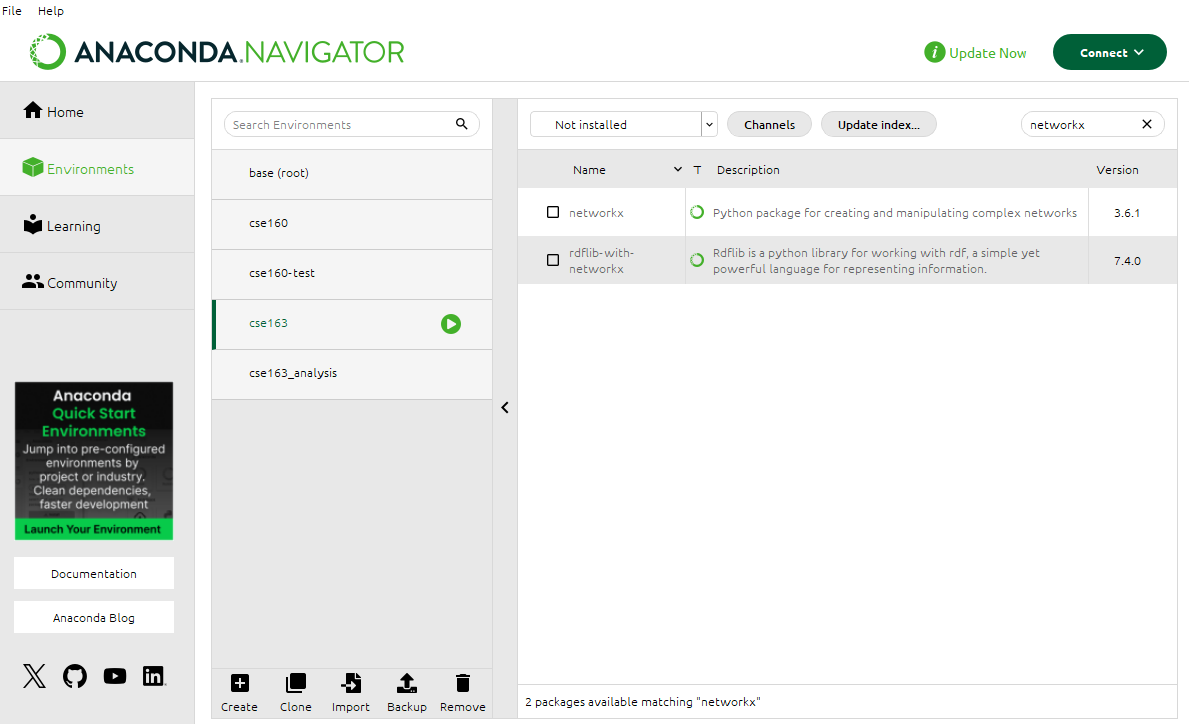
3. Select the checkmark next to networkx and then click “Apply”. You may run into other pop-ups asking to confirm or apply the installation. Make sure to click “Apply” or “Confirm” each time.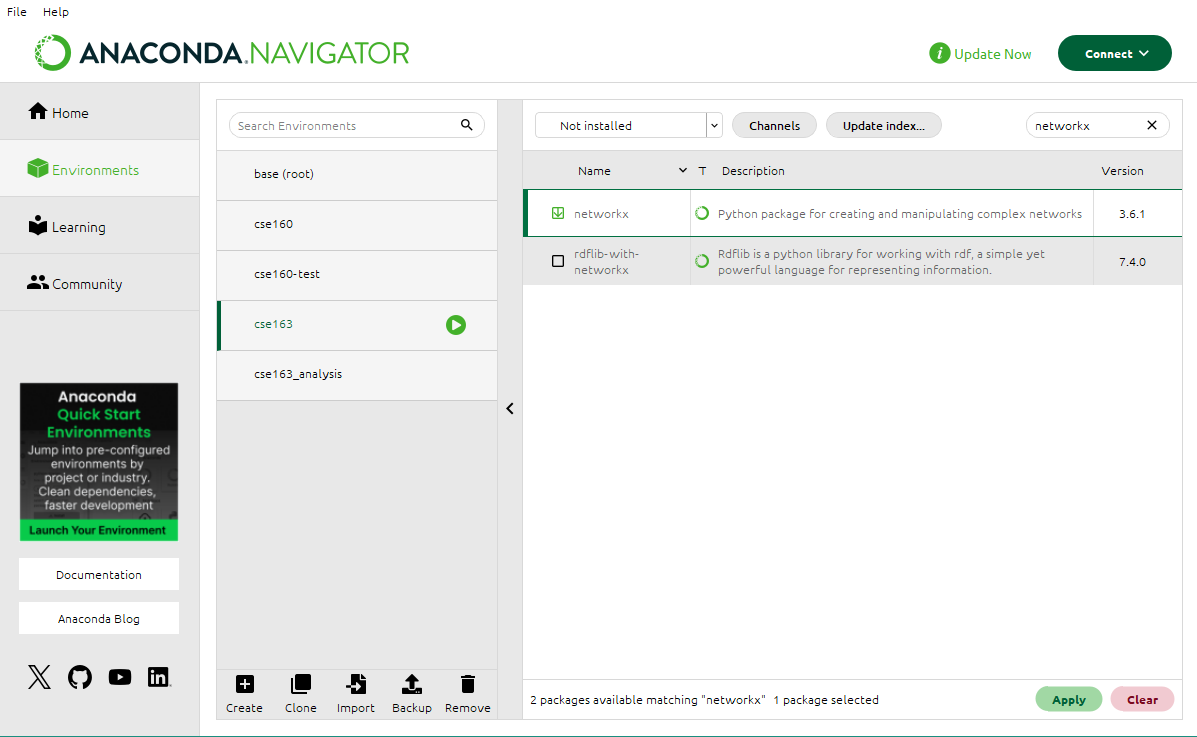

Using conda in a Terminal¶

1. Open a terminal.
2. If the cse163 environment is not already activated, type conda activate cse163 into the terminal and hit Return/Enter.
3. Type conda install networkx into the terminal and hit Return/Enter.

Verify Setup¶

Open verify_setup.py and run this file. In your terminal, you will see the output string "Networkx was installed correctly!", and you should see a three-node graph saved to test_graph.png:

Technical Component¶

hw4_graphs.py¶

In hw4_graphs.py, you will practice drawing a Graph and a Digraph. You may use the networkx tutorial as a reference; any function or syntax up to the end of the section titled “Directed Graphs” may be used in this THA.

Practice Graph¶

Task: Write a function get_practice_graph() that creates and returns the following graph and saves it to a file practice_graph.png. Note that this graph is here for illustrative purposes, and the exact output of your graph may vary. Use the Graph class (not DiGraph, MultiGraph, or MultiDiGraph).

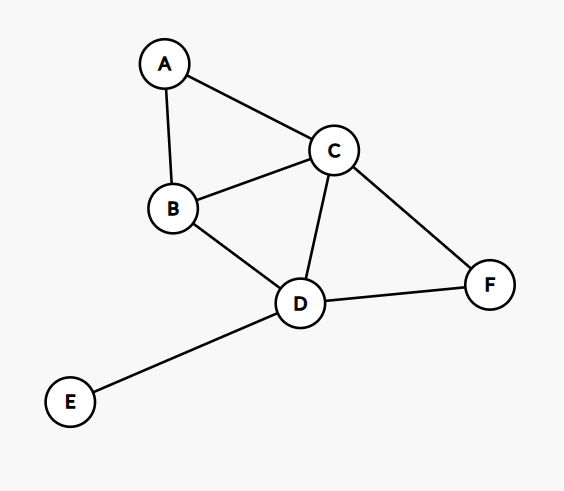
The graph should contain 6 nodes labeled A through F with the following edges:

• A connects to: B, C
• B connects to: A, C, D
• C connects to: A, B, D, F
• D connects to: B, C, E, F
• E connects to: D
• F connects to: C, D

Your function get_practice_graph() should return the graph itself. In main, save your graph with plt.savefig('practice_graph.png').

Practice DiGraph¶

Task: Write a function get_practice_digraph() that creates and returns the following graph and saves it to a file practice_digraph.png. Note that this graph is here for illustrative purposes, and the exact output of your graph may vary. Use the DiGraph class (not Graph, MultiGraph, or MultiDiGraph).

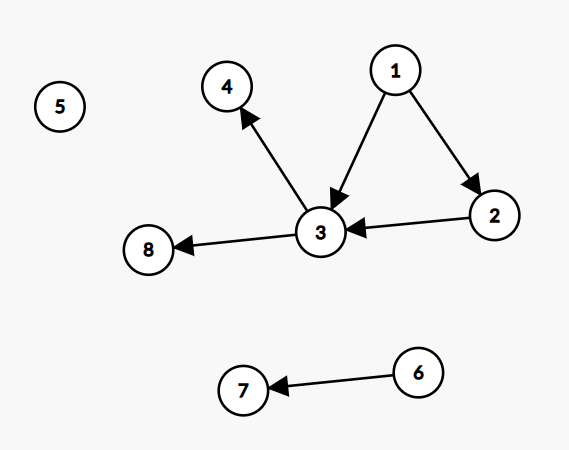
The graph should contain 8 nodes labeled 1 through 8 with the following edges:

• 1 has directed edges to 2 and 3
• 2 has a directed edge to 3
• 3 has a directed edge to 4 and 8
• 6 has a directed edge to 7
• 5 has no directed edges

Your function get_practice_digraph() should return the graph itself. In main, save your graph with plt.savefig('practice_digraph.png').

hw4_analysis.py¶

When you sign into a social media site like Facebook, it suggests friends. In this part of the THA, you will write a program that reads Facebook data and makes friend recommendations. As a concrete example, consider “A” in practice_graph (pictured again below). Suppose we are interested in giving person “A” recommendations of people that they might want to be friends with. By this algorithm, the number of friends you have in common with someone is a measure of how likely it is that they would be a good friend recommendation for you. Therefore, the more friends someone has in common with you, the better their “friendship score” is. We will use the number of friends in common as the friendship score itself.

In this case, we want to find out who has friends in common with “A”.

• A has one friend in common with B (namely, C), but A and B are already friends, so we would not recommend B.
• A has one friend in common with C (namely, B), but A and C are already friends, so we would not recommend C.
• A has two friends in common with D (namely, B and C).
• A has no friends in common with E, so we would not recommend E.
• A has one friend in common with F (namely, C).

Because D has two mutual friends with A, D has a friendship score of 2 making D the top recommendation for A. Using the same logic, F is the second best recommendation. We would not recommend B or C because A is already friends with them. We also would not recommend E because A has no friends in common with E.

Now, let us think about how we might create this list. We will need to calculate these “friendship scores” for some set of people in the graph. Because we are using “number of common friends” as our metric, we only care about calculating scores for people who are friends of X’s current friends and not currently a friend of X. There could be many people in a large graph, so we do not want to calculate friendship scores for every person in the graph. Many of those scores will likely be zero because they do not share any friends with X.

Because of this, we will need to calculate the set of “friends-of-friends” for user X. For each of those friends-of-friends, we will calculate the set of friends that they have in common with X. If we want to give user X a ranked list of recommendations from best to worst, then it would be useful to have a data structure to keep track of the mapping of “friend of friend” to friendship score. Finally, given this mapping of people to friendship scores, we will want to sort the potential friends from best to worst before presenting it to the user.

To implement this algorithm, we’ll write the following functions.

Note: The helper functions read_facebook(), friends() and friends_of_friends() have already been defined for you in analysis.py. Make sure you understand what these functions do!

common_friends¶

Task: Write a function common_friends which takes in the Facebook graph object and two users, user1 and user2, and then returns the set of friends that user1 and user2 have in common.

Hint: You may find set operations like &, |, or - helpful here.

recs_by_common_friends¶

Task: Write a function recs_by_common_friends which takes in the Facebook graph and a user, then returns a list of friend recommendations, sorted by the number of common friends. The list only contains people who have at least one friend in common with the given user and are neither the user nor one of the user’s friends.

Sorting rules: The list is sorted from most common friends to fewest. When two people have the same number of common friends, they are sorted by their natural sort order from least to greatest.

Example: Given a graph my_graph and user "X":

• "X" and "Y" have two friends in common
• "X" and "Z" have one friend in common
• "X" and "W" have one friend in common
• "X" and "V" have no friends in common
• "X" is friends with "W" (but not with "Y" or "Z")

recs_by_common_friends(my_graph, "X")  =>  ['Y', 'Z']

recs_by_influence¶

Task: Write a function recs_by_influence which takes in the Facebook graph and a user, then returns a list of friend recommendations for the given user, sorted by influence score. The list only contains people who have at least one friend in common with the given user and are neither the user nor one of the user’s friends.

Influence score is computed by summing, over each common friend, the reciprocal of that common friend’s total number of friends. Consider the following purely hypothetical situation:

• Two of your friends are Margaret Hamilton and Anita Borg.
• Anita Borg has only two friends (you and one other person).
• Margaret Hamilton has 7 billion friends.
• Anita and Margaret have no friends in common (besides you).

Since Anita is highly selective in terms of friendship, and is a friend of yours, you are likely to have a lot in common with Anita’s other friend. On the other hand, Margaret has so many friends that there is little reason to believe that you should be friendly with any particular one of Margaret’s other friends.

Incorporate the above idea into your friend recommendation algorithm. We call this technique influence scoring.

Suppose that user1 and user2 have three friends in common: f1, f2, and f3. In the recommendation by common friends, the score for user2 as a friend of user1 is $1+1+1$. Each common friend contributes 1 to the score.

With influence scoring, the score for user2 as a friend of user1 now becomes:

$\frac{1}{\tt{numfriends(f1)}} + \frac{1}{\tt{numfriends(f2)}} + \frac{1}{\tt{numfriends(f3)}}$

where $\tt{numfriends(f)}$ evaluates to the number of friends that $\tt{f}$ has. In other words, each friend X of user1 has a total influence score of 1 to contribute, which is divided equally among all of X‘s friends.

In the example above, Anita’s one other friend would have a score of ½, and each of Margaret Hamilton’s friends would have a score of 1/7000000000.

Sorting rules: The list is sorted from highest influence score to lowest. When two people have the same influence score, they are sorted by their natural sort order from least to greatest.

Facebook Analysis¶

The heart of our analysis will go directly into main. The Facebook data has already been read in for you as a graph, courtesy of the read_facebook function. Now, you need to apply both recs_by_common_friends and recs_by_influence to the Facebook data. However, the dataset is quite large, so let’s only look at the users who have ids which are a multiple of 1000.

Task: For every Facebook user with a user id that is a multiple of 1000, print a list containing the first 10 friend recommendations, as determined by “number of common friends” friendship score. If there are fewer than 10 recommendations, print all the recommendations. This is a sample of part of what you would expect for your output—you should be printing more lines than this, and they should be listed in ascending order of userID as shown below (e.g. user 28000, followed by user 29000, etc.):

...
 28000 (by num_common_friends): [23, 1445, 4610, 7996, 10397, 11213, 56, 85, 471, 522]
 29000 (by num_common_friends): [28606]
 30000 (by num_common_friends): [862, 869, 919, 941, 3154, 8180, 8269, 8614, 14473, 14495]
...

Task: For every Facebook user with a user id that is a multiple of 1000, print a list containing the first 10 friend recommendations as determined by the “influence” friendship score. If there are fewer than 10 recommendations, print all the recommendations. This is a sample of part of what you would expect for your output:

...
28000 (by influence): [7033, 17125, 15462, 33049, 51105, 16424, 23, 7996, 725, 1539]
29000 (by influence): [28606]
30000 (by influence): [862, 869, 919, 941, 3154, 8269, 14473, 14495, 17951, 19611]
...

Task: Does the recommendation algorithm make a difference for Facebook? Considering only those 63 Facebook users with an id that is a multiple of 1000, compute and print the number of Facebook users who have the same first 10 friend recommendations under both recommendation systems, and the number of Facebook users who have different first 10 friend recommendations under the two recommendation systems.

For example, in the data above, user 29000 has the same first ten recommendations under both recommendation systems, while user 28000 and user 30000 both have different recommendations under the two recommendation systems. This program may take some time to compute (possibly a minute or so) depending on the efficiency of your solution.

Your output from main should look like the following, but with ellipses and blanks replaced by actual numbers:

Recommendations by common friends:

...
____ (by num_common_friends): [____, ____, ...]
____ (by num_common_friends): [____, ____, ...]
____ (by num_common_friends): [____, ____, ...]
...

Recommendations by influence:

...
____ (by influence): [____, ____, ...]
____ (by influence): [____, ____, ...]
____ (by influence): [____, ____, ...]
...

Difference in Algorithm Recommendations: ____

Ellipses (...) indicate that there may be more of these lines, and underscores (____) should be replaced by values that you will calculate. For the recommendations, each line may have a different number of values than what is shown above, and you will be printing more than 3 lines of output—these are just examples.

Creative Component: Getting Classy¶

So far, we’ve explored networkx‘s graph classes to model social media networks. But graphs can be used to represent many more applications!

Task: Choose one of the following network types and create a custom class that inherits from it so that you can represent a different kind of network:

• Graph
• DiGraph
• MultiGraph
• MultiDiGraph

Here are some ideas for the different kinds of graphs you might extend:

• A professional network like LinkedIn where nodes represent users who have attributes like jobs, proficiencies, skills, whether they’re currently employed, etc.
• A transit system where nodes represent different transportation modes which have attributes like route, duration, fare, location, etc.
• A prerequisite map where nodes represent different courses that have attributes like credit hours, department, number, section, time, etc.
• A food web where nodes represent species who have attributes like diet, habitat, count, etc.

Note: You are not required to implement one of these options! You can use them as inspiration, but your final class must be your own!

Requirements¶

In the following code cell, define your new class which extends one of the four graph options above. Your class must meet the following requirements:

• At least 2 new node attributes
• At least 3 new class methods (i.e., not overriding an existing graph method)
• All fields type-annotated
• All functions type-annotated and documented

Then, show us your class in action! Create an instance of your class, add some nodes to it, and demonstrate each of your new functions. You are not responsible for testing with assert statements in this part of the THA, but you should make sure that your output is visible after running the code cells.

At the end of the provided notebook, describe your approach to creating this class. What made you choose this particular extension, node attributes, and functions? How do you imagine this class might be used?

Quality¶

Assessment submissions should pass these checks: flake8 and code quality guidelines. The code quality guidelines are very thorough. For this assessment, the most relevant rules can be found in these sections (new sections bolded):

• Naming

• Documentation

• Efficiency and Redundancy

• Classes

  • Class Comment

  • Private Fields

• Type Annotations

Submission¶

Submit your work by uploading the following files to Gradescope:

• hw4_analysis.py

• hw4_graphs.py

• hw4_creative.ipynb

• practice_graph.png

• practice_digraph.png

You may find it helpful to download all your files from VS Code and save them as a zip file. If you are working locally, there are a few options for creating a zip file. You can right-click a folder and compress it to zip. Or you can select the entire folder contents and compress them to a zip.

You can upload the zip file directly to Gradescope, and it will extract the files for you. Submit as often as you want until the deadline for the initial submission. Note that we will only grade your most recent submission.

Please make sure you are familiar with the resources and policies outlined in the syllabus and the take-home assessments page.

THA 4 - Networks

Initial Submission by Thursday 02/12 at 11:59 pm.

Submit on Gradescope