Model Evaluation

In this lesson, we'll learn how to evaluate the quality of a machine learning model. By the end of this lesson, students will be able to:

• Apply get_dummies to represent categorical features as one or more dummy variables.
• Apply train_test_split to randomly split a dataset into a training set and test set.
• Evaluate machine learning models in terms of overfit and underfit.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

import pandas as pd

Dummy variables

Last time, we tried to predict the price of a home from all the other variables. However, we learned that since the city column contains categorical string values, we can't use it as a feature in a regression algorithm.

homes = pd.read_csv("homes.csv")
homes

	beds	bath	price	year_built	sqft	price_per_sqft	elevation	city
0	2.0	1.0	999000	1960	1000	999	10	NY
1	2.0	2.0	2750000	2006	1418	1939	0	NY
2	2.0	2.0	1350000	1900	2150	628	9	NY
3	1.0	1.0	629000	1903	500	1258	9	NY
4	0.0	1.0	439000	1930	500	878	10	NY
...	...	...	...	...	...	...	...	...
487	5.0	2.5	1800000	1890	3073	586	76	SF
488	2.0	1.0	695000	1923	1045	665	106	SF
489	3.0	2.0	1650000	1922	1483	1113	106	SF
490	1.0	1.0	649000	1983	850	764	163	SF
491	3.0	2.0	995000	1956	1305	762	216	SF

492 rows × 8 columns

This problem not only occurs when using DecisionTreeRegressor, but it also occurs when using LinearRegression since we can't multiply a categorical string value with a numeric slope value. Let's learn how to represent these categorical features as one or more dummy variables.

def model_parameters(reg, columns):
    """Returns a string with the linear regression model parameters for the given column names."""
    slopes = [f"{coef:.2f}({columns[i]})" for i, coef in enumerate(reg.coef_)]
    return " + ".join([f"{reg.intercept_:.2f}"] + slopes)

X = pd.get_dummies(homes.drop("price", axis=1))
y = homes["price"]
reg = LinearRegression().fit(X, y)

print("Model:", model_parameters(reg, X.columns))
print("Error:", mean_squared_error(y, reg.predict(X)))

Model: 2667451.86 + -91657.73(beds) + -46672.61(bath) + -2986.99(year_built) + 1611.73(sqft) + 2563.08(price_per_sqft) + -1081.63(elevation) + -173696.89(city_NY) + 173696.89(city_SF)
Error: 976495129525.2129

X.columns

Index(['beds', 'bath', 'year_built', 'sqft', 'price_per_sqft', 'elevation',
       'city_NY', 'city_SF'],
      dtype='object')

reg.coef_

array([ -91657.73070027,  -46672.60578863,   -2986.9928551 ,
          1611.73147091,    2563.07698129,   -1081.6314029 ,
       -173696.88763047,  173696.88763047])

X

	beds	bath	year_built	sqft	price_per_sqft	elevation	city_NY	city_SF
0	2.0	1.0	1960	1000	999	10	True	False
1	2.0	2.0	2006	1418	1939	0	True	False
2	2.0	2.0	1900	2150	628	9	True	False
3	1.0	1.0	1903	500	1258	9	True	False
4	0.0	1.0	1930	500	878	10	True	False
...	...	...	...	...	...	...	...	...
487	5.0	2.5	1890	3073	586	76	False	True
488	2.0	1.0	1923	1045	665	106	False	True
489	3.0	2.0	1922	1483	1113	106	False	True
490	1.0	1.0	1983	850	764	163	False	True
491	3.0	2.0	1956	1305	762	216	False	True

492 rows × 8 columns

Overfitting

In our introduction to machine learning, we explained that the researchers who worked on calibrating the PurpleAir Sensor (PAS) measurements against the EPA Air Quality Sensor (AQS) measurements ultimately decided to use the model that included only the PAS and humidity features (variables)—ignoring the opportunity to use the temperature and dew point even though a model that includes all features produced a lower overall mean squared error.

sensor_data = pd.read_csv("sensor_data.csv")
sensor_data

	AQS	temp	humidity	dew	PAS
0	6.7	18.027263	38.564815	3.629662	8.616954
1	3.8	16.115280	49.404315	5.442318	3.493916
2	4.0	19.897634	29.972222	1.734051	3.799601
3	4.7	21.378334	32.474513	4.165624	4.369691
4	3.2	18.443822	43.898226	5.867611	3.191071
...	...	...	...	...	...
12092	5.5	-12.101337	54.188889	-19.555834	2.386120
12093	16.8	4.159967	56.256030	-3.870659	32.444987
12094	15.6	1.707895	65.779221	-4.083768	25.297018
12095	14.0	-14.380144	48.206481	-23.015378	8.213208
12096	5.8	5.081813	52.200000	-4.016401	9.436011

12097 rows × 5 columns

X = sensor_data.drop("AQS", axis=1)
y = sensor_data["AQS"]
reg = LinearRegression().fit(X, y)

print("Model:", model_parameters(reg, X.columns))
# squared=False for RMSE: root mean squared error
print("Error:", mean_squared_error(y, reg.predict(X), squared=False))

Model: 7.11 + -0.03(temp) + -0.08(humidity) + 0.03(dew) + 0.43(PAS)
Error: 2.267367483110072

sum((y - reg.predict(X))**2)/len(..)

y - reg.predict(X) # mg/m3
(y - reg.predict(X))**2 # (mg/m3)^2
sum((y - reg.predict(X))**2) # (mg/m3)^2
sum((y - reg.predict(X))**2) / len(..) # (mg/m3)^2
sqrt(sum((y - reg.predict(X))**2) / len(..)) # mg/m3

X = sensor_data[["PAS", "humidity"]]
y = sensor_data["AQS"]
reg = LinearRegression().fit(X, y)

print("Model:", model_parameters(reg, X.columns))
# squared=False for RMSE: root mean squared error
print("Error:", mean_squared_error(y, reg.predict(X), squared=False))

Model: 6.25 + 0.43(PAS) + -0.07(humidity)
Error: 2.268198812569166

The unit of PM2.5 is µg/m^3 (microgram per cubic meters).

Poll question: what is the unit of the RMSE?

In fact, the authors (Barkjohn et al. 2021) tested the impact of incrementally introducing a feature to the model to determine which combination of features could provide the most useful model—not necessarily the most accurate one. In their research, they aimed to predict the PAS measurement from the AQS measurement, the opposite of our task, and they included interactions between features indicated by the × symbol. For each grouping of models with a certain number of features, they highlighted the model with the lowest root mean squared error (RMSE, or the square root of the MSE) using an asterisk *.

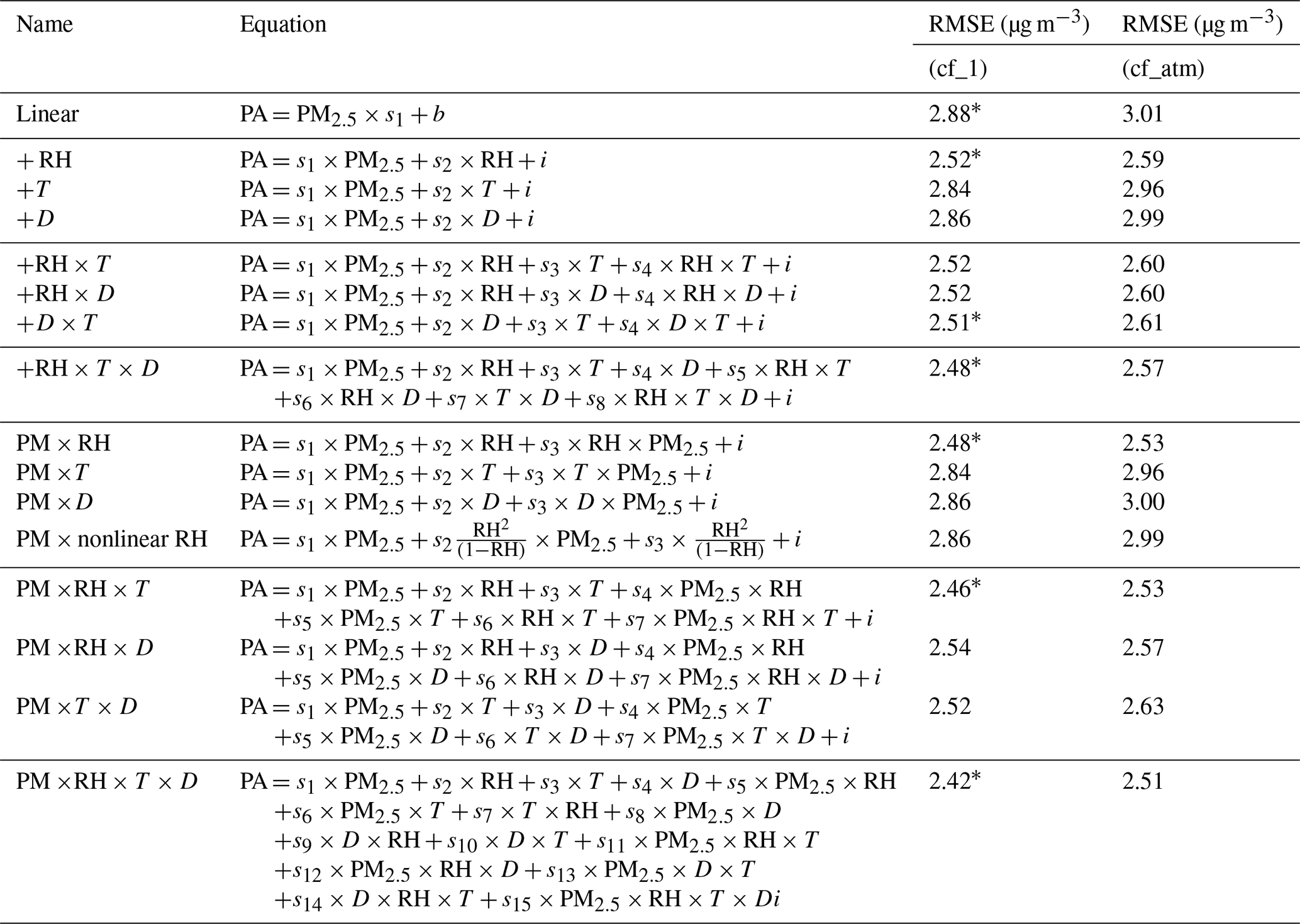
The model at the bottom of the table that includes all the features also has the lowest RMSE loss. But the loss value alone is not a convincing measure: adding more features into a model not only leads to a model that is harder to explain, but also increases the possibility of overfitting.

A model is considered overfit if its predictions correspond too closely to the training dataset such that improvements reported on the training dataset are not reflected when the model is run on a testing dataset (or in the real world). To simulate training and testing datasets, we can take our X features and y labels and subdivide them into X_train, X_test, y_train, y_test using the train_test_split function. The testing dataset should only be used during final model evaluation when we're ready to report the overall effectiveness of our final machine learning model.

from sklearn.model_selection import train_test_split

# test_size=0.2 indicates 80% training dataset and 20% testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# During model training, use only the training dataset
reg = LinearRegression().fit(X_train, y_train)

print("Model:", model_parameters(reg, X_train.columns))
# During model evaluation, use the testing dataset
print("Error on training:", mean_squared_error(y_train, reg.predict(X_train), squared=False))
print("Error on testing:", mean_squared_error(y_test, reg.predict(X_test), squared=False))

Model: 7.07 + -0.02(temp) + -0.08(humidity) + 0.02(dew) + 0.43(PAS)
Error on training: 2.2540060701228097
Error on testing: 2.320334517845879

Feature selection

Feature selection describes the process of selecting only a subset of features in order to improve the quality of a machine learning model. In the air quality sensor calibration study, we can begin with all the features and gradually remove the least-important features one-by-one.

features = ["PAS", "humidity"]

reg = LinearRegression().fit(X_train.loc[:, features], y_train)
print("Model:", model_parameters(reg, features))
print("Error:", mean_squared_error(y_test, reg.predict(X_test.loc[:, features]), squared=False))

Model: 6.28 + 0.43(PAS) + -0.07(humidity)
Error: 2.3212571520123144

reg.coef_

array([ 0.42751047, -0.07048322, -0.0031819 ])

Recursive feature elimination (RFE) automates this process by starting with a model that includes all the variables and removes features from the model starting with the ones that contribute the least weight (smallest coefficients in a linear regression).

from sklearn.feature_selection import RFE

# Remove 1 feature per step until half the original features remain
# here 0.5 is the percentage
# we can use numbers like 1, 2, 3, 4 as well
rfe = RFE(LinearRegression(), step=1, n_features_to_select=0.5, verbose=1)
rfe.fit(X_train, y_train)

# Show the final subset of features
rfe_features = X.columns[[r == 1 for r in rfe.ranking_]]
print("Features:", list(rfe_features))

# Extract the last LinearRegression model trained on the final subset of features
reg = rfe.estimator_

print("Model:", model_parameters(reg, rfe_features))
print("Error:", mean_squared_error(y_test, rfe.predict(X_test), squared=False))

Fitting estimator with 4 features.
Fitting estimator with 3 features.
Features: ['humidity', 'PAS']
Model: 6.28 + -0.07(humidity) + 0.43(PAS)
Error: 2.3212571520123144

Cross validation

How do we know when to stop removing features during feature selection? We can certainly use intuition or look at the changes in error as we remove each feature. But this still requires us to evaluate the model somehow. If the testing dataset can only be used at the end of model evaluation, it was wrong of us to use the testing dataset during feature selection!

Cross-validation provides one way to help us explore different models before we choose a final model for evaluation at the end. Cross-validation lets us evaluate models without touching the testing dataset by introducing new validation datasets.

The simplest way to cross-validate is to call the cross_val_score helper function on an unfitted machine learning algorithm and the dataset. This function will further subdivide the training dataset into 5 folds and, for each of the 5 folds, train a separate model on the training folds and evaluate them on the validation fold.

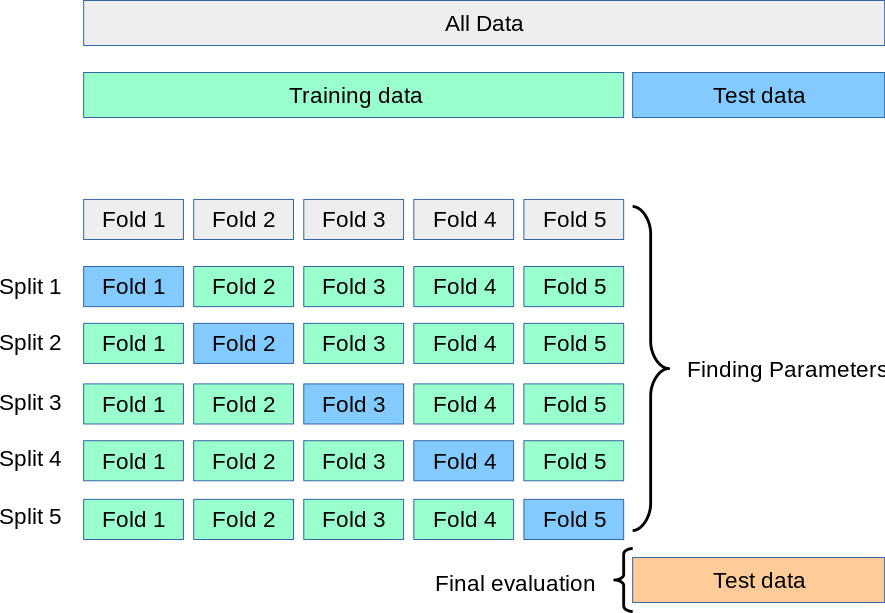
The scoring parameter can accept the string name of a scorer function. Higher (more positive) scores are considered better, so we use the negative RMSE value as the scorer function.

from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor

cross_val_score(
    estimator=DecisionTreeRegressor(max_depth=2),
    X=X_train,
    y=y_train,
    scoring="neg_root_mean_squared_error",
    verbose=3,
)

[CV] END ............................... score: (test=-3.102) total time=   0.0s
[CV] END ............................... score: (test=-2.980) total time=   0.0s
[CV] END ............................... score: (test=-2.804) total time=   0.0s
[CV] END ............................... score: (test=-3.355) total time=   0.0s
[CV] END ............................... score: (test=-2.944) total time=   0.0s

array([-3.10241248, -2.98034944, -2.80424655, -3.35492307, -2.94449081])

As we've seen throughout these lessons on machine learning, we prefer to automate our processes. Rather than modify the max_depth and manually tweaking the values until we find something that works, we can use GridSearchCV to exhaustively search all hyperparameter options. Here, the first 5 folds for max_depth=2 are exactly the same as cross_val_score.

from sklearn.model_selection import GridSearchCV

search = GridSearchCV(
    estimator=DecisionTreeRegressor(),
    param_grid={"max_depth": [2, 3, 4, 5, 6, 7, 8, 9, 10]},
    scoring="neg_root_mean_squared_error",
    verbose=3,
)
search.fit(X_train, y_train)

# Show the best score and best estimator at the end of hyperparameter search
print("Mean score for best model:", search.best_score_)
reg = search.best_estimator_
print("Best model:", reg)

Fitting 5 folds for each of 9 candidates, totalling 45 fits
[CV 1/5] END ......................max_depth=2;, score=-3.102 total time=   0.0s
[CV 2/5] END ......................max_depth=2;, score=-2.980 total time=   0.0s
[CV 3/5] END ......................max_depth=2;, score=-2.804 total time=   0.0s
[CV 4/5] END ......................max_depth=2;, score=-3.355 total time=   0.0s
[CV 5/5] END ......................max_depth=2;, score=-2.944 total time=   0.0s
[CV 1/5] END ......................max_depth=3;, score=-2.896 total time=   0.0s
[CV 2/5] END ......................max_depth=3;, score=-2.797 total time=   0.0s
[CV 3/5] END ......................max_depth=3;, score=-2.596 total time=   0.0s
[CV 4/5] END ......................max_depth=3;, score=-3.141 total time=   0.0s
[CV 5/5] END ......................max_depth=3;, score=-2.651 total time=   0.0s
[CV 1/5] END ......................max_depth=4;, score=-2.607 total time=   0.0s
[CV 2/5] END ......................max_depth=4;, score=-2.546 total time=   0.0s
[CV 3/5] END ......................max_depth=4;, score=-2.389 total time=   0.0s
[CV 4/5] END ......................max_depth=4;, score=-2.585 total time=   0.0s
[CV 5/5] END ......................max_depth=4;, score=-2.357 total time=   0.0s
[CV 1/5] END ......................max_depth=5;, score=-2.507 total time=   0.0s
[CV 2/5] END ......................max_depth=5;, score=-2.453 total time=   0.0s
[CV 3/5] END ......................max_depth=5;, score=-2.321 total time=   0.0s
[CV 4/5] END ......................max_depth=5;, score=-2.516 total time=   0.0s
[CV 5/5] END ......................max_depth=5;, score=-2.293 total time=   0.0s
[CV 1/5] END ......................max_depth=6;, score=-2.427 total time=   0.0s
[CV 2/5] END ......................max_depth=6;, score=-2.401 total time=   0.0s
[CV 3/5] END ......................max_depth=6;, score=-2.247 total time=   0.0s
[CV 4/5] END ......................max_depth=6;, score=-2.432 total time=   0.0s
[CV 5/5] END ......................max_depth=6;, score=-2.181 total time=   0.0s
[CV 1/5] END ......................max_depth=7;, score=-2.392 total time=   0.0s
[CV 2/5] END ......................max_depth=7;, score=-2.344 total time=   0.0s
[CV 3/5] END ......................max_depth=7;, score=-2.227 total time=   0.0s
[CV 4/5] END ......................max_depth=7;, score=-2.462 total time=   0.0s
[CV 5/5] END ......................max_depth=7;, score=-2.461 total time=   0.0s
[CV 1/5] END ......................max_depth=8;, score=-2.423 total time=   0.0s
[CV 2/5] END ......................max_depth=8;, score=-2.365 total time=   0.0s
[CV 3/5] END ......................max_depth=8;, score=-2.205 total time=   0.0s
[CV 4/5] END ......................max_depth=8;, score=-2.435 total time=   0.0s
[CV 5/5] END ......................max_depth=8;, score=-2.221 total time=   0.0s
[CV 1/5] END ......................max_depth=9;, score=-2.523 total time=   0.0s
[CV 2/5] END ......................max_depth=9;, score=-2.379 total time=   0.0s
[CV 3/5] END ......................max_depth=9;, score=-2.267 total time=   0.0s
[CV 4/5] END ......................max_depth=9;, score=-2.378 total time=   0.0s
[CV 5/5] END ......................max_depth=9;, score=-2.265 total time=   0.0s
[CV 1/5] END .....................max_depth=10;, score=-2.549 total time=   0.0s
[CV 2/5] END .....................max_depth=10;, score=-2.450 total time=   0.0s
[CV 3/5] END .....................max_depth=10;, score=-2.266 total time=   0.0s
[CV 4/5] END .....................max_depth=10;, score=-2.563 total time=   0.0s
[CV 5/5] END .....................max_depth=10;, score=-2.603 total time=   0.0s
Mean score for best model: -2.329791435660566
Best model: DecisionTreeRegressor(max_depth=8)

Finally, we can report the test error for the best model by evaluating it against the testing dataset. Why is the testing dataset error different from the mean score for the best model printed above?

print("Error:", mean_squared_error(y_test, reg.predict(X_test), squared=False))

Visualizing decision tree models

Last time, we plotted the predictions for a linear regression model that was trained to take PAS measurements and predict AQS measurements. What do you think a decision tree model would look like for this simplified PurpleAir sensor calibration problem?

Here's a complete workflow for decision tree model evaluation using the practices above. The resulting plot compares a linear regression model lmplot against the decisions made by a decision tree.

# Split dataset into 80% training dataset and 20% testing dataset
X = sensor_data.drop("AQS", axis=1)
y = sensor_data["AQS"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Recursive feature elimination to select the single most important feature based on slope value
rfe = RFE(LinearRegression(), n_features_to_select=1, verbose=1)
rfe.fit(X_train, y_train)
# Print the best feature to predict AQS
rfe_feature = X.columns[rfe.ranking_.argmin()]
print("Best feature to predict AQS:", rfe_feature)
# Use only the best feature
X = X[[rfe_feature]]
X_train = X_train[[rfe_feature]]
X_test = X_test[[rfe_feature]]

# Grid search cross-validation to tune the max_depth hyperparameter using RMSE loss metric
search = GridSearchCV(
    estimator=DecisionTreeRegressor(),
    param_grid={"max_depth": [2, 3, 4, 5, 6, 7, 8, 9, 10]},
    scoring="neg_root_mean_squared_error",
    verbose=3,
)
search.fit(X_train, y_train)
# Print the best score and best estimator at the end of hyperparameter search
print("Mean score for best model:", search.best_score_)
reg = search.best_estimator_
print("Best model:", reg)

# During model evaluation, use the testing dataset
print("Test error:", mean_squared_error(y_test, search.predict(X_test), squared=False))

# Visualize the tree decisions compared to a LinearRegression model (lmplot)
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.tree import plot_tree
sns.set_theme()
grid = sns.lmplot(sensor_data, x=rfe_feature, y="AQS")
# Create a demonstration dataset that counts from 0 to the max PAS value
X_demo = pd.DataFrame(np.arange(X[rfe_feature].max()), columns=[rfe_feature])
grid.facet_axis(0, 0).plot(X_demo, reg.predict(X_demo), c="orange")
grid.set(title=f"lmplot vs {reg}")
# Show nodes in the decision tree
plt.figure(dpi=300)
plot_tree(
    reg,
    max_depth=2, # Only show the first two levels
    linewidth=3,
    feature_names=[rfe_feature],
    label="root",
    filled=True,
    impurity=False,
    proportion=True,
    rounded=False
) and None # Hide return value of plot_tree

The testing dataset error rates for both the DecisionTreeRegressor and the LinearRegression models are not too far apart. Which model would you prefer to use? Justify your answer using either the error rates below or the visualizations above.

print("Tree error:", mean_squared_error(y_test, search.predict(X_test), squared=False))
print("Line error:", mean_squared_error(
    y_test,
    LinearRegression().fit(X_train, y_train).predict(X_test),
    squared=False
))

Earlier, we discussed how overfitting to the testing dataset can be mitigated by using cross-validation. But in answering the previous question on whether we should prefer a DecisionTreeRegressor model or a LinearRegression model, we've actually overfit the model by hand! Explain how preferring one model over the other according to the visualization overfits to the testing dataset.