CSE 163, Spring 2020: Homework 6: Processing Image Data

Learning Objectives

After this homework, students will be able to:

• Read in an image into a program from a file.
• Work with numpy arrays to perform computations.
• Read a technical description of an algorithm and implement it in code.

Expectations

Here are some baseline expectations we expect you to meet:

• Follow the course collaboration policies

• You do not need to write any tests for this assignment, but you may find doing so helpful!

Part 0 Expectations

• For this part of the assignment, you may import and use the numpy, imageio, and matplotlib.pyplot packages, but you may not use any other imports to solve this problem.
• While we have talked about that it is generally best to avoid loops if possible when working with our data science libraries, this problem set may require using some loops. For each problem, we will specify the number of loops you may use when solving the problem. By "loop", we mean any python loop or comprehension in the code you write.
• Some of these problems will only work with gray-scale images (2-d numpy arrays) while others will work with color images (3-d numpy arrays). Each problem will specify which type of image your solution should handle and you do not need to handle the other for that problem.
• All of these functions should be written in hw6_main.py.

Problem 0: invert_colors

Input: A color image represented as a 3-d numpy array.

Write a function called invert_colors that takes a color image and returns a new color image with all the colors "inverted". An inverted image changes each color channel so that if there was a high value for a color at a pixel, the result will have a low value instead for that channel. The specifics of the inversion is, for each color channel, to subtract the pixel value from the number 255; if there was a high value (near 255), then it will become small after this computation and vice versa. The result of this function should be returned as a numpy array.

You may use no loops to solve this problem. Everything should be done using numpy computations. This method should NOT modify the input parameter, but rather should return a new numpy array.

For example, if we were to call this function passing in the array for images/puppy.png and plotting the result, we would see:

Problem 1: blur

Input: A gray-scale image represented as a 2-d numpy array and a number specifying the size of the "patch" (described below).

Write a function called blur that takes a gray-scale image and the patch size and returns a new image that has been blurred using the given patch size. This is essentially a convolution where we are using a kernel with width and height of the patch size, where we take the average of all the values that overlap with the kernel at each iteration. This is equivalent to doing a convolution with a kernel of this size, where all the values are \(\frac{1}{patch\_size^2}\). The return should be a new numpy array that stores the averages values from the convolution casted to ints. Below are two example calls, one that shows a very small example that can be done by hand and the second an actual image with different patch sizes.

You will need to convert the values in the resulting matrix to integers so it can be plotted properly. To do this, you can convert numpy array of floats to a numpy array of integers. Assuming you have a numpy array of floats stored in a variable called result, you can create a new array of ints with the line result.astype(np.uint8).

You may use two loops to solve this problem (to move the sliding window). Everything else should be done using numpy computations. This method should NOT modify the input parameters, but rather should return a new numpy array.

Example Blur on Small Image

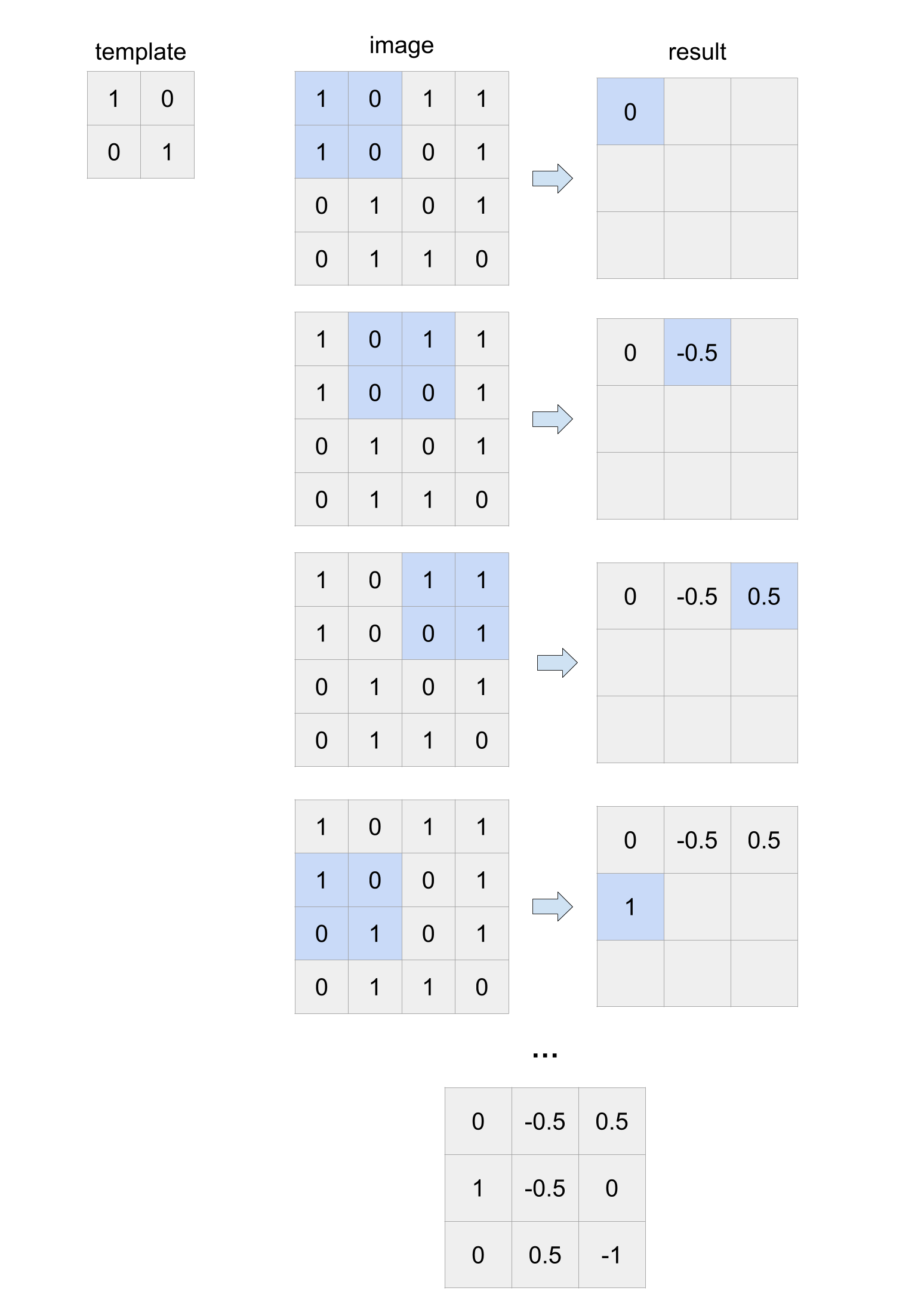
This shows the steps of computation for blurring a 4x4 image using a patch size of 2. The 3x3 matrix at the bottom would be the returned value. Notice the blurred image is actually smaller because it's not able to keep all of the boundary pixels.

Example Blur on Puppy Image

Here is the result of blurring a real image of a puppy.

Using a patch size of 10.

Using a patch size of 30.

Development Strategy:

• Figure out the size of the result image based on the input image and patch size. Note that the image may not be square, but by our definition the patch must be square.
• Write the actual code to do the convolution traversal and computing the mean of the image subset at each step.

Problem 2: template_match

Input: A gray-scale image represented by a 2-d numpy array and a smaller gray-scale image represented by a 2-d numpy array.

For this problem, we will be implementing a common task of finding the instance of a small image in a larger image. For example, we might have an image of a specific coin (the template) and an image of many coins and we want to find where the coin appears in this larger image. At a high level, this algorithm works like a convolution over the image using the template as the kernel, where it computes a "similarity measure" between the template and the current portion of the image. The result returned should be the similarities at each possible point, which our provided code will use to find the most likely spot by finding the position with maximum similarity.

The similarity measure we will use is based on the idea of a "cross correlation". For each position of the template in the algorithm, we will compute the sum of element-wise product between the current section of the image and the template (much like a step of a convolution). However, we don't want to use the raw pixel values since high brightness can cause artificially high similarities. Instead, we have to "de-mean" both the template and the section of the image we are currently looking at by subtracting their average pixel values from all their respective pixels. At a pseudo-code level, this involves for each valid position of the template over the image:

1. Compute the relevant section of the image we want to look at, we will call this "current" in the remaining steps.
2. Subtract the mean pixel value in current from each pixel in current.
3. Subtract the mean pixel value in the template from each pixel in the template.
4. Compute the correlation by multiplying each pixel from the de-meaned current with its corresponding pixel in the de-meaned template. Add all these values up to compute the similarity.

This is shown as an example in the expandable box below with some concrete numbers to make it more clear.

This function should return a 2-d numpy array of floats that stores the similarity between the template at each valid point in the image. You should NOT round or cast the array to integers. You should see the last problem for an appropriate development strategy.

You may use two loops to solve this problem (to move the sliding window). Everything else should be done using numpy computations. This method should NOT modify the input parameters, but rather should return a new numpy array.

Example template_match on small image

Below shows the steps of computing the result for a small image with a small template. Some things to note about the example.

• Neither the image or the template will necessarily be a square. If the template was a different size, the result will be a different size too.
• For simplicity, all the pixel values are 0 or 1, but this will not be the case in general since a gray-scale image can have any value between 0 and 255.
• The output numbers in this example are between 1 and -1, but this is not true in general. To find the match, we would search for the highest number in the result.
• For this example, you should NOT round or cast the outputs. We just happened to get precise answers for this example.

Notice in the second step, the result is -0.5. This is because the mean pixel value of that section of the image is 0.25 while the mean pixel value for the template is 0.5 which leaves the similarity as: \[ (0 - 0.25) * (1 - 0.5) + (1 - 0.25) * (0 - 0.5) + (0 - 0.25) * (0 - 0.5) + (0 - 0.25) * (1 - 0.5) = -0.5\]

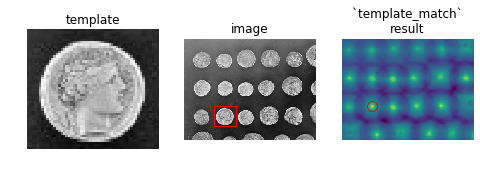
Example template_match on real images

Using coins.png and using a template coins[170:220, 75:130]

Using gray_puppy.png and using a template gray_puppy[150:200, 175:225]

Using gray_puppy.png and using a template gray_puppy[355:435, 200:276]

You can create these plots by using the following method we defined that makes these plots for the given image, template, and result of template_match. You do not need to include these in your solution, but you may do so!

def find_xy(result):
    """
    Given the result of template_match, finds the position (x, y) with
    the highest similarity.
    """
    ij = np.unravel_index(np.argmax(result), result.shape)
    return ij[::-1]


def plot_result(image, template, result, output_file='match.png'):
    """
    Given an image, a template, and the result of
    template_match(image, template), makes a plot showing the result
    of the match.

    Saves result to given file path
    """
    x, y = find_xy(result)

    plt.figure(figsize=(8, 3))
    ax1 = plt.subplot(1, 3, 1)
    ax2 = plt.subplot(1, 3, 2)
    ax3 = plt.subplot(1, 3, 3, sharex=ax2, sharey=ax2)

    ax1.imshow(template, cmap=plt.cm.gray)
    ax1.set_axis_off()
    ax1.set_title('template')

    ax2.imshow(image, cmap=plt.cm.gray)
    ax2.set_axis_off()
    ax2.set_title('image')
    # highlight matched region
    template_height,  template_width = template.shape
    rect = plt.Rectangle((x, y), template_width, template_height,
                         edgecolor='r', facecolor='none')
    ax2.add_patch(rect)

    ax3.imshow(result)
    ax3.set_axis_off()
    ax3.set_title('`template_match`\nresult')
    # highlight matched region
    ax3.autoscale(False)
    ax3.plot(x, y, 'o', markeredgecolor='r', markerfacecolor='none',
             markersize=10)
    plt.savefig(output_file)