Homework 4: K-Means Clustering

Part I Due: at 11:59pm on Tuesday, February 8, 2022. Submit via Gradescope. (REQUIRED Feedback Survey)
Part II Due: at 11:59pm on Monday, February 14, 2022. Submit via Gradescope. (REQUIRED Feedback Survey)

Learning Objectives:

Videos:

This time we have a couple videos available to help clarify the assignment. We highly recommend watching these videos before starting, or if you are confused about the content.

The following link goes to a folder containing two videos covering part 1 and 2 of the homework as well as general tips for completing the homework. Additionally, it covers topics in the background section, such as the K-means algorithm, with specific examples. The direct link for these videos is here.

The videos will also be embedded here:

Part 1:

Part 2:

Introduction

In Homework 4, we will implement a commonly-used algorithm: K-means clustering. (Read more about K-means on the K-means Wikipedia page if you're interested). K-means is a popular machine learning and data mining algorithm that discovers potential clusters within a dataset. Finding these clusters in a dataset can often reveal interesting and meaningful structures underlying the distribution of data. K-means clustering has been applied to many problems in science and still remains popular today for its simplicity and effectiveness. Here are a few examples of recently published papers using K-means:

Hopefully, these examples motivate you to try this homework out! You will very likely be able to apply this computational tool to some problems relevant to you! We will break down the name and explain the algorithm now.

Background: Data, Distances, Clusters and Centroids

Data

We will assume we have a dataset of m data points where each data point is n-dimensional. For example, we could have 100 points on a two dimensional plane, then m = 100 and n = 2.

Euclidean Distance

Given two n-dimensional points a and b where:



we define the distance between points a and b as:

This is commonly known as the Euclidean distance. For example, if we had the three-dimensional points x1 and x2 defined as Python lists: 

x1 = [-2, -1, -4]
x2 = [10, -5, 5]

Then the Euclidean distance would be calculated as:

Here is another example with two four-dimensional points: 

x1 = [0, 0, 1, 1]
x2 = [1, 1, 0, 0]
And its Euclidean distance calculation:

Clusters

A cluster is a collection of points that are part of the same group. For k-means, every point has a cluster that it is part of. As the algorithm progresses, points may change what cluster they are currently in, even though the point itself does not move.

For instance, all blue points are part of cluster1, all red points are part of cluster2, all green points are part of cluster3

Centroids

A centroid can be seen as the "center of mass" of a group of points. In K-means, we assume that the centroid of a cluster is the mean of all the points in that cluster. The mean data point consists of the mean of the components on each dimension. Say, for three n-dimensional points a, b, and c, we have the mean as:

For example, if a cluster contains three 2D points (displayed as Python lists) as below: 

x1 = [1, 1]
x2 = [2, 3]
x3 = [3, 2]
The centroid for this cluster is defined as: 
c = [(1 + 2 + 3)/3, (1 + 3 + 2)/3] # evaluates to [2, 2]

The following image is a graphical representation of what these three points and their centroid would look like

K-means

Our ultimate goal is to partition the data points into K clusters. How do we know which data point belongs to which cluster? In K-means, we assign each data point to the cluster whose centroid is closest to that data point.

Let's assume we already have K centroids, initialized randomly. Now, if our randomly initialized centroids were already in good locations, we would have been done! However, it is most likely that the initial centroid locations do not reflect any information about the data (since they were just random). To update the centroid locations to something that makes more sense we use an iterative approach:

  1. First, we assign all data points to their corresponding centroids by finding the centroid that is closest.
  2. Then, we adjust the centroid location to be the average of all points in that cluster.

We iteratively repeat these two steps to achieve better and better cluster centroids and meaningful assignments of data points.

Note that the data points do not change! Only the location of the centroids change with each iteration (and thus the points that are closest to each centroid changes).

The following images are an example of a single run of the K-means algorithm:

K-means Convergence

One last question you may have is, when do we stop repeating these two steps? I.e., what does it mean for the algorithm to have converged? We say the algorithm has converged if the locations of all centroids did not change much between two iterations. (ex. Within 1 * 10-5 or 0.00001)

Take this example of two centroids of 2-dimensional points. If at the previous iteration, we have the two centroid locations as: 

c1 = [0.45132, -0.99134]
c2 = [-0.34135, -2.3525]
And at the next iteration the centroids are updated to: 
c1 = [1.43332, -1.9334]
c2 = [-1.78782, -2.3523]
Then we say the algorithm has NOT converged, since the location of the two centroids are very different between iterations. However, if the new locations of the centroids are instead: 
c1 = [0.45132, -0.99134]
c2 = [-0.34135, -2.3524]
Then we say the algorithm HAS converged, since the locations of the two centroids are very similar between iterations (Typically, "very similar" means for every dimension of two points a and b, their difference (|a - b|) is smaller than some constant (1 * 10-5 or 0.00001 is a common choice)).

The Algorithm

In summary, the K-means algorithm (in pseudo code) is described as follows: 

data = Load Data
centroids = Randomly Created K Centroids
while centroids not converged:
    for each data point:
        assign data point to the closest centroid
    for each centroid:
        set new centroid location to be the mean of 
        all points in this cluster

The following gif visualizes this process, and will be what you accomplish in Part 1! The initial frame (step0) is the initialization: two randomly chosen centroids are drawn as an X in blue (centroid 0) and red (centroid 1). Then in the following steps (step1 through step6):

  1. First, data points are assigned to whichever centroid is closest (and colored accordingly),
  2. Then centroid locations are adjusted based on the mean of all red/blue points.
This process is repeated until the centroids do not move anymore. Notice how in the later steps the centroids do not move as much between steps as they do in the earlier steps.

Notice how the data points never move, but they may be assigned (be closest to) different centroids as the centroids move. As different points are assigned to a different centroid, the average of all points assigned to a centroid may change, moving the centroid. The algorithm stops/converges when the centroids are not quite moving (or move very little between iterations).

You can also check out Naftali Harris's Visualizing K-Means Clustering site to play with k-means and get more familiar with it.

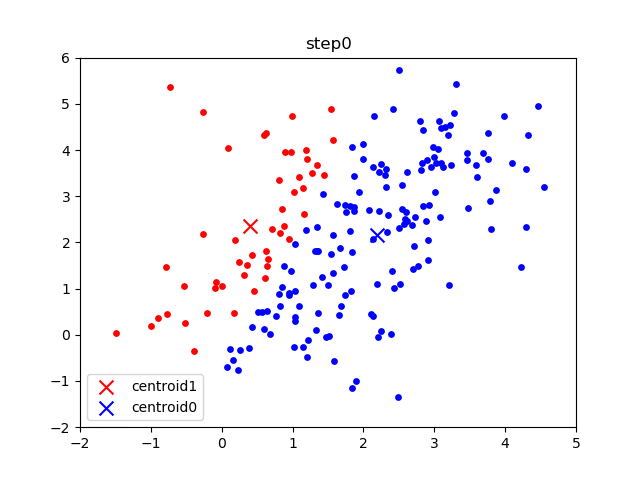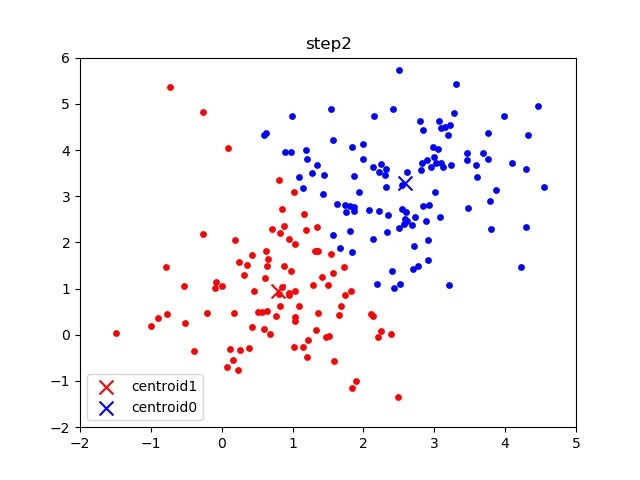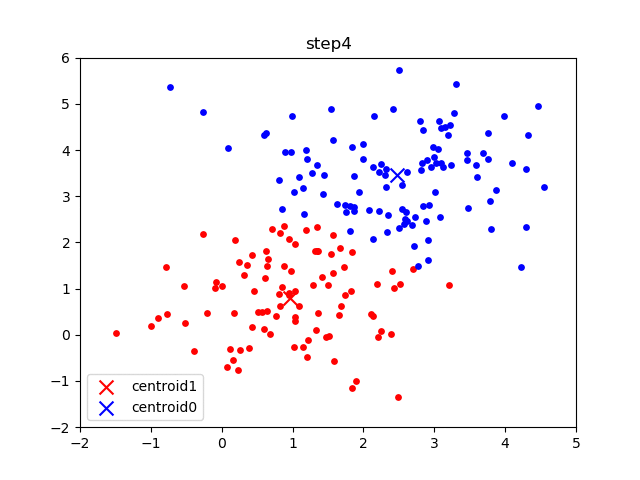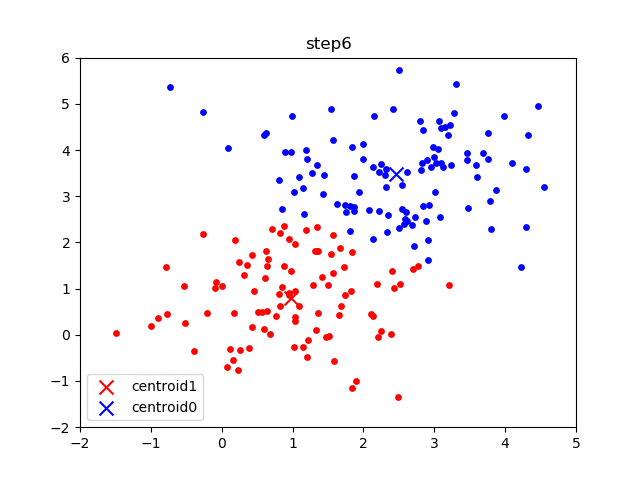
In the following parts of this homework, you will implement this algorithm and apply it to (1) 2D points shown in the gif above; (2) a small subset of the MNIST hand-written digit dataset.

Part 0: Getting Started

Download homework4.zip and unzip the file to get started. You should see the following file structure in the homework4 folder: 

homework4
├── analysis.py [Your code for Part 2]
├── data [data to run the programs with]
│   ├── 2d_init_centroids.csv
│   ├── data_2d.csv
│   ├── mnist.csv
│   └── mnist_init_centroids.csv
├── kmeans.py [Your code for Part 1 and Part 2]
├── results [Where your result figures will be saved]
│   ├── 2D
│   └── MNIST
│       ├── final
│       └── init
└── utils.py [Helper code: Don't edit]

The red highlighted parts are where you will work on your code. We have provided utils.py which contains helper code to help you complete the assignment. Do not change anything in utils.py!

Part 1: Implementing the Algorithm

You will be given the following data structures for K-means clustering:

Step 1: Calculating Euclidean distances

Implement the following function in kmeans.py: 

def euclidean_distance(point1, point2):
    """Calculate the Euclidean distance between two data points.

    Arguments:
        point1: a non-empty list of floats representing a data point
        point2: a non-empty list of floats representing a data point

    Returns: the Euclidean distance between two data points

    Example:
        Code:
            point1 = [1.1, 1, 1, 0.5]
            point2 = [4, 3.14, 2, 1]
            print(euclidean_distance(point1, point2))
        Output:
            3.7735394525564456
    """

If you want more information on what Euclidean distance is, re-read the Euclidean distance background section in the spec and/or the Euclidean distance Wikipedia page. In the code we have provided you for this (and all functions you need to implement), the body of the function is empty. We have provided testing code for you to verify your implementation. Run 

python kmeans.py
in a terminal window to verify your implementation of euclidean_distance. If you passed our tests, you should see: 
test_euclidean_distance passed.
Note that you may find several assertions further down in the program failing at this point. This is to be expected since you have not implemented those parts of the program yet! In fact this will continue to happen as you progress through the problems. Success usually means you are no longer failing the same assertion, but that instead a different assertion is failing further down in the program.

Step 2: Assigning data points to closest centroids

Implement the following function in kmeans.py: 

def get_closest_centroid(point, centroids_dict):
    """Given a datapoint, finds the closest centroid. You should use
    the euclidean_distance function (that you previously implemented).

    Arguments:
        point: a list of floats representing a data point
        centroids_dict: a dictionary representing the centroids where the keys
                        are strings (centroid names) and the values are lists
                        of centroid locations

    Returns: a string as the key name of the closest centroid to the data point

    Example:
        Code:
            point = [0, 0, 0, 0]
            centroids_dict = {"centroid1": [1, 1, 1, 1],
                            "centroid2": [2, 2, 2, 2]}
            print(get_closest_centroid(point, centroids_dict))
        Output:
            centroid1
    """

If you want more information on centroids, check out the Centroids section in the spec. We have provided testing code for you to verify your implementation. test_closest_centroid() is already set up to run when 

python kmeans.py
is typed in a terminal window. Check the output of this test to verify your implementation.

Step 3: Update assignment of points to centroids

Implement the following function in kmeans.py: 

def update_assignment(list_of_points, centroids_dict):
    """
    Assign all data points to the closest centroids. You should use
    the get_closest_centroid function (that you previously implemented).

    Arguments:
        list_of_points: a list of lists representing all data points
        centroids_dict: a dictionary representing the centroids where the keys
                        are strings (centroid names) and the values are lists
                        of centroid locations

    Returns: a new dictionary whose keys are the centroids' key names and
             values are lists of points that belong to the centroid. If a
             given centroid does not have any data points closest to it,
             do not include the centroid in the returned dictionary.

    Example:
        Code:
            list_of_points = [[1.1, 1, 1, 0.5], [4, 3.14, 2, 1], [0, 0, 0, 0]]
            centroids_dict = {"centroid1": [1, 1, 1, 1],
                                        "centroid2": [2, 2, 2, 2]}

            print(update_assignment(list_of_points, centroids_dict))
        Output:
            {'centroid1': [[1.1, 1, 1, 0.5], [0, 0, 0, 0]],
             'centroid2': [[4, 3.14, 2, 1]]}
    """

Notice that your algorithm should run regardless of if any centroid becomes empty, i.e. there are no points that are the closest to a centroid. In that case you should not include that centroid in the dictionary you return.

We have provided testing code for you to verify your implementation. test_update_assignment() is already set up to run when 

python kmeans.py
is typed in a terminal window. Check the output of this test to verify your implementation.

Step 4: Update centroids

Implement the following function in kmeans.py: 

def mean_of_points(list_of_points):
    """Calculate the mean of a given group of data points. You should NOT
    hard-code the dimensionality of the data points.

    Arguments:
        list_of_points: a list of lists representing a group of data points

    Returns: a list of floats as the mean of the given data points

    Example:
        Code:
            list_of_points = [[1.1, 1, 1, 0.5], [4, 3.14, 2, 1], [0, 0, 0, 0]]
            print(mean_of_points(list_of_points))
        Output:
            [1.7, 1.3800000000000001, 1.0, 0.5]
    """

Notice that you should not hard-code the dimensionality of data - your code needs to run regardless of the dimension of data!

We have provided testing code for you to verify your implementation. test_mean_of_points() is already set up to run when 

python kmeans.py
is typed in a terminal window. Check the output of this test to verify your implementation. A common error students make when implementing this function is to modify the provided list of points. Be sure your implementation does not modify the provided list of points.

Now implement the following function in kmeans.py: 

def update_centroids(assignment_dict):
    """
    Update centroid locations as the mean of all data points that belong
    to the cluster. You should use the mean_of_points function (that you
    previously implemented).
    
    Arguments:
        assignment_dict: the dictionary returned by update_assignment function
    
    Returns: A new dictionary representing the updated centroids
    """

Notice that you should not hard-code the dimensionality of data - your code needs to run regardless of the dimension of data!
We have provided testing code for you to verify your implementation. test_update_centroids() is already set up to run when 

python kmeans.py
is typed in a terminal window. Check the output of this test to verify your implementation.

You have now completed all parts needed to run your k-means algorithm! As a sanity check, try running everything together one more time by typing: 
python kmeans.py
in the terminal window. You should see: 
All tests passed.

Step 5: Clustering 2D points

You have now completed all parts needed to run your k-means algorithm! Now, let's verify your implementation by running the algorithm on 2D points. At the bottom of kmeans.py you should see code like this: 

if __name__ == "__main__":
    main_test()

    # data, label = read_data("data/data_2d.csv")
    # init_c = load_centroids("data/2d_init_centroids.csv")
    # final_c = main_2d(data, init_c)
    # write_centroids_tofile("2d_final_centroids.csv", final_c)

This is the code that actually runs when you run this file. Right now your code is only calling the main_test() function. De-comment the last four lines and turn the call to main_test() into a comment. These new commands will load the 2D data points and the initial centroids we provided in from .csv files. After that, main_2d will execute the k-means algorithm and write_centroids_tofile will save the final centroids to a file to save them permanently. Your code should now look like this: 

if __name__ == '__main__':
    # main_test()

    data, label = read_data("data/data_2d.csv")
    init_c = load_centroids("data/2d_init_centroids.csv")
    final_c = main_2d(data, init_c)
    write_centroids_tofile("2d_final_centroids.csv", final_c)

Now run your program again by typing 

python kmeans.py
in the terminal window. If you are successful, you should see: 
K-means converged after 7 steps.
as the output of the program. In addition, there should be 7 plots generated, in the results/2D/ folder. If you examine these 7 plots, they should be identical to the steps shown in the the gif shown in the algorithm section of this spec.

Step 6: Submit!

You've completed part 1! Before you take a break, be sure to submit kmeans.py via Gradescope. To ensure your program produces the correct output, you should make the code at the bottom of your kmeans.py look identical to what we described in Step 5.

Answer a REQUIRED survey asking how much time you spent and other reflections on this part of the assignment.

Part 2: Another dataset & Analyzing the Performance

Trying the Algorithm on MNIST

Now that you have successfully run K-means clustering on 2-dimensional data points with 2 centroids, we will use your code to do clustering of 784-dimensional data points with 10 centroids. Don't worry, you won't need to change any of the code that you wrote!

We will apply the algorithm to a real world data set known as the Modified National Institute of Standards and Technology database (MNIST). It is a dataset that consists of images of hand-written digits. Here are nine example images from the MNIST data set (we are using a very small subset of all MNIST images):

Each of these images is 28 pixels by 28 pixels, for a total of 784 pixels. (As in HW3, pixels have values between 0 and 255 (0=black, 255=white), although we don't need to know this for K-means.) Each image can be thought of as a 784-dimensional data point, represented as a list containing 784 numbers. For the images shown above, many of the numbers would be zero since the image is mostly black. So the nine sample images above are actually nine sample data points!

We will see how applying K-means to these digit images helps us discover clusters of images which contain mostly one kind of digit!

To load the MNIST dataset instead of the 2D points, change the code at the bottom of the file to the following (the red text shows the changes that should be made): 

if __name__ == '__main__':
    # main_test()

    data, label = read_data("data/mnist.csv")
    init_c = load_centroids("data/mnist_init_centroids.csv")
    final_c = main_mnist(data, init_c)
    write_centroids_tofile("mnist_final_centroids.csv", final_c)

You should leave the rest of your code intact, and it should run with the new data without errors! Run this command again (it may take a minute to run on this data set!): 

python kmeans.py

You should see the following output: 

K-means converged after 18 steps.
Meanwhile, in the results/MNIST folder, the init and final folders should be filled with the centroids plotted as images. Remember that centroids are basically a data point that represents the average of all the data points (images) that are assigned to it.

In the init folder, the centroids should look like static/random pixels (left below), because that's how we randomly initialized them. In the final folder, they should look like actual digits (right below), assuming similar data points (images) have been clustered together!



This shows that K-means has adjusted the locations of the centroids from our random initialization to a more meaningful space that corresponds to where the MNIST data is distributed. By just looking at this centroid, can you guess which digit this cluster might contain the most images of? Regardless, this shows that our algorithm can not only learn clusters, but also adapt to different datasets -- from the 2D example in Part 1 to the 784-dimensional data space of the MNIST images.

Analyzing the Performance

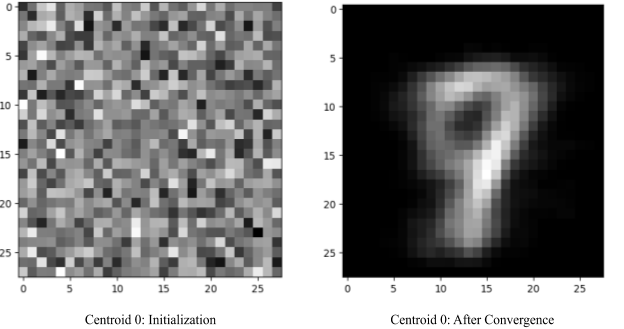
How do we evaluate the performance of our algorithm? The images in the MNIST data set have been labelled with the digit they actually represent. (You can see this label as the digit in the first column on each row in the file mnist.csv. Each row of that file represents one data point (image).) So, one way to evaluate our algorithm would be to examine the accuracy of the classification of the images from MNIST. For example, how many of the images known to be (labelled as) the digit 4 ended up in the centroid we think of as representing the digit 4?

First, let's define the "classifications" of our data points provided by K-means. We take a majority-takes-all approach: we assign each cluster a label as the majority labels of all data points in this cluster. For example, say we have data points with these labels assigned to cluster1: 

2, 2, 2, 2, 2, 2, 8, 6, 2, 2, 6, 8, 8, 2, 2
Since there are 10 2's, 3 8's, and 2 6's, we say the label of cluster 1 is 2 since it's the majority label. (i.e The first six images have a label of 2, the seventh image has a label of 8, the eighth image has a label of 6)

We define the accuracy of the classification for a centroid as:

In the example above, the majority label is 2, there are 10 label 2's, and there are 15 labels in total. So we say the accuracy for cluster1 is: and we consider the labels that are not the majority label in a cluster as errors.

We can repeat this step for all clusters and derive the accuracy measure of the algorithm. For every cluster, we first figure out what the majority label is for that cluster, and keep track of the count of the majority labels. The accuracy of the algorithm is then defined as:

We will implement the analysis code in a different file, analysis.py.

Step 1: Load the final centroids: what happened?

Now we can start the analysis. We have provided the code for you near the bottom of analysis.py: 

if __name__ == "__main__":
    centroids = load_centroids("mnist_final_centroids.csv")
    # Consider exploring the centroids data here
    
    # main_test()
    
    # data, label = read_data("data/mnist.csv") 
    # print(accuracy(data, label, centroids))

First, please take a closer look at this centroids dictionary and/or the images that were generated. Feel free to write some print statements to explore the content (you don't need to show this code when you submit your homework) - how many centroids are there in the dictionary now? In Part A, we initialized the algorithm with 10 randomly chosen positions as the initial centroids. Why are there fewer centroids than 10 now? What do you suspect happened? >This question is just for fun (un-graded), but we want you to at least think about what is happening and give an answer. Leave your answers as comments at the bottom of the file (analysis.py). Please do not stress about these questions! There is no need to do anything for this question other than think about it.

Step 2: Rewrite update_assignment

When we implemented the update_assignment function, it assigned each data point to the centroid it is closest to. This works great for our algorithm, but now we are not only interested in which centroid the data point is assigned to, but also the true label of that data point in order to perform the accuracy analysis. Therefore, we need to update the function to incorporate more parameters and return different values. Implement the following function in analysis.py: 

def update_assignment(list_of_points, labels, centroids_dict):
    """
    Assign all data points to the closest centroids and keep track of their
    labels. The i-th point in "data" corresponds to the i-th label in "labels".

    Arguments:
        list_of_points: a list of lists representing all data points
        
        labels: a list of ints representing all data labels
                labels[i] is the label of the point list_of_points[i]
        centroids_dict: a dictionary representing the centroids where the keys
                        are strings (centroid names) and the values are lists
                        of centroid locations

    Returns: a new dictionary whose keys are the centroids' key names and
    values are a list of labels of the data points that are assigned
            to that centroid.

    Example:
        Code:
            list_of_points = [[1.1, 1, 1, 0.5], [4, 3.14, 2, 1], [0, 0, 0, 0]]  
            labels = [2, 1, 3]  
            centroids_dict = {"centroid1": [1, 1, 1, 1],
                            "centroid2": [2, 2, 2, 2]}
            print(update_assignment(list_of_points, labels, centroids_dict))
        Output:
            {'centroid1': [2, 3], 'centroid2': [1]}
    """

Notice the red parts as the difference between the previous version of the function you wrote and what you need to write now. Instead of nested lists of data points as the values of the dictionary returned, it should now be single lists that contain the labels of the data points, not the actual data points. Feel free to copy your previous implementation in kmeans.py over as a starting point. And just like your old implementation, you should use the get_closest_centroid function when implementing this one.

We have provided testing code for you to verify your implementation. De-comment the call to main_test() near the bottom of analysis.py and then run python analysis.py, which will call that same main_test(). Similar to part 1, you should see 

test_update_assignment passed
if your update_assignment is working. You will see a test fail after that, since your other functions are not ready yet.

Step 3: Calculate the count of the majority label

In the next function, you should take in a single list of labels, and return the count of the majority label defined as above. Implement the following function in analysis.py: 

def majority_count(labels):
    """
    Return the count of the majority labels in the label list

    Arguments:
        labels: a list of labels

    Returns: the count of the majority labels in the list
    """

We have provided testing code for you to verify your implementation. Run python analysis.py again. This time you should see 

test_majority_count passed
if your majority_count is working. You will see a test fail after that, since your last function is not ready yet.

Step 4: Calculate the accuracy of the algorithm

Use the two functions you implemented in the previous parts of Part 2 to calculate the accuracy for every cluster and the whole algorithm, defined as above in the Analyzing the Performance section. Implement the following function in analysis.py: 

def accuracy(list_of_points, labels, centroids_dict):
    """
    Calculate the accuracy of the algorithm. You 
    should use update_assignment and majority_count 
    (that you previously implemented)

    Arguments:
        list_of_points: a list of lists representing all data points
        labels: a list of ints representing all data labels
                labels[i] is the label of the point list_of_points[i]
        centroids_dict: a dictionary representing the centroids where the keys
                        are strings (centroid names) and the values are lists
                        of centroid locations

    Returns: a float representing the accuracy of the algorithm
    """

We have provided testing code for you to verify your implementation. Run python analysis.py again. This time you should see 

test_accuracy passed
if your accuracy function is working. Now you should also see 
all tests passed.

Step 5: Run analysis and think about the results

You have now completed all the parts required to run the analysis. Please de-comment the last few commented lines of code at the bottom of analysis.py and comment out the call to main_test() (and remove your exploration code from Step 1) so you have: 

if __name__ == "__main__":
    centroids = load_centroids("mnist_final_centroids.csv")
    
    # main_test()
    
    data, label = read_data("data/mnist.csv") 
    print(accuracy(data, label, centroids))

And run the program by typing: 

python analysis.py
Note that the file name returned in the output does not necessarily correspond with the label assigned to the digit (ex. centroid0.png is not necessarily an image of '0'). Instead, decide on the label of the image by looking at the returned image itself. What is the output? Is this value surprising? It might be helpful to take another look at the final centroid images from MNIST in the results/MNIST/final folder -- In your opinion, based on these centroids, which digits are easier to be distinguished by the algorithm, and which are harder? If you can't tell from the centroid images, consider printing the accuracy for each label inside of your accuracy function. This question is graded, but don't stress too much about it. Reasonable answers will receive full credit. (ie 2-3 sentences). Leave your answer as comments at the bottom of the file analysis.py. There is no need to do anything for this question other than think about it.

Step 6: Final Submit!

Now you are done!

Be sure to submit both analysis.py and kmeans.py via Gradescope under part 2.

Answer a REQUIRED survey asking how much time you spent and other reflections on this part of the assignment.