HW4 Check-in Due: at 11:59pm on Thursday, Feb 13, 2020. Submit this fairly
long: Gradescope Quiz
Part I Due: at 11:59pm on Tuesday, Feb 18, 2020. Submit via
Gradescope. (REQUIRED Feedback Survey)
Part II Due: at 11:59pm on Monday, Feb 24, 2020. Submit via
Gradescope. (REQUIRED Feedback Survey)
Learning Objectives:
When you sign into Facebook, it suggests friends. In this assignment, you will write a program that reads Facebook data and makes friend recommendations.
Advice from previous students about this assignment: 14wi 15sp
Facebook suggests people you may be (or should be) friends with. Netflix suggests movies you might like. Amazon suggests products to buy. How do they do that? In this assignment, you will learn one simple way to make such suggestions, called collaborative filtering. The actual algorithms used by these companies are closely-guarded trade secrets.
A computer system that makes suggestions is called a recommender system. As background, there are two general approaches: collaborative filtering and content-based filtering.
In this assignment, you will implement a collaborative filtering recommendation system for suggesting friends on Facebook.
A graph or network represents relationships among things. The things are represented as nodes or vertices, and the relationships are represented as edges.
One common use for a graph is to represent travel possibilities, such as on a road map or airline map. The nodes of the graph are cities, and the edges show which cities are directly connected. Then, you can use the graph to plan travel.


Another common use for a graph is to represent friendship among people in a social network. For example, here is the friendship graph for some of the characters of “Romeo and Juliet”:
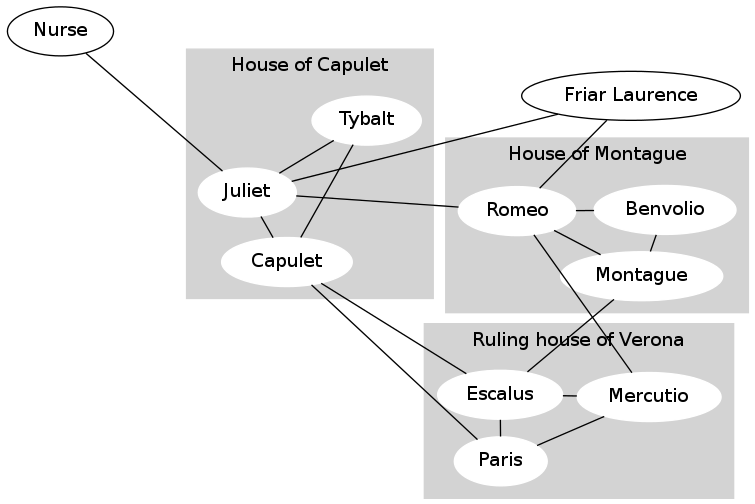
An edge between person A and person B means that A considers B a friend, and also B considers A a friend.
This graph is unable to represent certain information. For example, Count Paris wishes to wed Juliet, but she does not reciprocate his affection. You do not need to worry about this information, because Facebook does not represent this information either. (Some other social networking sites, such as Twitter and Google+, do permit one-way links.)
In the image above, ignore the gray background and the labels for the families ("houses"); those are there just to help you interpret the graph but are not part of the social network itself.
In this assignment you will implement two mechanisms for recommending a new friend in a social network. A simple way to state this question is, “For user X, who is the best person to recommend for them as a friend?”
You will answer a more comprehensive question: “For user X, list some non-friends in order, starting with the best friend recommendation and ending with the worst.” A non-friend is a user who is not X and is not a current friend of X. Depending on the recommendation algorithm, the list may include all non-friends of X or some of them.
For example, for Mercutio the list might be:
Capulet
Montague
Benvolio
Friar Laurence
Juliet
Further note that the recommendations might not be symmetric: the best friend recommendation for Montague might be Mercutio, but the best friend recommendation for Mercutio might be Capulet.
Your task will be to write code that, given a user U in the social network, produces friend recommendations for U, in order from best to worst. You will do this by assigning each potential friend a number called a score, where higher scores indicate a better match. Then you can sort your list according to the score. Given user X, if two people Y and Z would be equally good as new friends for X (they have the same score), then they should be listed in alphabetical order (for names as in Part I) or numerical order (for numerical user IDs as in Part II).
First, download and unzip the file homework4.zip.
Here is a smaller facebook file that you can use for testing: facebook-links-small.txt. Sample output for this file is here. (Both files are also included in the .zip file linked above.) You can cut and paste the output from your program and the file above into the Diff Checker tool to comfirm you are getting the correct output. Feel free to make even smaller files of your own for testing purposes!
By the end of the assignment, running social_network.py must produce output of the exact form:
Problem 4: Unchanged Recommendations: ['____', '____', ...] Changed Recommendations: ['____', '____', ...] Problem 6: ... ____ (by number_of_common_friends): [____, ____, ____] ____ (by number_of_common_friends): [____, ____] ____ (by number_of_common_friends): [____, ____, ____, ____, ____] ... Problem 7: ... ____ (by influence): [____, ____, ____, ____, ____, ____, ____, ____, ____] ____ (by influence): [____] ____ (by influence): [____, ____, ____, ____, ____, ____, ____, ____, ____, ____] ... Problem 8: Same: ___ Different: ___
Where ... indicates that there may be more of these lines, and where all of the ____ are replaced by values that you will calculate. For problems 6 and 7 each line may have a different number of values than what is shown above, and you will be printing more than 3 lines of output - these are just examples. Of course, the exact values in each category will vary depending on the input data that you are using. We expect the formatting of your program output to exactly match this.
If you are using Andaconda Python and the cse160 environment you should be ready to go!
If you get the error:
ImportError: No module named networkx
then you may not be running the correct version of Python. Other distributions of Python do not necessarily include the NetworkX library, which means they cannot be used for this assignment.
The NetworkX library represents a graph in Python. Make sure you understand the examples from the lecture slides on graphs. Skim through the NetworkX tutorial, up to and including the What to use as nodes and edges section. Be sure you understand add_edge(), add_node(), edges(), nodes(), and neighbors(). The tutorial discusses more operations than you need to know. Do not worry if you do not understand all the details in the tutorial (e.g. you can ignore nbunches and ebunches). You may also want to browse the Drawing graphs section.
As seen on the Lecture Slides on Graphs, to use the networkx library in a program, write import networkx or import networkx as nx near the top of your program. The latter has already been done for you in the supplied social_network.py, so you can use shorter commands like nx.draw_networkx(...) instead of the (slightly longer) networkx.draw_networkx(...). There is nothing to turn in for this step.
It is always a good idea to test your code on a dataset that is small enough for you to manually compute the results. You will create two such datasets for testing.
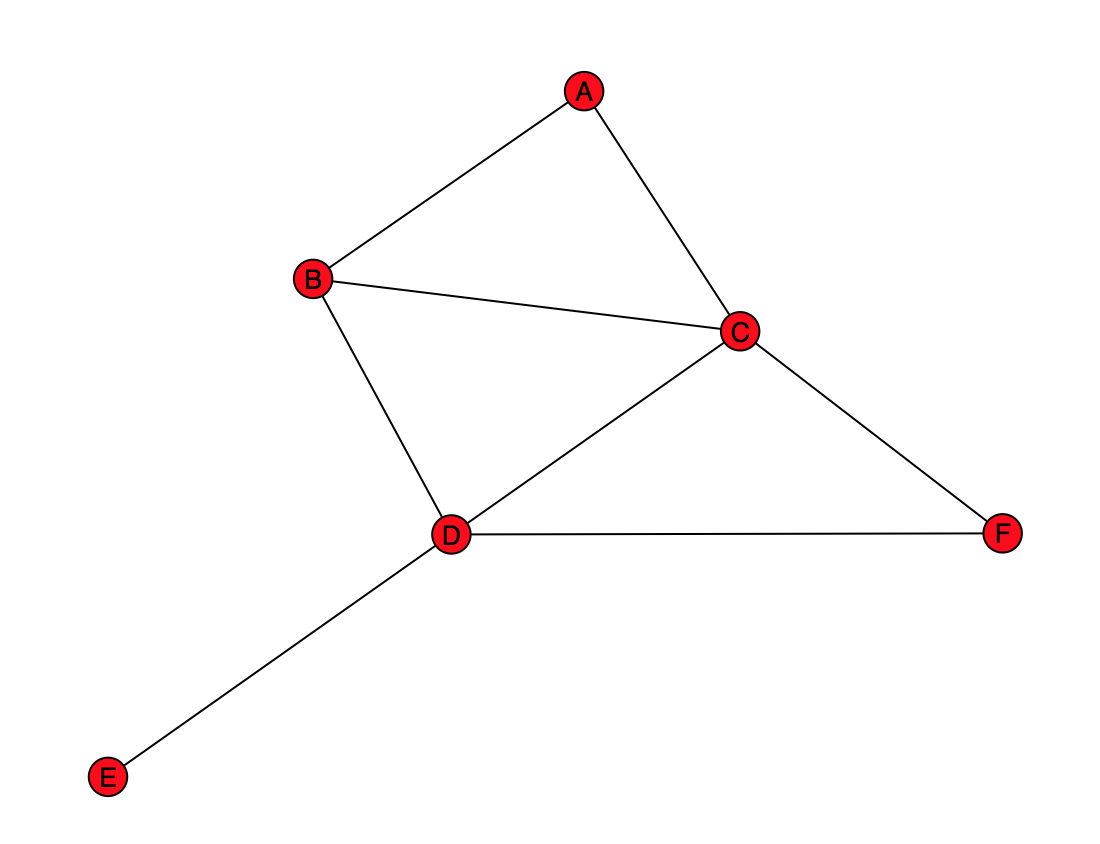
Create the above graph, and store it in a variable named practice_graph. Note that there are letters inside each node (these may not show up in a printout of the assignment.) Use the Graph class as demonstrated in lecture (not DiGraph, MultiGraph, or MultiDiGraph).
To help you verify that your graph is correct, the provided code draws the graph to a window. The graph may be hidden behind other windows, so look for it! Compare your graph to the figure above. The nodes may appear in different locations; that's fine so long as the same nodes exist and they are connected in the same way by the edges. Note that if you redraw this graph the nodes may be plotted using a different layout each time - this is also fine!
Note that your program will pause until you close the window that contains the graph drawing.
When you are happy with your graph, comment out the call to draw_practice_graph() (not the definition of the draw_practice_graph function). The reason is so that you don't have to close the window every time you run your program.
Note that you may find several assertions further down in the program failing at this point. This is to be expected since you have not implemented those parts of the program yet! In fact this will continue to happen as you progress through the problems. Success usually means you are no longer failing the same assertion, but that instead a different assertion is failing further down in the program.
Create a graph named rj corresponding to the Romeo and Juliet graph above (ignoring the shaded family/house information).
To help you verify that your graph is correct, the provided code draws the graph to a window and to a file romeo-and-juliet.pdf. Compare your graph to the Romeo and Juliet graph above. The nodes may appear in different locations; that's fine so long as the same nodes exist and they are connected in the same way by the edges. (We added assert statements to check this for you.)
When you are happy with your graph and the romeo-and-juliet.pdf file, comment out the call to draw_rj() (not the definition of the draw_rj function). The reason is so that you don't have to close the window every time you run your program.
If non-friend Y is your friend's friend, then maybe Y should be your friend too. If person Y is the friend of many of your friends, then Y is an even better recommendation. The best friend recommendation is the person with whom you have the largest number of mutual friends. You will implement this heuristic.
As a concrete example, consider "A" in practice_graph. Say we are interested in giving "A" recommendations of people that they might want to be friends with. By this algorithm, the number of friends you have in common with someone is a measure of how likely it is that they would be a good friend recommendation for you. Thus the more friends someone has in common with you, the better their "friendship score" is. We will actually use the number of friends in common as the friendship score itself. Thus we want to find out who has the most friends in common with "A".
A has one friend in common with B (namely, C), but A and B are already friends, so we would not recommend B.
A has one friend in common with C (namely, B), but A and C are already friends, so we would not recommend C.
A has two friends in common with D (namely, B and C).
A has no friends in common with E, so we would not recommend E.
A has one friend in common with F (namely, C).
D is the best recommendation for A, F is the second best recommendation. We would not recommend B or C because A is already friends with them. We also would not recommend E because A has no friends in common with E.
Similarly, consider Mercutio in the Romeo and Juliet graph.
Mercutio has two friends in common with Capulet (Escalus and Paris).
Mercutio has two friends in common with Montague (Escalus and Romeo).
Mercutio has one friend in common with Friar Laurence (Romeo).
Mercutio has one friend in common with Benvolio (Romeo).
Mercutio has one friend in common with Juliet (Romeo).
Mercutio has no friends in common with the Nurse, so we would not recommend the Nurse.
Mercutio has no friends in common with Tybalt, so we would not recommend Tybalt.
Therefore, Capulet and Montague are the best friend recommendations for Mercutio. (Note that we are not listing Paris, Escalus or Romeo who are already friends of Mercutio.) So our algorithm would want to return to Mercutio this list ordered from best recommendation to worst. In the case of ties in friendship score (such as between Capulet and Montague, or between Benvolio, Friar Laurence, Juliet), we list people alphabetically. Thus we would return:
['Capulet', 'Montague', 'Benvolio', 'Friar Laurence', 'Juliet']Now let's think about how we might create this list. Obviously we will need to calculate these "friendship scores" for some set of people in the graph. By this "number of common friends" metric, for a given person, we really only care about calculating such scores for people that are "friends of our current friends" who are not yet our friends. (There could be many people in a large graph, so we do not want to simply calculate friendship scores for every person in the graph as many of those scores are likely to be zero.) So it would be useful to be able to calculate the set of "friends of friends" for a given user. For each of those friends-of-friends we will want to be able to calculate the set of friends that they have in common with the user. If we want to return to the user a ranked list of recommendations from best recommendation to worst, then it would be useful to have a data structure to keep track of the mapping of "friend of friend" to friendship score. Finally, given this mapping of people to friendship scores, we will want to sort the potential friends from best to worst before presenting it to the user. (Hint: Remember that a dictionary is often called a "map".)
For this problem, you need to write the following 5 functions, whose documentation strings appear in the template file social_network.py that you were provided.
The template file defines a helper function, friends(graph, user), that you may find useful.
The template file also contains assert statements to help you test your code. We strongly encourage you to write additional tests as well, in order to verify that your code is correct. You may also find the assertions useful for clarifying what the function is supposed to return. Remember an assertion states something that is supposed to be true. So when passed the parameters listed in the assertion, we expect your function to return the values listed to the right of the ==.
For all of these functions, we strongly suggest (as do students who completed a similar assignment in previosu quarters - based on their reflection statements) that you start trying to write them on paper first. You should write at least an outline on paper, but it is good practice to write a draft of the code on paper too. This outline is probably a good starting point for the comments you should have inside of the functions.
Hint: Remember that when Python tests sets or dictionaries for equality, it ignores the order of elements. A consequence of this is that two sets can print differently but be equal because they represent the same set, and likewise for dictionaries. For example, this Python expression evaluates to True:
{ 'Capulet', 'Escalus', 'Montague' } == { 'Montague', 'Capulet', 'Escalus' }
Hint: Throughout this assignment, you are permitted, but not required, to define additional functions beyond the required ones.
Hint: Throughout this assignment, use good variable naming! Names like friends_list or friends_set for example may help you remember what *type* a particular variable is referring to (e.g. a list or a set).
Hints for friends_of_friends and common_friends: When defining these two functions, you should not use any data structures other than sets. If you find yourself using even one list or dictionary, then you are doing the problem wrong. The reason to use sets is that the code is much shorter and simpler. In fact, a solution to friends_of_friends can be as short as 4 lines long, and a solution to common_friends could be only 1 line long. Longer solutions are possible and can also be good style, but the point is that these are small, simple functions. The other functions you will define are little, if any, longer.
Hints for number_map_to_sorted_list:
We will now give a different algorithm for computing a friendship score.
Consider the following hypothetical situation.
Two of your friends are J.D. Salinger and Tim Kinsella.
J.D. Salinger has only two friends (you and one other person).
Tim Kinsella has 7 billion friends.
J.D. and Tim have no friends in common (besides you).
Since J.D. is highly selective in terms of friendship, and is a friend of yours, you are likely to have a lot in common with J.D.'s other friend. On the other hand, Tim is indiscriminate and there is little reason to believe that you should be friendly with any particular one of Tim's other friends.
Incorporate the above idea into your friend recommendation algorithm.
Here is the concrete way that you will do so. We call the technique
“influence scoring”.
Suppose that user1 and user2 have three friends in common: f1, f2, and f3.
In Problem 2, the score for user2 as a friend of user1 is 1+1+1: each
common friend contributes 1 to the score.
In this problem, the score for user2 as a friend of user1 is
1/numfriends(f1) + 1/numfriends(f2) + 1/numfriends(f3), where numfriends(f)
is the number of friends that f has. In other words, each friend F of user1
has a total influence score of 1 to contribute, and divides it equally among all of
F's friends.
In the example above, J.D. Salinger's other friend would have a score of 1/2, and each of Tim Kinsella's friends would have a score of 1/7000000000.
We recommend that you calculate by hand what the friendship scores would be for each of the friend recommendations that would be returned to Mercutio using this same metric. To see what the right answer should be, take a look at the assert statement for the influence_map function in the file social_network.py.
**** An example of recommend by influence.
The social_network.py file gives two functions (influence_map and recommend_by_influence) that you should implement. You may find that their implementations are quite similar to code that you have already written in Problem 2; that is OK. The file also gives one test case for each of the two functions.
Do not change the code that you wrote for Problem 2. However, you will find that you can call many of the functions you wrote for Problem 2. You can solve the problem with just the two new functions (influence_map and recommend_by_influence), plus re-using some unchanged functions from Problem 2.
Does the change of recommendation algorithm make any difference? Maybe not: you can see by looking at the assert statements in social_network.py that Mercutio should get the same friend recommendations with both recommendation approaches. Does everyone get identical results with the two recommendation approaches?
Write code to print a list of people for whom the two approaches make the same recommendations, then print a list of people for whom the two approaches make different recommendations. Each list should be sorted in alphabetical order. You do not need to write a function that does this, writing code at the global level is fine.
Print out the results for the Romeo and Juliet graph. The format of this problem's printed output is given above, near the beginning of the assignment.
Hint: In the Romeo and Juliet graph there are 5 people for whom the recommendations are the same, and 6 people for whom the recommendations are different.
You are almost done with Part I!
Answer this REQUIRED Feedback survey asking how much time you spent on this part of the assignment and other reflections on this part of the assignment.
Submit the following files via Gradescope.Now you are done with Part I! On to Part II!
For the code in Part II, it is fine if you do not write any new functions. It is fine if you do write new functions, but you will not be graded down if you do not.
Create a graph named facebook from the Facebook data in file facebook-links.txt. As above, use the Graph class.
Here is a smaller facebook file that you can use for testing: facebook-links-small.txt. Sample output for this file is here. (Both files are also included in the .zip file linked above.) You can use the Diff Checker tool to compare your ouput to the sample output provided above. Feel free to make even smaller files of your own for testing purposes!
You do not need to read in the file name from the command line as we did in hw2 and hw3. Instead you can just assume that the file facebook-links.txt will be present in the same directory as social_network.py and use the filename as "facebook-links.txt" in your program as needed. We recommend that you run the program from the command line as you have before, although hitting the green button in VSCode should also work.
Looking at the assert statements in social_network.py notice that the number of nodes in your facebook graph should be 63731.
The facebook-links.txt file in your homework4 directory is courtesy of the Max Planck Institute for Software Systems. Here is a slightly clarified version of the documentation for this file:
File facebook-links.txt contains a list of all of the user-to-user links from the Facebook New Orleans networks. These links are undirected on Facebook.
Format: Each line contains two numeric user identifiers, meaning the second user appeared in the first user's friend list, and the first user appeared in the second user's friend list. Finally, the third column is a UNIX timestamp with the time of link establishment (if it could be determined, otherwise it is '\N').
A Unix timestamp is the number of seconds since January 1, 1970. You may ignore timestamps in this assignment. (Facebook does use the recency of your activity to help it in making recommendations.)
A snippet of the file appears below:
35467 17494 1197992662 35467 4190 \N 35467 18822 1209937599 37188 7741 1219156787 37188 8561 1199853037
When reading in this data you should be sure to convert the numeric user identifiers into ints. Storing them as ints will make your life easier and is the output format that we require for printing (Do NOT print a user ID as '19611' instead print as 19611.) This means your code should work whether nodes are named with strings (as we did with the practice graphs) or ints (as we are doing with the facebook data). In NetworkX nodes can be strings or integers.
Hint: You may find it useful to refer to the slides about File I/O.
Hint: Don't be alarmed if reading the Facebook data takes a little while. The file is large, and it may take up to a minute for your program to read it. However, do not try to draw the Facebook graph. This may cause your computer to hang, and even if it were successful, you would not learn much from a tangled mess of 817,090 edges.
For every Facebook user with a user id that is a multiple of 1000, print a list containing the first 10 friend recommendations, as determined by "number of common friends" friendship score. If there are fewer than 10 recommendations, print all the recommendations.
You can review more details about the format for the printed output near the beginning of the assignment. This is a sample of part of what you would expect for your output (you should be printing more lines than this, but they should be listed in ascending order of userID as shown below):
... 28000 (by number_of_common_friends): [23, 1445, 4610, 7996, 10397, 11213, 56, 85, 471, 522] 29000 (by number_of_common_friends): [28606] 30000 (by number_of_common_friends): [862, 869, 919, 941, 3154, 8180, 8269, 8614, 14473, 14495] ...
Hint: List slices may be useful for Problem 6 and 7.
For every Facebook user with a user id that is a multiple of 1000, print a list containing the first 10 friend recommendations, as determined by the "influence" friendship score. If there are fewer than 10 recommendations, print all the recommendations.
You can review more details about the format for the printed output near the beginning of the assignment. This is a sample of part of what you would expect for your output (you should be printing more lines than this, but they should be listed in ascending order of userID as shown below):
... 28000 (by influence): [7033, 17125, 15462, 33049, 51105, 16424, 23, 7996, 725, 1539] 29000 (by influence): [28606] 30000 (by influence): [862, 869, 919, 941, 3154, 8269, 14473, 14495, 17951, 19611] ...
Considering only those 63 Facebook users with an id that is a multiple of 1000, compute and print the number of Facebook users who have the same first 10 friend recommendations under both recommendation systems, and the number of Facebook users who have different first 10 friend recommendations under the two recommendation systems. For example, in the data above, user 29000 has the same first ten recommendations under both recommendation systems, while user 28000 and user 30000 both have different recommendations under the two recommendation systems. This program may take some time to compute (possibly a minute or so).
The format of this problem's printed output is given above, near the beginning of the assignment.
You are almost done!
At the bottom of your social_network.py file, in the “Collaboration” part, state which students or other people (besides the course staff) helped you with the assignment, or that no one did.
Submit social_network.py via Gradescope.
Answer this REQUIRED Feedback Survey asking how much time you spent and other reflections on Part II of the assignment.
Now you are done!