we define the distance between points a and b as:
Part I Due: at 11:59pm on Monday, Nov 30, 2020. Submit via Gradescope.
(REQUIRED Feedback
Survey)
Part II Due: at 11:59pm on Friday, December 4, 2020. Submit via Gradescope.
(REQUIRED Feedback
Survey)
In Homework 5, we will implement a commonly-used algorithm -- K-means clustering. K-means is a popular machine learning and data mining algorithm that discovers potential clusters within a dataset. Finding these clusters in a dataset can often reveal interesting and meaningful structures underlying the distribution of data. K-means clustering has been applied to many problems in science and still remains popular today for its simplicity and effectiveness. Here are a few examples of recently published papers using K-means:
Hopefully, these examples motivate you to try this homework out! You will very likely be able to apply this computational tool to some problems relevant to you! Though appearing in many advanced fields of science, the essence of K-means is not difficult to understand. We will break down the name and explain the algorithm now.
We will assume we have a dataset of m data points where each data point is n-dimensional. For example, we could have 100 points on a two dimensional plane, then m = 100 and n = 2.
Given two n-dimensional points a and b where:
we define the distance between points a and b as:
This is commonly known as the Euclidean distance. For example, the
Euclidean distance between the three-dimensional points x1 and x2
(displayed as Python lists) is:
x1 = [-2, -1, -4], x2 = [10, -5, 5]
Here is another example of two four-dimensional points:
x1 = [0, 0, 1, 1], x2 = [1, 1, 0, 0]
A centroid can be seen as the “center of mass” of a group of points.
In K-means, we assume that the centroid of a cluster is the mean
of all the points in that cluster. The mean data point consists
of the mean of the components on each dimension. Say, for three
n-dimensional points a, b, and c, we have the mean as:
For example, if a cluster contains three 2D points
(displayed as Python lists) as below:
x1 = [1, 2], x2 = [3, 4], x3 = [5, 6]
The centroid for this cluster is defined as:
C = [(1 + 3 + 5)/3, (2 + 4 + 6)/3] = [3, 4]
Our ultimate goal is to partition the data points into K clusters.
How do we know which data point belongs to which cluster?
It is actually extremely hard to find the “optimal” answer for this,
but K-means takes a simple, heuristic approach - we simply assign
a data point to the centroid whose distance to the data point is
the smallest (the “closest centroid” to this data point)!
Let’s assume we already have K centroids, initialized randomly.
Now, if our randomly initialized centroids were already in good
locations, we would have been done! However, it is most likely that
the initial centroid locations do not reflect any information about
the data (since they were just random). To update the centroid locations
to something that makes more sense we use an iterative approach:
One last question you may have is, when do we stop repeating these two steps?
I.e., what does it mean for the algorithm to have converged?
We say the algorithm has converged if the locations of all centroids
did not change much between two iterations.
Take this example of two centroids of 2-dimensional points.
If at the previous iteration, we have the two centroid locations as:
c1 = [0.45132, -0.99134], c2 = [-0.34135, -2.3525]
And at the next iteration the centroids are updated to:
c1 = [1.43332, -1.9334], c2 = [-1.78782, -2.3523]
Then we say the algorithm has NOT converged, since the location
of the two centroids are very different between iterations.
However, if the new locations of the centroids are instead:
c1 = [0.45132, -0.99134], c2 = [-0.34135, -2.3524]
Then we say the algorithm HAS converged, since the locations
of the two centroids are very similar between iterations
(Typically, “very similar” means for every dimension of two points
a and b, their difference (|a - b|) is smaller than some constant
(1e-5 is a common choice)).
In summary, the K-means algorithm (in pseudo code) is described as follows:
data = Load Data
centroids = Randomly Created K Centroids
while centroids not converged:
for each data point:
assign data point to the closest centroid
for each centroid:
set new centroid location to be the mean of
all points in this cluster
The following gif visualizes this process, and will be what you accomplish in Part 1! The initial frame (step0) is the initialization: two randomly chosen centroids are drawn as an X in blue (centroid 0) and red (centroid 1). Then in the following steps (step1 through step6):
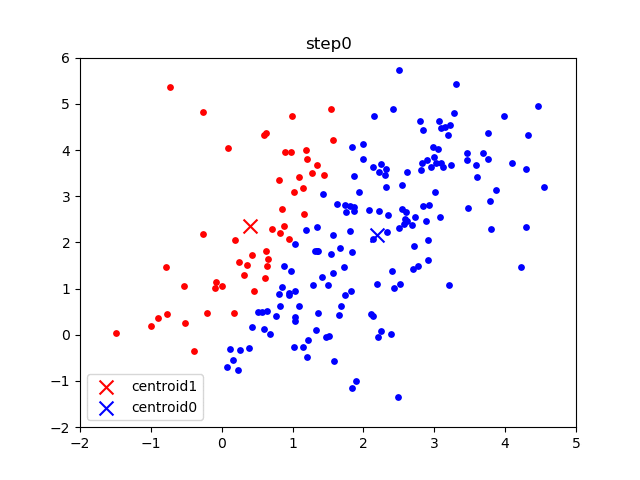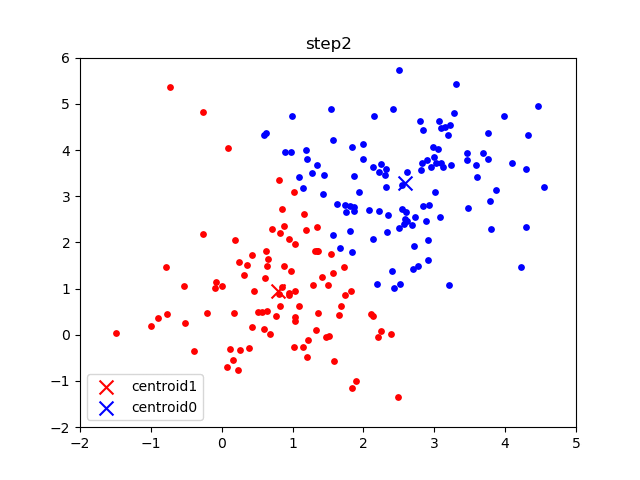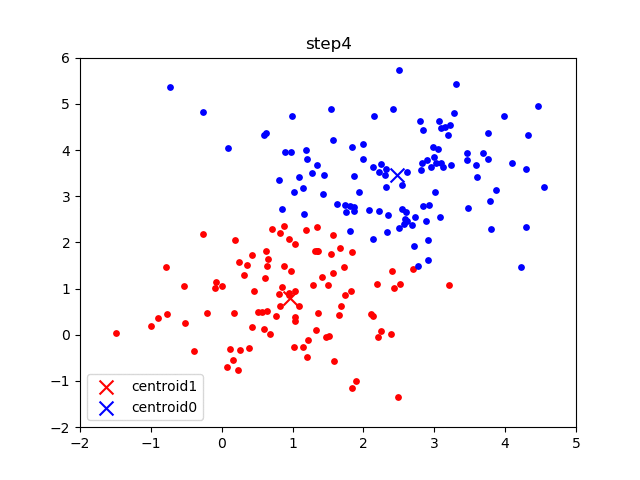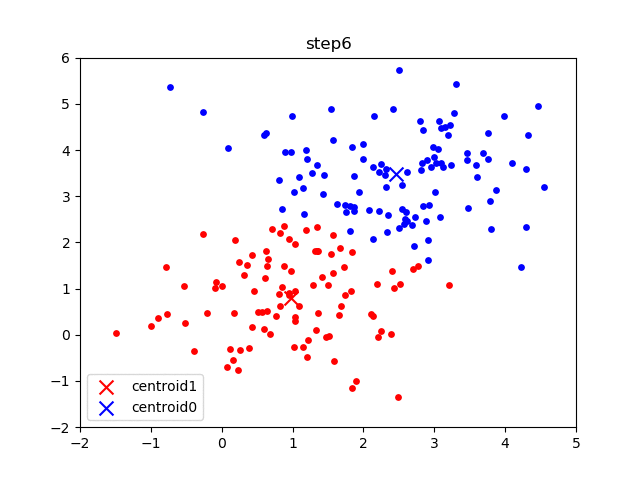
In the following parts of this homework, you will implement this algorithm and apply it to (1) 2D points shown in the gif above; (2) a small subset of the MNIST hand-written digit dataset.
Please download homework5.zip and unzip the file to get started. You should see the following file structure in the homework5 folder:
homework5 ├── __init__.py ├── analysis.py [Your code for Part 2B] ├── data [data to run the programs with] │ ├── 2d_init_centroids.csv │ ├── data_2d.csv │ ├── mnist.csv │ └── mnist_init_centroids.csv ├── kmeans.py [Your code for Part 1 & Part 2A] ├── results [Where your result figures will be saved] │ ├── 2D │ └── MNIST │ ├── final │ └── init ├── kmeans_tests.py [Testing code: Don’t edit] ├── analysis_tests.py [Testing code: Don’t edit] └── utils.py [Helper code: Don’t edit]
The red highlighted part is where you will work on your code. We have provided utils.py which contains helper code to help you complete the assignment, as well as kmeans_tests.py and analysis_tests.py which contain testing code to verify your implementations. Do not change anything in these three files!
You will be given the following data structures for K-means clustering:
Implement the following function in kmeans.py:
def euclidean_distance(data1, data2):
"""Calculate the Euclidean distance between two data points.
Arguments:
data1: a list of floats representing a data point
data2: a list of floats representing a data point
Returns: the Euclidean distance between two data points
"""
In the code we have provided you for this (and all functions
you need to implement), the body of the function is empty
except for a single statement: pass. This is a
Python statement that does nothing, but can be used in
situations where you need an instruction to be there
but you don’t want it to do anything. In previous homeworks we
had something like:
print("Remove this statement when you have implemented this function.").
It is more common to see something like a single pass statement
as a placeholder. Please REMOVE the pass statement when you have
finished implementing the function.
We have provided testing code for you to verify your
implementation. Uncomment this line:
test_eucliean_distance()at the bottom of kmeans_tests.py and run python kmeans_tests.py in a terminal window to verify your implementation. If you passed our tests, you should see:
test_eucliean_distance passed.
Implement the following function in kmeans.py:
def assign_data(data_point, centroids):
"""Assign a single data point to the closest centroid. You should use
the euclidean_distance function (that you previously implemented).
Arguments:
data_point: a list of floats representing a data point
centroids: a dictionary representing the centroids where the keys are
strings (centroid names) and the values are lists of
centroid locations
Returns: a string as the key name of the closest centroid to the data point
"""
We have provided testing code for you to verify your implementation. Uncomment this line:
test_assign_data()at the bottom of kmeans_tests.py and run python kmeans_tests.py in a terminal window to verify your implementation.
Implement the following function in kmeans.py:
def update_assignment(data, centroids):
"""
Assign all data points to the closest centroids. You should use
the assign_data function (that you previously implemented).
Arguments:
data: a list of lists representing all data points
centroids: a dictionary representing the centroids where the keys are
strings (centroid names) and the values are lists of
centroid locations
Returns: a new dictionary whose keys are the centroids' key names and
values are lists of points that belong to the centroid. If a
given centroid does not have any data points closest to it,
do not include the centroid in the returned dictionary.
"""
Notice that your algorithm should run regardless of if any
centroid becomes empty, i.e. there are no points that are the
closest to a centroid. In that case you should not include
that centroid in the dictionary you return.
We have provided testing code for you to verify your implementation.
Uncomment this line:
test_update_assignment()at the bottom of kmeans_tests.py and run python kmeans_tests.py in a terminal window to verify your implementation.
Implement the following function in kmeans.py:
def mean_of_points(data):
"""Calculate the mean of a given group of data points. You should NOT
hard-code the dimensionality of the data points.
Arguments:
data: a list of lists representing a group of data points
Returns: a list of floats as the mean of the given data points
"""
We have provided testing code for you to verify your implementation. Uncomment this line:
test_mean_of_points()at the bottom of kmeans_tests.py and run python kmeans_tests.py in a terminal window to verify your implementation.
def update_centroids(assignment_dict):
"""
Update centroid locations as the mean of all data points that belong
to the cluster. You should use the mean_of_points function (that you
previously implemented).
Arguments:
assignment_dict: the dictionary returned by update_assignment function
Returns: A new dictionary representing the updated centroids
"""
Notice that you should not hard-code the dimensionality of data - your code needs to run regardless of the dimension of data! We have provided testing code for you to verify your implementation. Uncomment this line:
test_update_centroids()at the bottom of kmeans_tests.py and run python kmeans_tests.py in a terminal window to verify your implementation.
python kmeans_tests.pyin the terminal window. You should see:
All tests passed.
You have now completed all parts needed to run main()! Now, let’s verify your implementation by running the algorithm on 2D points. At the bottom of kmeans.py, make sure you have:
if __name__ == '__main__':
data, label = read_data("data/data_2d.csv")
init_c = load_centroids("data/2d_init_centroids.csv")
final_c = main_2d(data, init_c)
write_centroids_tofile("2d_final_centroids.csv", final_c)
This says you are loading the 2D data points and the initial centroids we provided in from .csv files, and calling the main function. Run the program by typing this:
python kmeans.pyin the terminal window. If you are successful, you should see:
K-means converged after 7 steps.as the output of the program. In addition, there should be 7 plots generated, in the results/2D/ folder. If you examine these 7 plots, they should be identical to the steps shown in the the gif above.
Now that you have successfully run K-means clustering on
2-dimensional data points with 2 centroids, we will use
your code to do clustering of 784-dimensional data points
with 10 centroids. Don’t worry, you won’t need to change
any of the code that you wrote!
We will apply the algorithm to a real world data set known
as the Modified National Institute of Standards and Technology
database (MNIST). It is a dataset that consists of images of
hand-written digits. Here are nine examples images from the
MNIST data set (we are using a very small subset of all MNIST images):

Each of these images is 28 pixels by 28 pixels, for a total of 784 pixels.
(As in HW3, pixels have values between 0 and 255 (0=black, 255=white),
although we don’t need to know this for K-means.) Each image can be
thought of as a 784-dimensional data point, represented as a list
containing 784 numbers. For the images shown above, many of the
numbers would be zero since the image is mostly black. So the nine
sample images above are actually nine sample data points!
We will see how applying K-means to these digit images helps us
discover clusters of images which contain mostly one kind of digit!
To load the MNIST dataset instead of the 2D points, change the code
at the bottom of the file to the following (the red text shows the
changes that should be made):
data, label = read_data("data/mnist.csv")
init_c = load_centroids("data/mnist_init_centroids.csv")
final_c = main_mnist(data, init_c)
write_centroids_tofile("mnist_final_centroids.csv", final_c)
You should leave the rest of your code intact, and it should run with the new data without errors! Run this command again (it may take a minute to run on this data set!):
python kmeans.py
You should see the following output:
K-means converged after 18 steps.Meanwhile, in the results/MNIST folder, the init and final folders should be filled with the centroids plotted as images. Remember that centroids are basically a data point that represents the average of all the data points (images) that are assigned to it.

How do we evaluate the performance of our algorithm? The images in
the MNIST data set have been labelled with the digit they actually
represent. (You can see this label as the digit in the first column
on each row in the file mnist.csv. Each row of that file represents
one data point (image).) So, one way to evaluate our algorithm would
be to examine the accuracy of the classification of the images from
MNIST. For example, how many of the images known to be (labelled as)
the digit 4 ended up in the centroid we think of as representing the
digit 4?
First, let’s define the “classifications” of our data points provided
by K-means. We take a majority-takes-all approach: we assign each
cluster a label as the majority labels of all data points in this
cluster. For example, say we have data points with these labels
assigned to cluster1:
2, 2, 2, 2, 2, 2, 8, 6, 2, 2, 6, 8, 8, 2, 2Since there are 10 2’s, 3 8’s, and 2 6’s, we say the label of cluster 1 is 2 since it’s the majority label.
In Part A, you ran the algorithm on MNIST data, and wrote the final centroids to a file. The first step in our analysis is to load the results. We have provided the code for you at the bottom of analysis.py:
if __name__ == '__main__':
centroids = load_centroids("mnist_final_centroids.csv")
However, please take a closer look at this centroids dictionary and/or the images that were generated. Feel free to write some print statements to explore the content (you don’t need to show this code when you submit your homework) - how many centroids are there in the dictionary now? In Part A, we initialized the algorithm with 10 randomly chosen positions as the initial centroids. Why are there fewer centroids than 10 now? What do you suspect happened? This question is just for fun (un-graded), but we want you to at least think about what is happening and give an answer. Leave your answers as comments at the bottom of the file (analysis.py). Please do not stress about this question!
When we implemented the update_assignment function, it assigned each data point to the centroid it is closest to. This works great for our algorithm, but now we are not only interested in which centroid the data point is assigned to, but also the true label of that data point in order to perform the accuracy analysis. Therefore, we need to update the function to incorporate more parameters and return different values. Implement the following function in analysis.py:
def update_assignment(data, labels, centroids): """Assign all data points to the closest centroids and keep track of their labels. The i-th point in "data" corresponds to the i-th label in "labels". Arguments: data: a list of lists representing all data points labels: a list of ints representing all data labels centroids: the centroid dictionary Returns: a new dictionary whose keys are the centroids' key names and values are a list of the labels of the data points that are assigned to that centroid. """
Notice the red parts as the difference between the previous
version of the function you wrote and what you need to write now.
Instead of nested lists of data points as the values of the
dictionary returned, it should now be single lists that contain
the labels of the data points, not the actual data
points. Feel free to copy your previous implementation in
kmeans.py over as a starting point. And just like your
old implementation, you should use the assign_data
function when implementing this one.
We have provided testing code for you to verify your implementation.
Uncomment this line:
test_update_assignment()at the bottom of analysis_tests.py and run python analysis_tests.py to verify your implementation.
In the next function, you should take in a single list of labels, and return the count of the majority label defined as above. Implement the following function in analysis.py:
def majority_count(labels):
"""
Return the count of the majority labels in the label list
Arguments:
labels: a list of labels
Returns: the count of the majority labels in the list
"""
We have provided testing code for you to verify your implementation. Uncomment this line:
test_majority_count()at the bottom of analysis_tests.py and run python analysis_tests.py to verify your implementation.
Use the two functions you implemented to calculate the accuracy for every cluster and the whole algorithm, defined as above. Implement the following function in analysis.py:
def accuracy(data, labels, centroids):
"""
Calculate the accuracy of the algorithm. You
should use update_assignment and majority_count
(that you previously implemented)
Arguments:
data: a list of lists representing all data points
labels: a list of ints representing all data labels
centroids: the centroid dictionary
Returns: a float representing the accuracy of the algorithm
"""
We have provided testing code for you to verify your implementation. Uncomment this line:
test_accuracy()at the bottom of analysis_tests.py and run python analysis_tests.py to verify your implementation.
You have now completed all the parts required to run the analysis. Please add a few lines at the bottom of analysis.py (and remove your exploration code from Step 1) so you have:
if __name__ == '__main__':
centroids = load_centroids("mnist_final_centroids.csv")
data, label = read_data("data/mnist.csv")
print(accuracy(data, label, centroids))
And run the program by typing:
python analysis.pyWhat is the output? Is this value surprising? It might be helpful to take another look at the final centroid images from MNIST in the results/MNIST/final folder -- In your opinion, based on these centroids, which digits are easier to be distinguished by the algorithm, and which are harder? This question is graded, but don’t stress too much about it. Reasonable answers will receive full credit. Leave your answer as comments at the bottom of the file analysis.py. Now you are done!