Part 0: Due: Tuesday, Feb 9th at 11:00 PM. Submit this fairly long:
catalyst webQuiz.
Part I: (Problems 0-3) Due: Friday, Feb 12th at 11:00 PM.
Submit your work via this:
turnin page. (survey)
Part II: (Problems 4-7) Due: Friday, Feb 19th at 11:00 PM.Submit your work via this: turnin page.
(survey)
There is one file to turn in: election.py.
Advice from previous students about this assignment: 14wi 15sp

Learning Objectives:
Contents:
In the past, the outcome of political campaigns was predicted by political analysts and pundits, using a combination of their experience, intuition, and personal biases and preferences. In recent decades there has been a shift to a more scientific approach, in which election results are predicted statistically using a poll. A small random sample of voters is asked how they will vote, and from that the result of the entire election is extrapolated.
The 2012 presidential election was a watershed in the fight between pundits and statisticians. The rivalry became front-page news, with many pundits loudly proclaiming that the statisticians would be humiliated on the day of the actual election, November 6. In fact, the opposite happened: statistician Nate Silver (of the website FiveThirtyEight) correctly predicted the outcome in every state, whereas pundits' predictions varied significantly. Literally dozens of prominent political analysts had predicted a Romney win. Other pundits said the election was “too close to call”, though Silver and other statisticians had been predicting an Obama win for months. These results changed the way many Americans view political commentators, revealing them as entertainers but not as reliable sources of information.
How did Nate Silver do it? In this assignment, you will find out, and you will replicate his results by using polling data to predict the outcome of the 2012 US presidential election.
An election poll is a survey that asks a small sample of voters how they plan to vote. If the sample of voters is representative of the voting population at large, then the poll predicts the result of the entire election. In practice, a poll's prediction must be taken with a grain of salt, because the sample is only approximately representative of the voting population. (See below for an explanation of why.)
For example, in late October 2012, the Gallup poll consistently gave Romney a 6-percentage-point lead in the popular vote, but in the actual election Obama won the popular vote by 2.6 percentage points. On the other hand, the RAND Corporation poll was biased toward the Democrats and tended to overstate Obama's lead by 1.5 percentage points. How can you decide which polls to rely upon? Depending on which poll you trust, you might make a very different prediction.
One approach is to average together multiple polls. This is better than trusting any one of them, but it is still rather crude. What if most of them are biased? That was the case for the 23 organizations that conducted at least 5 polls in the last 21 days of the 2012 Presidential campaign: 19 of the 23 organizations gave a result that favored Republicans more than the actual election results did. Yet, Nate Silver's prediction made use of polls but was very close to correct, and showed no bias toward either party.
Silver's approach is very sophisticated, but its key idea is to combine different polls using a weighted average. In a normal average, each data point contributes equally to the result. In a weighted average, some data points contribute more than others. Silver examined how well each polling organization had predicted previous elections, and then weighted their polls according to their accuracy: more biased pollsters had less effect on his weighted average.
The general structure of FiveThirtyEight's algorithm is:
The algorithm is described in more detail at the FiveThirtyEight blog. You do not have to read or understand this information to complete this assignment, but you may find it interesting nonetheless.
We have given you an implementation of the electoral_college_outcome function, so this section is for your information but you do not need it while writing code for your assignment.
Here is information about US Presidential elections and the US Electoral College, paraphrased from Wikipedia:
The President of the United States is not elected directly by the voters. Instead, the President is elected indirectly by “electors” who are selected by popular vote on a state-by-state basis. Each state has as many electors as members of Congress. There are 538 electors, based on Congress having 435 representatives and 100 senators, plus three electors from the District of Columbia.
Electors are selected on a “winner-take-all” basis. That is, all electoral votes go to the presidential candidate who wins the most votes in the state. (Actually, Maine and Nebraska use a slightly different method, but for simplicity in this assignment, we will assume they use the “winner-take-all” approach.)
Our analysis only considers the Democratic and Republican political parties. This is a reasonable simplification, since a third-party candidate has received an electoral vote only once in the past 60 years (in 1968, George Wallace won 8% of the electoral vote).
This section of the handout explains why poll results are only approximate, and how poll aggregation (combining the results of multiple polls) can help improve accuracy.
Recall that a poll sample is only approximately representative of the voting population. There are two reasons for this: sampling error and pollster bias.
Sampling error is unavoidable, but it can be reduced by increasing the sample size. This is one reason that poll aggregation can be successful: it effectively uses a larger sample than any one individual poll.
In this assignment, you will write a Python program that predicts the outcome of the 2012 US Presidential election, based on polling data and results from the 2012 and 2008 elections. The CSE 160 staff has designed the overall program, including deciding the names and specifications of all the functions and implementing some of the functions. Your job is to implement the rest of the functions. You will verify your implementation using testing code that we provide. Along the way, you will learn about Python collections.
Don't panic! This assignment might look long, but we have already done most of the work for you. You only have to implement 10 functions — and the CSE 160 staff has already written the documentation and tests for those functions, so you know exactly what to do and you know whether your solution is correct. The staff implementation of those 10 function bodies consists of only 63 lines of code in total, and 8 of the 10 functions have a body consisting of 6 or fewer lines of code. Your solution might be smaller or larger, and that is fine; we mention the size only to give you a feel for the approximate amount of code you have to write. While solving this assignment, you should expect to spend more time thinking than programming.
Hint: Before you implement any function, try describing the algorithm in English and hand-simulating it on some sample data. If you need help, ask us! The GoPost is a good place to do so, or you can send email to the staff mailing list.
Obtain the files you need: Downloading the homework5.zip file, then unzip it to create a homework5 directory/folder on your computer.
You will do your work by modifying the file — election.py and then submitting your modified version. Add your name and UW NetID to the top of election.py.
We provide you with the following election data (in the directory homework5/data):
You do not have to open or examine any of these files. The staff has already provided you with all the code that reads files. (It's the read_csv function at the top of election.py; it uses a DictReader from Python's csv library.) You will only write functions that manipulate data structures such as lists and dictionaries.
We describe the files here for completeness, but you can skip the rest of this section if you are not interested.
Each file represents a table, in CSV format: rows are on separate lines, and columns are separated by commas. The first row in each file contains the name of each column. You can open a CSV file using a text editor or using a spreadsheet program such as Microsoft Excel (though a spreadsheet program displays the file differently than its actual contents!). Be careful not to make any changes when examining these files. (Microsoft Excel or another program might encourage you to save the files in a different format; do not do so!)
Each row in the provided polling data (2008-polls.csv and 2012-polls.csv) contains a prediction of the Democratic and Republican popular vote percentages in a single state. Each row also contains the name of the pollster that conducted the poll and the date the poll was conducted.
Each row in the provided election data (2008-results.csv and 2012-results.csv) contains the actual Democratic and Republican popular vote percentages for a single state.
(Note that edges means something different here than it did for graphs!) Let's begin with transforming a list of “election data rows” into a more elegant Python data structure: a dictionary.
Your program will represent the result of a state election in terms of the “Democratic edge”, or the difference between the Democratic and Republican popular vote percentages in that state. For example, if the Democratic candidate receives 53% of the vote (actual or predicted), and the Republican candidate receives 47% of the vote, then the Democratic edge is 6 (percentage points). A positive edge indicates a Democratic lead, and a negative edge indicates a Republican lead. The sign associated with each party is arbitrary — no positive or negative connotation is intended.
Throughout our program, we will frequently need to look up the Democratic edge (hereinafter referred to simply as “edge”) in a particular state. Instead of tediously searching through a list of election data rows to find a particular state and then calculating the edge for that state, let us instead produce a dictionary that maps each state to its edge. The state_edges function creates this dictionary. Read its documentation in the election.py file.
The docstring for state_edges (the triple-quoted text just below the function declaration) is a concise summary of its input parameters and return value, and how they relate to each other. This is known as a function's specification. On first inspection, the specification of state_edges appears too concise: What exactly do we mean by “state edges”?
To avoid confusion about the various data structures used in this assignment, we've given each structure a name, and precisely defined its purpose and representation in Python. A list of these structures can be found at the bottom of this document. There you will find a definition of “state edges”. If you become confused about the parameters or return type of a function, read its specification, and look up any unfamiliar types in the list below. Another way to better understand a given function is to examine its tests that appear in the file tests.py. Those tests don't use exactly the same data as is descibed in the appendix - (often they do not include all keys of a dictionary if they will not be used in the function, or do not use realistic values or the real names of states etc.), but they do use data of a similar type, and you may find the tests' small examples of input and output helpful in understanding a given function.
In election.py, implement the function state_edges. Remove these two lines:
#TODO: Implement this function
pass
and replace them by your implementation. Be sure to take advantage of the provided row_to_edge function.
You do not have to read or examine the .csv files for this or any other problem in the assignment.
For this assignment you will learn a slightly different way of doing testing than we have done in the previous homeworks. In particular, we will not be running election.py to test our code at first - if you do forget and run election.py you will not be making use of the assertions we have set up for you and you are likely to be confused by what you see. Instead we will be running the file tests.py. You should always see these first lines if you are running tests.py:
************************************** **** You are running tests.py ******** **************************************
Take a look at the file tests.py. Read from the beginning of the file up through the code for the function definition of test_state_edges. You will notice that it includes a number of functions called "test_foo" where foo is the name of a function that will be implemented in election.py. Looking inside these functions you will see code similar to what you saw in HW3 and HW4: creation of some sample data structures, followed by several assert statements that test the function foo.
Uncomment the invocation of test_state_edges() near the end of file tests.py. That is, change this line:
#test_state_edges()
to this:
test_state_edges()
Then, run tests.py as a Python program. You can do this by opening tests.py in Canopy, then running while tests.py is the file currently selected. (Alternately, you can type python tests.py at the command line.)
The file tests.py contains Python code that verifies the correctness of each function you write. Every time you finish implementing a function, you should uncomment the corresponding function call at the bottom of tests.py and run tests.py.
If your implementation passes our test cases, then running tests.py will print “Tests passed.” If your implementation is incorrect, an error will be output; in this case, fix your implementation and re-run tests.py, until your implementation passes the tests.
The error produced if your implementation has a bug will not be very helpful. For example, suppose that you run tests.py in Canopy and get an error such as
...
File "tests.py", line 110, in test_state_edges
assert eq(state_edges(rows1), {'WA': 0.9})
AssertionError
This tells you that the value returned by the method call state_edges(rows1) was not {'WA': 0.9} as it should have been, but it does not tell you what the value was. However, if you are running in Canopy, the interpreter now has all of your program's functions defined. You can type:
print state_edges( [{'State': 'WA', 'Dem': '1.0', 'Rep': '0.1'}] )
to the Python interpreter to see the exact value that the call returned. Using the Python interpreter in this way is very convenient: you can perform experiments, calling a function on whatever input you like to better understand its behavior. Of course you can also just type expressions in the interpreter without using the print statement. Keep in mind that that if the expression evaluates to None then nothing will be printed unless you use the expression in a print statement.
Next, we turn our attention to polling data. Election sentiment ebbs and flows in the months leading up to an election, and as a result older polls are much less accurate than more recent polls. In order to prevent old poll data from unduly influencing our prediction of the 2012 election, our program will only consider the most recent poll from a pollster in a state.
Implement the function most_recent_poll_row for this purpose. We provide a function earlier_date, which compares dates formatted as strings. Make use of this function when implementing most_recent_poll_row. If you're stuck, think back to how we found the maximum element in a list. In a sense, most_recent_poll_row is finding the “maximum” of a list of dates. As with any function, if you are having any trouble, step away from the computer, write a set of English instructions, and manually animate your algorithm on some sample data.
Don't forget to uncomment the call of test_most_recent_poll_row at the bottom of tests.py, and run the tests.
Now that we can obtain the most recent poll by a particular pollster in a particular state, we can consider how to represent polling data within Python.
A poll has two pieces of identifying information (“keys”) that we will often want to use to lookup the poll: a state and a pollster. Thus, our Python representation should make it easy to look up a poll given both keys. Nesting a dictionary within another dictionary is a common way to facilitate lookup with multiple keys.
For example, here is a nested dictionary representation, that maps pollsters to state edges, which we call a pollster prediction:
pollster_prediction_example = {
"pollster1": {"WA": 10.0, "OR": 15.0},
"pollster2": {"OR": -5.0, "TX": -15.0}
}
A value can be looked up in a nested dictionary using two pairs of brackets. For example the following code will store the value 10.0 in the variable edge:
edge = pollster_prediction_example["pollster1"]["WA"]
In the above, note that pollster_prediction_example["pollster1"] is a state edge, the dictionary {"WA": 10.0, "OR": 15.0}, that maps states to edges.
Alternatively, we could reverse the keys, and create a nested dictionary that maps states to pollster edges; which we call a state prediction:
state_prediction_example = {
"WA": {"pollster1": 10.0}
"OR": {"pollster1": 15.0, "pollster2": -5.0}
"TX": {"pollster2": -15.0}
}
For example the following code will store the value -5.0 in the variable edge:
edge = state_prediction_example["OR"]["pollster2"]
In the above, note that state_prediction_example["OR"] is a pollster edge, the dictionary {"pollster1": 15.0, "pollster2": -5.0}, that maps pollsters to edges.
Each representation is better suited for different types of lookup. If you have a pollster, and you want to obtain all the state predictions associated with that pollster, the first data structure is most convenient. Conversely, if you have a state, and you want to obtain all the pollster predictions in that state, the second data structure is more convenient. Your program will use both of these representations.
First, implement the helper function unique_column_values. This produces a collection of states and a collection of pollsters to iterate over. You will need this in order to use the most_recent_poll_row function that you previously implemented in Problem 2. As a hint, consider how different Python data structures handle duplicate elements. Looking at the assert statements in tests.py may help you clarify what is being asked for.
Next, implement the pollster_predictions function. Its output produces the first example of nesting described in this problem. (In Problem 5, you will implement a function that transforms one nesting into another.) Your implementation of pollster_predictions will use the helper function most_recent_poll_row that you just implemented.
Don't forget to refer to the data type reference if you are unsure about what data structure to return, and don't forget to uncomment and run the tests.
You are almost done with Part I!
Answer a survey asking how much time you spent on this part of the assignment and other reflections on this part of the assignment.
Submit your work via this: HW5 Part I turnin page.
Now you are done with Part I! On to Part II!
Now that we can represent election results data and polling data in Python, we can begin to implement Nate Silver's algorithm. A first step is to write a function that computes the rank (average error) of a pollster's predictions.
For each state, the error of a predicted edge is the absolute value of the difference between the predicted edge and actual edge. The average error of a collection of predicted and actual state edges is the average of these individual errors for all states the pollster made a prediction for. Implement the function average_error, which computes the average error of state edges for a given pollster. Looking at the assert statements in tests.py may help you clarify what is being asked for.
Hint: Not all pollsters conduct polls in every state. When computing an average error, be sure to divide by the number of states in which a pollster made a prediction, not by the total number of states.
Next, use average_error to implement the function pollster_errors. Again, refer to the data type reference below for more information about parameter and return types. Once completed, pollster_errors provides a quantitative method for measuring the accuracy of a pollster, based on their past predictions.
Recall that in Problem 3, we implemented a function that produces a pollster prediction (a nested dictionary from pollster to state to edge). This nesting was ideal when implementing pollster_errors, however future problems will require the opposite nesting. Implement and test the function pivot_nested_dict, which converts pollster predictions to state predictions.
Hint: the in operator indicates whether a dictionary contains a key.
So far, we have focused on representing election and polling data in Python, and analyzing the accuracy of predictions from past elections. Now, we look to the future!
When predicting the election result in a single state, predictions from multiple pollsters are combined using a weighted average, where a pollster's prediction is weighted according to the accuracy of its past predictions. First, implement and test the helper function weighted_average. A weighted average is defined as follows (images of formulas courtesy of Wikipedia):
For a list of items x:

and a corresponding list of weights w:
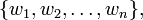
the weighted average of x is:
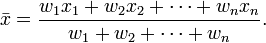
After implementing and testing weighted_average, use it to implement average_edge. We provide the function pollster_to_weight, which you should use to compute the weight of a pollster, based on their average error.
Finally, predict the outcome of the 2012 election! You may find it useful to refresh your memory of the general structure of the FiveThirtyEight algorithm. Don't worry, we have already written most of the code for you. Take a look at the code after Problem 7 in election.py and see how we are calling all those great functions you implemented. Now all we need is for you to implement the function predict_state_edges, which predicts the result of the 2012 election in each state. Make use of the average_edge function from Problem 6 and the pivot_nested_dict function from Problem 5.
Once your implementation of predict_state_edges passes our tests, run election.py as a Python program to predict the outcome of the 2012 election! Do this by typing: python election.py at the command shell. This will print out the predicted edges of each state as well as the predicted outcome of the electoral college.
You should check that your predicted electoral college results (last two lines printed by your program) match the actual outcome of the 2012 election shown below:
Dem 332.0 Rep 206.0
If your program passes all the tests, but does not give this answer, then please send your program to the course staff, who will create an additional test case to help you find your error.
More details about the actual election appear in file data/2012-results.csv and in the Wikipedia article on the 2012 election.
You are almost done!
Make sure to look over election.py and tests.py for any remaining TODO comments (the find feature in Canopy works great). This should help you ensure you have completed the entire assignment.
At the bottom of your election.py file, in the “Collaboration” part, state which students or other people (besides the course staff) helped you with the assignment, or that no one did.
Answer a survey asking how much time you spent and other reflections on this assignment.
Submit your work via this: HW5 Part II turnin page.Now you are done!
A string. Represents a state as its two-letter abbreviation.
state = "WA"
A float. The Democratic edge (difference between Democratic and Republican vote percentages) in a state election.
edge = -5.4
A string. It is the name of a pollster, which is an organization that periodically conducts polls (surveys).
pollster = "Gallup"
A dictionary from State to Edge. Represents the results of either (a) an election or (b) a poll from one particular pollster. The StateEdges for an election will contain an entry for each state, but the StateEdges for a pollster only contains an entry for each state where that pollster conducted a poll.
pollster1_state_edges = {
"AK": -14.0,
"AL": -22.3,
"AR": -23.6,
"AZ": -10.1,
"CA": 20.9
}
state = "AK"
# pollster1_state_edges["AK"] == -14.0
for state in pollster1_state_edges: # Equivalent to: for state in pollster1_state_edges.keys():
print "State:", state, "Edge:", pollster1_state_edges[state]
A dictionary from Pollster to Edge. Represents every pollster's prediction for one particular state.
state1_pollster_edges = {
"MarketShares": 21,
"SouthernIllinoisU": 13,
"IPSOS": 26
}
pollster = "MarketShares"
# state1_pollster_edges[pollster] == 21
for pollster in state1_pollster_edges:
print "Pollster:", pollster, "Edge:", state1_pollster_edges[pollster]
A dictionary from Pollster to StateEdges (from Pollster to State to Edge). Represents a collection of pollsters, each of which has made a prediction for some States (a StateEdges).
pollster_predictions = {
"Gallup": {
"WA": 7,
"CA": 15,
"UT": -30
},
"SurveyUSA": {
"CA": 14,
"CO": 2,
"CT": 13,
"FL": 0,
"GA": -8,
"KY": -14
},
"Omniscient": {
"AK": -14.0,
"AL": -22.3,
"AR": -23.6,
"AZ": -10.1,
"CA": 20.9
}
}
pollster = "Gallup"
state = "WA"
# pollster_predictions[pollster] == { "WA": 7, "CA": 15, "UT": -30 }
# pollster_predictions[pollster][state] == 7
for pollster in pollster_predictions:
print "Predictions for Pollster:", pollster
for state in pollster_predictions[pollster]:
print "State:", state, "Edge:", pollster_predictions[pollster][state]
A dictionary from State to PollsterEdges (from State to Pollster to Edge). For each state, every pollster's prediction for that state (a PollsterEdges).
state_predictions = {
"IL": {
"MarketShares": 21,
"SouthernIllinoisU": 13,
"IPSOS": 26
},
"IN": {
"Rasmussen": -9,
"Howey": -10,
"PharosResearchGroup": -13,
"GlobalStrategy": -6
},
"LA": {
"Zogby": -13,
"SouthernMediaOpinionResearch": -6,
"IPSOS": -2
}
}
state = "IL"
pollster = "MarketShares"
# state_predictions[state] == { "MarketShares": 21, "SouthernIllinoisU": 13, "IPSOS": 26 }
# state_predictions[state][pollster] == 21
for state in state_predictions:
print "Predictions for State:", state
for pollster in state_predictions[state]:
print "Pollster:", pollster, "Edge:", state_predictions[state][pollster]
A dictionary from Pollster to float. Represents every pollster's average error.
pollster1_errors = {
"Gallup" : 6.9,
"SurveyUSA": 3,
"RockyMtnPoll": 0
}
pollster = "Gallup"
# pollster1_errors[pollster] == 6.9
for pollster in pollster1_errors:
print "Pollster:", pollster, "Error:", pollster1_errors[pollster]
A dictionary from string to string. Represents the outcome of an election in a particular state (one row of a spreadsheet-formatted dataset). The keys, which are always "State", "Dem", "Rep", are the names of the columns in the dataset.
Note that in the example below, both keys and values are strings. Even if the value represents a number (such as the number 60.5), it is stored in the dictionary as a string (such as "60.5").
election_data_row = {
"State": "AR",
"Dem": "36.9",
"Rep":"60.5"
}
# Because each ElectionDataRow represents one row of a spreadsheet with many rows,
# you often have a list of rows, which you might call election_data_rows.
# It doesn't make much sense to iterate over this dictionary. Typically you'll have:
for election_data_row in election_data_rows:
print "State:", election_data_row["State"], \
"Dem:", election_data_row["Dem"], \
"Rep:", election_data_row["Rep"]
A dictionary from string to string. Represents the outcome of a poll in a state (one row of a spreadsheet-formatted dataset). The keys, which are always "State", "Dem", "Rep", "Date", and "Pollster", are the names of the columns in the dataset.
Note that in the example below, both keys and values are strings. Even if the value represents a number (such as the number 37), it is stored in the dictionary as a string (such as "37").
poll_data_row = {
"State": "WA",
"Dem": "46",
"Rep": "37",
"Date": "Jul 18, 2012",
"Pollster": "SurveyUSA"
}
# Again, because each PollDataRow represents one row of a spreadsheet with many rows,
# you often have a list of rows, which you might call poll_data_rows.
# Again, it doesn't make much sense to iterate over this dictionary. Typically you'll have:
for poll_data_row in poll_data_rows:
print "State:", poll_data_row["State"], \
"Dem:", poll_data_row["Dem"], \
"Rep:", poll_data_row["Rep"], \
"Date:", poll_data_row["Date"], \
"Pollster:", poll_data_row["Pollster"]