I said that I wanted to write a method called dashes that would take a String as input and that would return a new String with dashes inserted between letters. So given the input "hello", the method would return "h-e-l-l-o".
Someone said that we could build up a temporary String that the method could return. So the basic structure will look like this:
public static String dashes(String s) {
String result = ??
// fill up string
return result;
}
Someone said that we could loop over the characters of the string. Remember
that the string has a method called length that tells you the number of
characters in the string and a method called charAt that gets you the
individual characters of the string:
public static String dashes(String s) {
String result = ??
for (int i = 0; i < s.length(); i++) {
// do something with s.charAt(i)
}
return result;
}
Someone suggested that each time through the loop we want to add to the current
result a dash and the next character, so I modifed the loop to be:
for (int i = 0; i < s.length(); i++) {
result = result + "-" + s.charAt(i);
}
The problem with this is that it would add a leading dash that we don't want.
And putting the dash after the call on charAt would put an extra dash
afterwards. This is a classic fencepost problem that we can solve by
processing the first character before the loop.So we decided to initialize the string to the first character of the word:
String result = s.charAt(0);
Unfortunately, this isn't going to work. You can't assign a string the value
of a character. Someone suggested casting, but that doesn't work either. The
usual way to do this in Java is to append the character to an empty string,
because you can always concatenate a value to a string:
String result = "" + s.charAt(0);
But because we processed the first character before the loop, we had to change
the loop bounds to start at 1 instead of 0. So our final version became:
public static String dashes(String s) {
String result = "" + s.charAt(0);
for (int i = 1; i < s.length(); i++) {
result = result + "-" + s.charAt(i);
}
return result;
}
I mentioned one last detail about this method. It fails in one case. Someone
said that it doesn't properly handle an empty string, which is correct. We
have assumed that there is a character at position 0. That won't work for an
empty string. We could add a special case for that, but I said that in this
case I would probably add a precondition that makes this clear:
// pre: s is not an empty string
It's important to consider these cases and document any preconditions, but
sometimes assumptions like this are reasonable. For example, in the hangman
programming assignment, you will never be asked to deal with an empty string
because the program itself guarantees that all words are at least of length
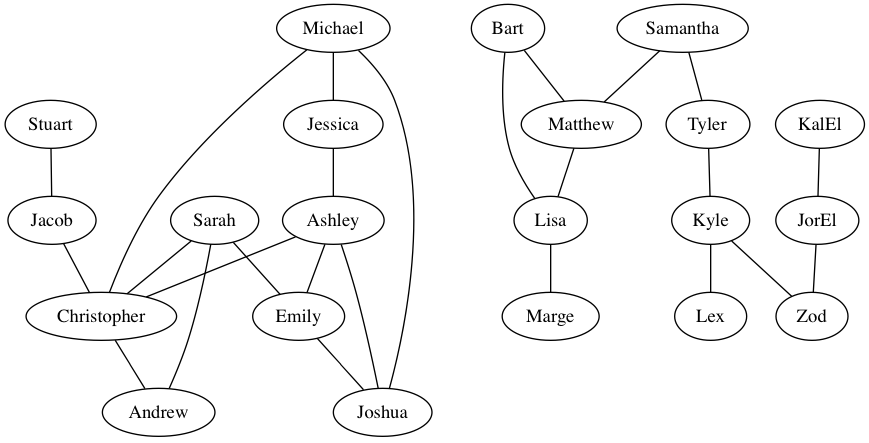
1.Then we continued our discussion of the sample program to find distances between friends. We left off with the idea that we want to have a map that converts a string into a set of string values. Given the name of a person, we can get a Set with the names of that person's friends. For our sample file:
"Andrew" => maps to => [Christopher, Sarah]
"Ashley" => maps to => [Christopher, Emily, Jessica, Joshua]
"Bart" => maps to => [Lisa, Matthew]
"Christopher" => maps to => [Andrew, Ashley, Jacob, Michael, Sarah]
"Emily" => maps to => [Ashley, Joshua, Sarah]
"Jacob" => maps to => [Christopher, Stuart]
"Jessica" => maps to => [Ashley, Michael]
"JorEl" => maps to => [KalEl, Zod]
"Joshua" => maps to => [Ashley, Emily, Michael]
"KalEl" => maps to => [JorEl]
"Kyle" => maps to => [Lex, Tyler, Zod]
"Lex" => maps to => [Kyle]
"Lisa" => maps to => [Bart, Marge, Matthew]
"Marge" => maps to => [Lisa]
"Matthew" => maps to => [Bart, Lisa, Samantha]
"Michael" => maps to => [Christopher, Jessica, Joshua]
"Samantha" => maps to => [Matthew, Tyler]
"Sarah" => maps to => [Andrew, Christopher, Emily]
"Stuart" => maps to => [Jacob]
"Tyler" => maps to => [Kyle, Samantha]
"Zod" => maps to => [JorEl, Kyle]
We had written this code to construct the structure and read in the lines of
input and pull out the individual names:
Map<String, Set<String>> friends = new TreeMap<String, Set<String>>();
while (input.hasNextLine()) {
String line = input.nextLine();
if (line.contains("--")) {
Scanner lineData = new Scanner(line);
String name1 = lineData.next();
lineData.next(); // this skips the "--" token
String name2 = lineData.next();
addTo(friends, name1, name2);
addTo(friends, name2, name1);
}
}
public static void addTo(Map<String, Set<String>> friends, String name1,
String name2) {
if (!friends.containsKey(name1)) {
Set<String> theFriends = new TreeSet<String>();
friends.put(name1, theFriends);
theFriends.add(name2);
} else {
Set<String> theFriends = friends.get(name1);
theFriends.add(name2);
}
}
This code constructs the friends map. I reviewed the code in the addTo method
because it is important to understand how it works as you prepare for the next
homework assignment. This version of the addTo code makes it clear exactly
what is happening in the two different cases. The first time we see a name, we
have to construct a set to keep track of that person's friends and we have to
add a new association to the map and add the friend to that set. If we've seen
the person before, we instead ask the map for a reference to the set of friends
and we alter just the set by adding the friend's name to the existing set. In
this second case, the map doesn't change at all.I mentioned that most programmers would not write the addto method in this way. It is not essential that you understand the more concise way to write it, but I wanted to point out how to shorten the code. Most programmers would not use the local variable theFriends. The addTo code can be shortened to:
if (!friends.containsKey(name1)) {
friends.put(name1, new TreeSet<String>());
friends.get(name1).add(name2);
} else {
friends.get(name1).add(name2);
}
Once it is in this form, you can see that the if/else can be factored to make
this even shorter:
if (!friends.containsKey(name1)) {
friends.put(name1, new TreeSet<String>());
}
friends.get(name1).add(name2);
Then I turned back to the other code we want to write. Once we have the
friends map constructed, we have to use it to find the connection between two
people. I used the example of finding the distance between Jessica and
Stuart:
Starting with Jessica
1 away: [Ashley, Michael]
2 away: [Christopher, Emily, Joshua]
3 away: [Andrew, Jacob, Sarah]
4 away: [Stuart]
found at a distance of 4
We looked again at the friendship map to understand how the program is
computing each of these groups:

To find the friends who are 1 away, we can just look up the entry in the friends map for Jessica because it records the fact that her two friends are Ashley and Michael. Then what?
Someone said that we look at each of Ashley and Michael and find their friends. That generates a new group of people to look at who are two away. As the log of execution above shows, that group includes Christopher, Emily, and Joshua.
We then look at the friends of those three people to find those who are 3 away, and so on. We obviously want to write some kind of loop that finds the people who are 1 away, 2 away, 3 away, and so on. At any given time we will need to keep track of a current group of people who are the current distance away. I asked how to do that and someone said that we could store them in a set.
I asked people how we can get the very first group of people and someone suggested that we can use the friends map to find the people who are 1 away. We can add them to our current group by calling a method called addAll that can be used to add all of the elements of one set to another set. So our code will look like this:
Set<String> currentGroup = new TreeSet<String>();
currentGroup.addAll(friends.get(name1));
int distance = 1;
while (we haven't found the person) {
distance++;
// update group
}
System.out.println("found at a distance of " + distance);
I asked how to know whether we found the person. Remember that at any given
time we have a current group of people that we are considering. And we're
trying to reach a point where we will find name2. So we can test whether or
not name2 is in the current group of people we are looking at:
while (!currentGroup.containsKey(name2)) {
distance++;
// update group
}
So how do we update the group? Remember that we went through everybody in the
current group and added their friends. We can do that with a second set using
a foreach loop to add the friends of each person in the current group. Then we
can reassign the current group to be that new group:
while (!currentGroup.contains(name2)) {
distance++;
Set<String> nextGroup = new TreeSet<String>();
for (String friend : currentGroup) {
nextGroup.addAll(friends.get(friend));
}
currentGroup = nextGroup;
System.out.println(" " + distance + " away: " + currentGroup);
}
When we ran this version, we got the following output:
2 away: [Christopher, Emily, Jessica, Joshua]
3 away: [Andrew, Ashley, Emily, Jacob, Joshua, Michael, Sarah]
4 away: [Andrew, Ashley, Christopher, Emily, Jessica, Joshua, Michael, Sarah, Stuart]
found at a distance of 4
There are some good things about this. It is finding friends at the various
distances, but it is finding them more than once. But it correctly found that
Stuart is 4 away from Jessica.I tried something else. I asked it how far Jessica is away from Jessica and we got this output:
2 away: [Christopher, Emily, Jessica, Joshua]
found at a distance of 2
It is finding that Jessica is a friend of one of her friends. Really it should
say that she is 0 away from herself. We can fix this by changing the way we
initialize the current group. Instead of setting the initial group to be
Jessica's friends who are one away:
Set<String> currentGroup = new TreeSet<String>();
currentGroup.addAll(friends.get(name1));
int distance = 1;
we can initialize it to just Jessica herself and say that she is 0 away:
Set<String> currentGroup = new TreeSet<String>();
currentGroup.add(name1);
int distance = 0;
When we ran this version, it told us that Jessica is 0 away from Jessica and it
gave us more complete information for combinations like Jessica and Stuart:
1 away: [Ashley, Michael]
2 away: [Christopher, Emily, Jessica, Joshua]
3 away: [Andrew, Ashley, Emily, Jacob, Joshua, Michael, Sarah]
4 away: [Andrew, Ashley, Christopher, Emily, Jessica, Joshua, Michael, Sarah, Stuart]
found at a distance of 4
Then we talked about the problem that it is finding the same friends more than
once. For example, look at the log above and you'll se that Ashley is listed
as being 1 away, 3 away, and 4 away. That's because there are various ways to
find this connection from Jessica to Ashley. What we want to do is to consider
Ashley just once instead of considering her multiple times.The solution is to introduce yet another set to keep track of people who have already been explored. Then when we form a new set of friends to consider, we remove the names of people who have already been explored. And each time through the loop we'll have to add the current group to the set of explored people so that we won't explore them in the future. The code below includes the extra lines of code indicated in bold face:
Set<String> alreadySeen = new TreeSet<String>();
Set<String> currentGroup = new TreeSet<String>();
currentGroup.add(name1);
int distance = 0;
while (!currentGroup.contains(name2)) {
distance++;
alreadySeen.addAll(currentGroup);
Set<String> nextGroup = new TreeSet<String>();
for (String friend : currentGroup) {
nextGroup.addAll(friends.get(friend));
}
nextGroup.removeAll(alreadySeen);
currentGroup = nextGroup;
System.out.println(" " + distance + " away: " + currentGroup);
}
System.out.println("found at a distance of " + distance);
There was still one problem left. If it never finds a connection, then it just
keeps searching and searching. So the final change we made was to modify the
loop to exit if the current group ever becomes empty and to report after the
loop that the person wasn't found:
while (!currentGroup.contains(name2) && !currentGroup.isEmpty()) {
...
}
if (currentGroup.contains(name2)) {
System.out.println("found at a distance of " + distance);
} else {
System.out.println("not found");
}
This completes the program.