The slides and textbook reading from the last class discussed the diceRoll example that prints out every combination of rolling n dice. The code for this example is as follows:
// Prints all possible outcomes of rolling the given
// number of six-sided dice in [#, #, #] format.
// pre: dice >= 0
public static void diceRoll(int dice) {
diceRoll(dice, new ArrayList<Integer>());
}
// Prints all possible outcomes of rolling the given number
// of six-sided dice in [#, #, #] format with chosen
// as the prefix of all printed.
private static void diceRoll(int dice, List<Integer> chosen) {
if (dice == 0) {
System.out.println(chosen);
} else {
for (int i = 1; i <= 6; i++) { // for all possible choices
chosen.add(i); // choose
diceRoll(dice - 1, chosen); // explore
chosen.remove(chosen.size() - 1); // unchoose
}
}
}
Reminder
It’s important to remember the bugs we introduced to this program in class:
1) It’s important to remember to remove the choice to “unchoose”.
2) How you remove is important! chosen.remove(i) doesn’t work since it tries to remove at at index i. Even if you could call remove in order to remove a specific value, this won’t work since you want to remove the last instance of the value (the one you just put in). It’s important to remove at the last index instead.
One common way to visualize recursive backtracking is with a decision tree. For the diceRoll example, the decision tree looks like this:
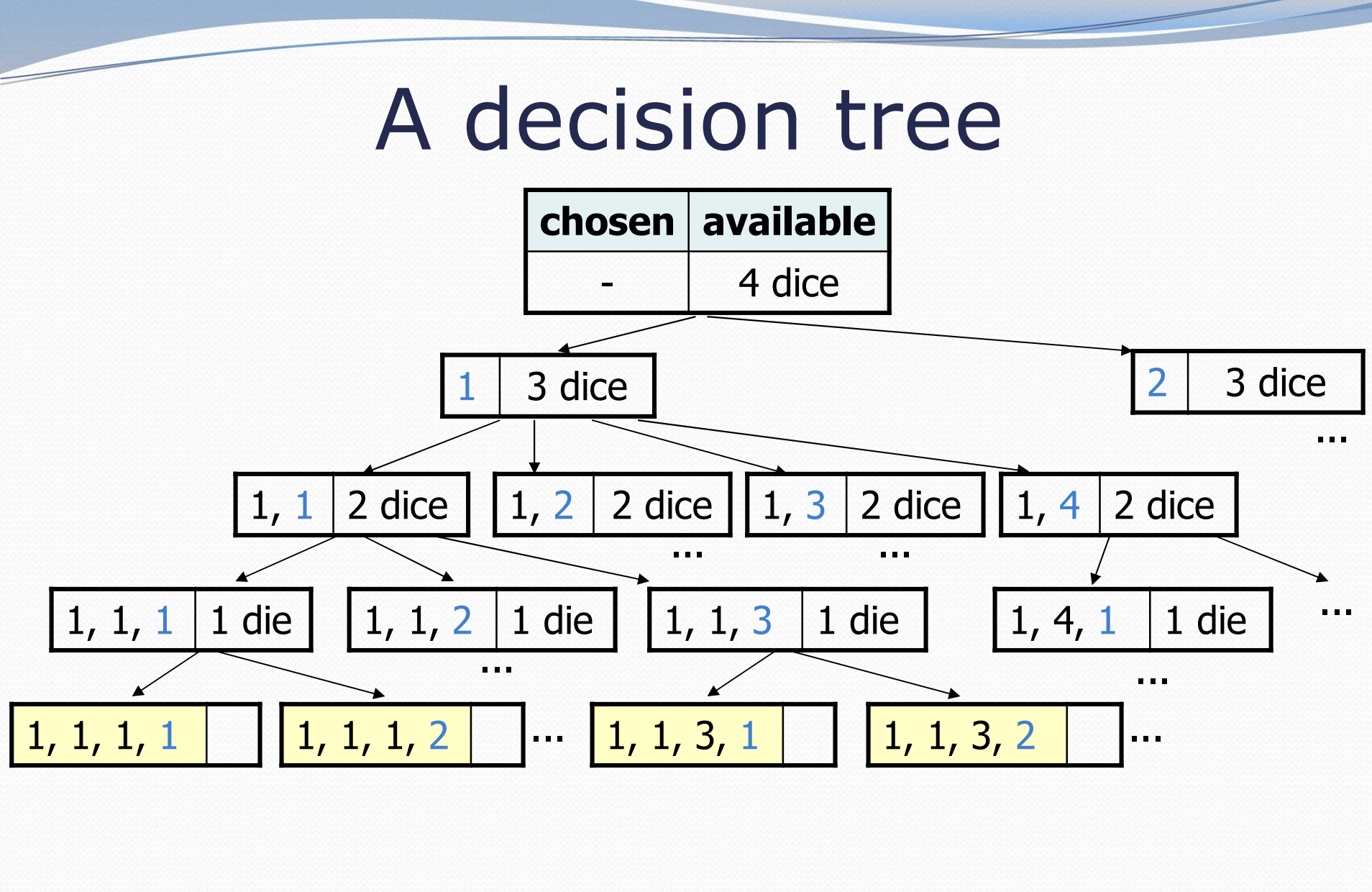
Another common way of trying to see what a recursive backtracking algorithm is doing is to look at a trace of it’s decisions and output. This trace is very similar to the tree picture above, but shows the recursive calls with indentation as well as the choices made at each level.
For example, the trace for diceRoll(0) would be
solution! print []
This happens since we immediately hit the base case.
As a more complex example, here is the trace of decision for diceRoll(2). Notice that each increase in indentation is a recursive call.
diceRoll(2, [])
i=1 -- add 1 to chosen, recurse on diceRoll(1, [1])
i=1 -- add 1 to chosen, recurse on diceRoll(0, [1, 1])
solution! print [1, 1]
i=2 -- add 2 to chosen, recurse on diceRoll(0, [1, 2])
solution! print [1, 2]
i=3 -- add 3 to chosen, recurse on diceRoll(0, [1, 3])
solution! print [1, 3]
i=4 -- add 4 to chosen, recurse on diceRoll(0, [1, 4])
solution! print [1, 4]
i=5 -- add 5 to chosen, recurse on diceRoll(0, [1, 5])
solution! print [1, 5]
i=6 -- add 6 to chosen, recurse on diceRoll(0, [1, 6])
solution! print [1, 6]
i=2 -- add 2 to chosen, recurse on diceRoll(1, [2])
i=1 -- add 1 to chosen, recurse on diceRoll(0, [2, 1])
solution! print [2, 1]
i=2 -- add 2 to chosen, recurse on diceRoll(0, [2, 2])
solution! print [2, 2]
i=3 -- add 3 to chosen, recurse on diceRoll(0, [2, 3])
solution! print [2, 3]
i=4 -- add 4 to chosen, recurse on diceRoll(0, [2, 4])
solution! print [2, 4]
i=5 -- add 5 to chosen, recurse on diceRoll(0, [2, 5])
solution! print [2, 5]
i=6 -- add 6 to chosen, recurse on diceRoll(0, [2, 6])
solution! print [2, 6]
i=3 -- add 3 to chosen, recurse on diceRoll(1, [3])
i=1 -- add 1 to chosen, recurse on diceRoll(0, [3, 1])
solution! print [3, 1]
i=2 -- add 2 to chosen, recurse on diceRoll(0, [3, 2])
solution! print [3, 2]
i=3 -- add 3 to chosen, recurse on diceRoll(0, [3, 3])
solution! print [3, 3]
i=4 -- add 4 to chosen, recurse on diceRoll(0, [3, 4])
solution! print [3, 4]
i=5 -- add 5 to chosen, recurse on diceRoll(0, [3, 5])
solution! print [3, 5]
i=6 -- add 6 to chosen, recurse on diceRoll(0, [3, 6])
solution! print [3, 6]
i=4 -- add 4 to chosen, recurse on diceRoll(1, [4])
i=1 -- add 1 to chosen, recurse on diceRoll(0, [4, 1])
solution! print [4, 1]
i=2 -- add 2 to chosen, recurse on diceRoll(0, [4, 2])
solution! print [4, 2]
i=3 -- add 3 to chosen, recurse on diceRoll(0, [4, 3])
solution! print [4, 3]
i=4 -- add 4 to chosen, recurse on diceRoll(0, [4, 4])
solution! print [4, 4]
i=5 -- add 5 to chosen, recurse on diceRoll(0, [4, 5])
solution! print [4, 5]
i=6 -- add 6 to chosen, recurse on diceRoll(0, [4, 6])
solution! print [4, 6]
i=5 -- add 5 to chosen, recurse on diceRoll(1, [5])
i=1 -- add 1 to chosen, recurse on diceRoll(0, [5, 1])
solution! print [5, 1]
i=2 -- add 2 to chosen, recurse on diceRoll(0, [5, 2])
solution! print [5, 2]
i=3 -- add 3 to chosen, recurse on diceRoll(0, [5, 3])
solution! print [5, 3]
i=4 -- add 4 to chosen, recurse on diceRoll(0, [5, 4])
solution! print [5, 4]
i=5 -- add 5 to chosen, recurse on diceRoll(0, [5, 5])
solution! print [5, 5]
i=6 -- add 6 to chosen, recurse on diceRoll(0, [5, 6])
solution! print [5, 6]
i=6 -- add 6 to chosen, recurse on diceRoll(1, [6])
i=1 -- add 1 to chosen, recurse on diceRoll(0, [6, 1])
solution! print [6, 1]
i=2 -- add 2 to chosen, recurse on diceRoll(0, [6, 2])
solution! print [6, 2]
i=3 -- add 3 to chosen, recurse on diceRoll(0, [6, 3])
solution! print [6, 3]
i=4 -- add 4 to chosen, recurse on diceRoll(0, [6, 4])
solution! print [6, 4]
i=5 -- add 5 to chosen, recurse on diceRoll(0, [6, 5])
solution! print [6, 5]
i=6 -- add 6 to chosen, recurse on diceRoll(0, [6, 6])
solution! print [6, 6]
Notice that this is a ton of output even for a small problem like diceRoll(2).
A very useful skill for helping you write recursive backtracking is identifying how this trace relates to the code that generated it. Some questions you should try to answer to help with this connection:
- Where does the base case appear in the trace?
- How is the number of choices at each level of recursion determined by the code?
- What code needs to be written to modify the parameters for the next recursive call?