Inner class¶

Recall at the end of class, we showed that it’s actually possible to put a class inside of a class! Just like you can define a private helper method, you can also define a private helper class. This is a perfect fit for our IntTreeNode class since it doesn’t make sense for a client to ever have access to a node itself. By making the IntTreeNode defined as private class inside IntTree, only IntTree knows it even exists!

As a technical note that’s reason is outside the scope of CSE 143, we also make this class static since this more appropriately fits our needs. You don’t need to understand why it is static, all you need to know is that you define the node class inside the tree class like we show below.

public class IntTree {
    private IntTreeNode overallRoot;

    // other IntTree methods

    private static class IntTreeNode {
        public int data;
        public IntTreeNode left;
        public IntTreeNode right;
    }
}

IntTree contains¶

A common functionality for objects of binary tree classes and other classes that contain data is to see whether or not they contain a certain value. Let’s give this functionality to objects of our IntTree class by implementing contains, which will return a boolean value depending on whether or not the given int value is in our IntTree. We start with the method stub

// This class represents a tree of integers
public class IntTree {
    private IntTreeNode overallRoot;

    //constructors and other methods

    // post: returns true if the given integer is in the IntTree
    // returns false otherwise
    public boolean contains(int value) {
        // TODO: implement this method
    }

    // This class represents a single node in the tree
    private static class IntTreeNode {
        public int data;
        public IntTreeNode left;
        public IntTreeNode right;

        // other constructors
    }
}

Review of the recursive definition of binary trees¶

In class on Wednesday we learned that binary trees have the following recursive definition:

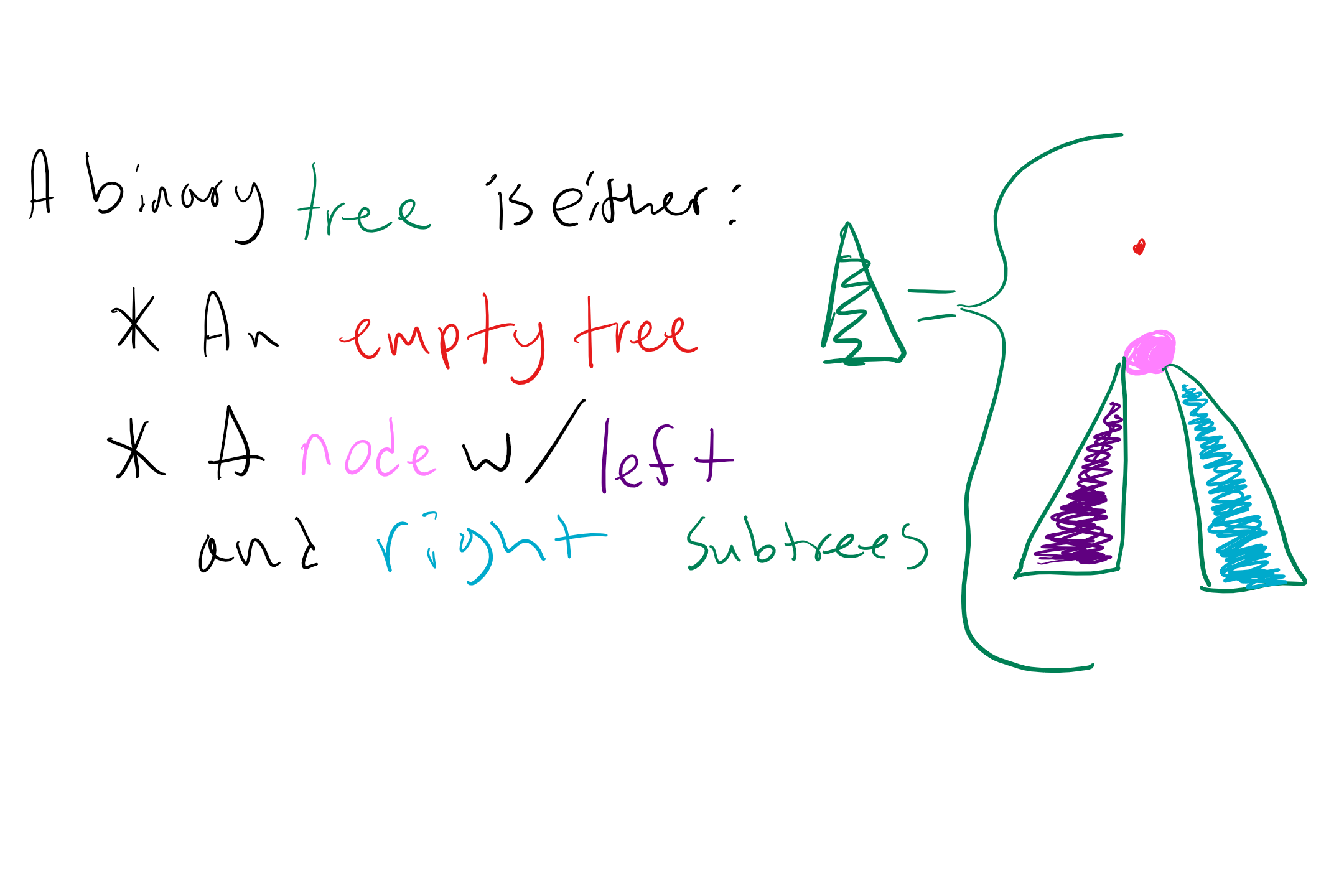
Note how the above tree doesn’t draw out all of the individual nodes in the subtrees, but just draws the subtrees as two more binary trees (which is what they are)! This visualization could help solidify the recursive nature of binary trees, though explicitly drawing out every node could be useful especially when tracing through a solution.

By recalling this definition of binary trees we can see that we might want to implement contains recursively. Since binary trees are recursively defined, we can use the definition to guide us when we implement methods for them. The methods we write will tend to be a bit more readable and concise.

Back to implementing contains¶

Remember, when we write recursive methods we want each method call to represent one small part of solving the larger problem. In this case, we should have each method call represent one instance of the definition of our binary tree. That is, it should either deal with the case where we are at the empty tree, or it should deal with the case where we are at a node with left and right subtrees.

In order to do this, we need some way to keep track of where we currently are in the tree at the time the recursive method is called. Since we have no way of doing this with just the public method, we introduce a private helper method that takes in an IntTreeNode parameter that represents the current node we are at (this is exactly like what we did in the print method in class).

// post: returns true if the given integer is in the IntTree
// returns false otherwise
public boolean contains(int value) {
    // TODO: implement this method
}

// post: return true if the tree starting at the given
// IntTreeNode contains the given value. Returns false otherwise
private boolean contains(IntTreeNode root, int value) {
    // TODO: implement this helper method
}

Now we can begin to write our recursive method. Let’s start with the private helper, which will be doing the bulk of the work. Remember, recursive methods have two parts, a base case and a recursive case. We can use the recursive definition of a binary tree to help us spot what our base case should be and what our recursive case should be. Let’s start with the base case.

Base Case¶

Remember, we want the base case to be the simplest, most basic version of the problem at hand that we can solve almost immediately. What’s a simple tree for which we can immediately tell if it contains our value? The empty tree is simple since we know that the empty tree can’t contain our value. How do we know if a tree is empty? If it is null then we know there are no nodes in our tree, and thus it is empty. We can then signify that it doesn’t contain our value by returning false. The following is a good base case

private boolean contains(IntTreeNode root, int value) {
    if (root == null) {
        return false;
    } else {
        // TODO: implement recursive case
    }
}

Recursive Case¶

Let’s move on to the recursive case, which is when we have a binary tree that is a node with left and right subtrees. When writing recursive cases for binary trees, we need to address each part of the definition. Generally we can think of this todo list, though the specific details will differ depending on the task at hand

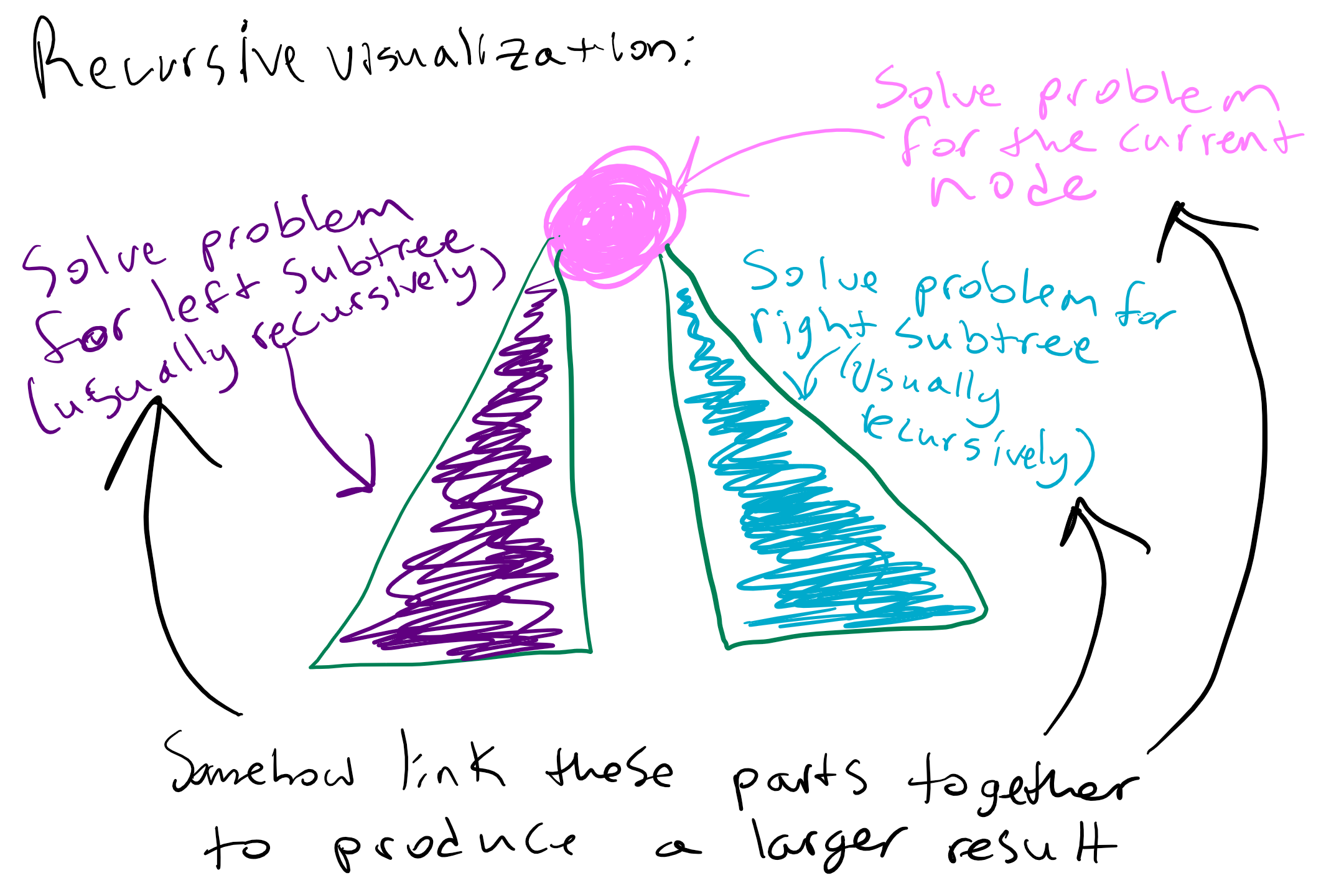
In our contains example, we handle the current node by seeing if it contains the value (i.e. root.data == value), in which case we want to return true to signify that we found the value! Notice in this case we don’t have to recurse because we immediately know the answer. This case checks off the “handle current node” task of our recursive todo list. Our updated method:

private boolean contains(IntTreeNode root, int value) {
    if (root == null) {
        return false;
    } else if (root.data == value) {
        return true;
    } else {
        // TODO: implement recursive case
    }
}

Now we need to handle the left and right subtrees. We know that a subtree is really just a binary tree that starts at either root.left or root.right, so we can see if the value is in a subtree by calling our recursive method on that subtree. This would be a call to contains(root.left, value) for the left subtree and contains(root.right, value) for the right one. Here is a visualization of the recursive case so far

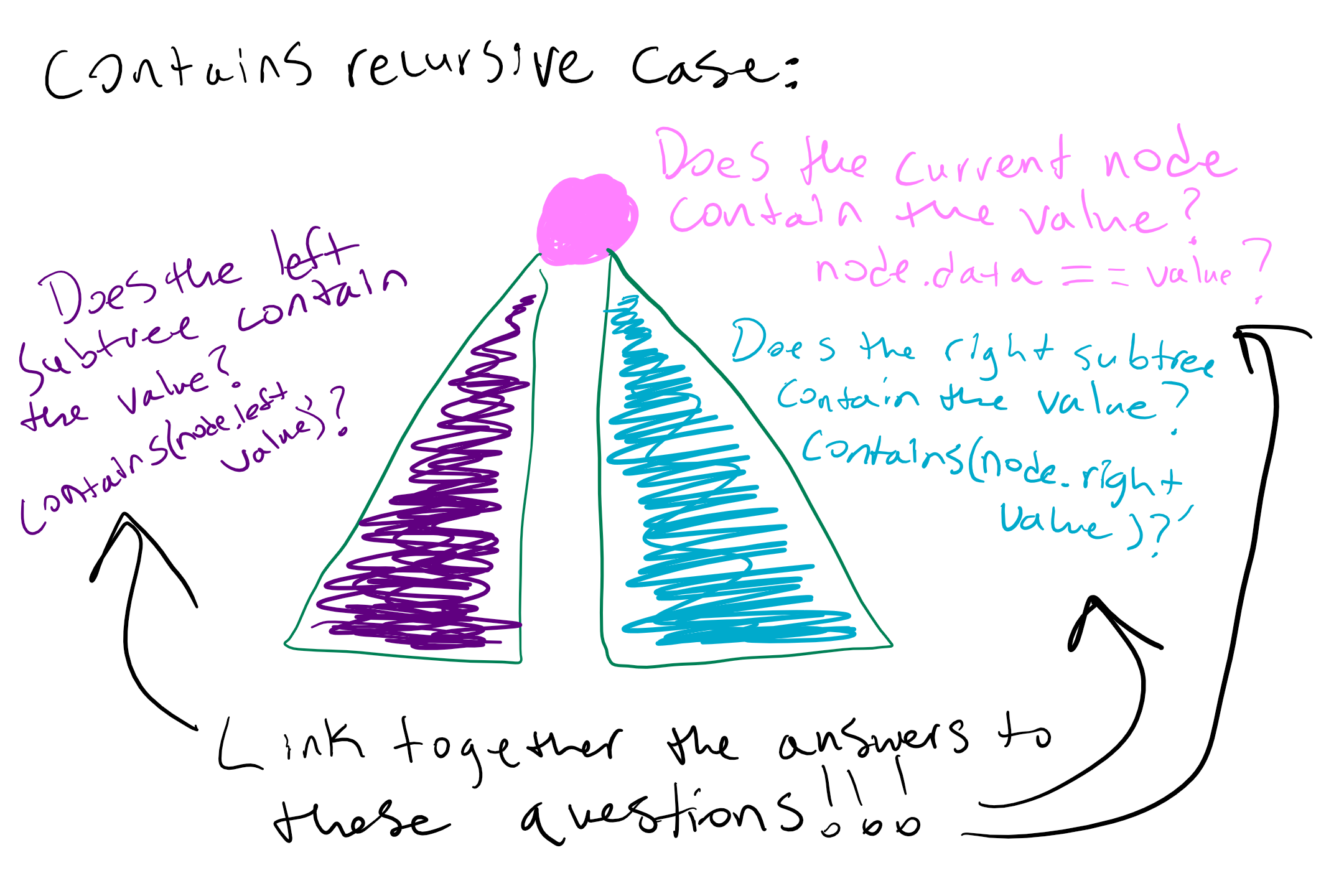
How should we link the two recursive calls on the subtrees together? Now we see the importance of the last bullet point in the todo list above.

Sometimes it can help to describe what we want to return in order to figure out how to link the recursive calls together. If the current node does not contain the value (this means we are in the else branch), then we want to return true if the left subtree or the right subtree contains the value. Thus we can use the logical operator || to complete our private helper method

private boolean contains(IntTreeNode root, int value) {
    if (root == null) {
        return false;
    } else if (root.data == value) {
        return true;
    } else {
        return contains(root.left, value) || contains(root.right, value);
    }
}

Now all that is left is to pair it with the public method! We want to start at overallRoot, so the completed pair looks as follows

public boolean contains(int value) {
    return contains(overallRoot, value);
}

private boolean contains(IntTreeNode root, int value) {
    if (root == null) {
        return false;
    } else if (root.data == value) {
        return true;
    } else {
        return contains(root.left, value) || contains(root.right, value);
    }
}

The most important thing to takeaway from this reading is that we use recursion to solve many binary tree problems because their recursive definition lends itself to more succinct and readable recursive solutions. It’s also important to note that we can use the recursive definition of a binary tree to help guide us when implementing these recursive solutions.

More Practice

Try out this problem and this other problem for more practice with binary trees!