We first introduce some some basic concepts behind one of the oldest and most important areas of computer science and scientific computing, which is known as digital signal processing.
int SAMPLE_RATE = 44100; double[] a = new double[SAMPLE_RATE + 1]; for (int i = 0; i <= SAMPLE_RATE; i++) { a[i] = Math.sin(2 * Math.PI * i * 440 / SAMPLE_RATE); } StdAudio.play(a);
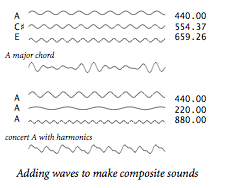
When we add sine waves of different frequency, we can get arbitrarily complicated waves. Indeed, one of the triumphs of 19th century mathematics was the development of the ideas that any periodic function can be expressed as a sum of sine and cosine waves, known as a Fourier series. This mathematical idea corresponds to the idea that we can create a large range of sounds with musical instruments or our vocal chords and that all sound consists of a composition of various oscillating curves. Any sound corresponds to a curve and any curve corresponds to a sound.