CSE589 Lecture 8
November 26, 1997
Scribed by Charla Lambert

Outline of Topics:

• Review of Cryptography.
  terminology
  symmetric cryptography
  public key cryptography
  hybrid cryptosystems
  number theory fundamentals
• The RSA Public Key Cryptosystem.
  primality testing
  factoring large numbers

``Five or six weeks later, she asked me if I had deciphered the manuscript ...I told her that I had. `Without the key, sir, excuse me if I believe the thing impossible.' `Do you wish me to name your key, madame?' `If you please.' I then told her the key-word which belonged to no language, and I saw her surprise. She told me it was impossible, for she believed herself the only possessor of that word which she kept in her memory and which she had never written down.

I should have told her the truth - that the same calculation which had served me for deciphering the manuscript had enabled me to learn the word - but on a caprice it struck me to tell her that a genie had revealed it to me. This false disclosure fettered Madame d'Urfe to me. That day I became the master of her soul, and I abused my power.

From the autobiography of Casanova, 1757

Review of Cryptography

Unlike some fields of science and mathematics, research in cryptography is very easily motivated; one only has to look as far as the known security risks of internet communication:

• Eavesdropping - intermediaries listening in on private conversations. Two solutions to this problem that are currently being used are private and public key encryption systems.
• Manipulation - intermediaries changing information in a private communication. We discuss one-way hash functions as a method for preserving data integrity.
• Impersonation - people communicating under false identification. We discuss digital signatures as one means for providing authentication.

Terminology. Cryptography is the art and science of maintaining security in communication. Cryptanalysis is the art and science of breaking encrypted text.

• Plaintext - the original message.
• Encryption - the process of ``disguising'' the message in order to prevent eavesdroppers from being able to easily read it.
• Ciphertext - the encrypted message.
• Decryption - the process of recovering the original message from the encrypted one.

It is customary to use a cast of characters in discussions on cryptography and protocols of different cryptosystems: Alice wants to send a message to Bob, Eve is eavesdropping on the conversation, Mallory is malicious and wants to actively sabotage the message, and Trent is a neutral third party, trusted by both Alice and Bob.

Symmetric Cryptography. This is an example of private key cryptography where the encryption key can be calculated from the decryption key and vice-versa. The two parties who wish to communicate keep secret the keys and the algorithm which computes one key from the other. Most of the time, the encryption and decryption keys are actually the same, making the protocol for this kind of system very straightforward.

Protocol:

• Alice and Bob agree on a cryptosystem.
• Alice and Bob agree on a secret key.
• Alice encrypts a plaintext using the agreed-upon algorithm and key.
• Alice sends the ciphertext to Bob.
• Bob decrypts the ciphertext with the same algorithm and key.

Advantages: the system is very fast.

Disadvantages: the system requires Alice and Bob to communicate beforehand in order to decide on an algorithm and key. The key must be distributed in secret; if the key is compromised, then the system is broken. Also, if N is the number of parties who wish to communicate with each other, then the number of keys needed grows like .

Public Key Cryptography. In this kind of system, only the decryption key is kept secret. The encryption key is public, and can be published along with the algorithms used to encrypt and decrypt messages. Though it is possible to compute the private/secret key from the public one (and therefore break the system), the hope is that such a computation would take an unreasonable amount of time and patience on the part of any malicious listener.

Protocol:

• Alice and Bob agree on a public key cryptosystem.
• Bob sends Alice his public key, or she finds it in a database or directory.
• Alice encrypts a plaintext using Bob's public key.
• Alice sends the ciphertext to Bob.
• Bob decrypts the ciphertext using his private key.

Advantages: the system does not require Alice and Bob to communicate beforehand. Only the decryption key must be kept secret, and it is kept so by the receiver of messages only, instead of by both the sender and receiver. Each person has associated private and public keys, so that the number of keys needed grows linearly, like , instead of quadratically (as with symmetric cryptography).

Disadvantages: public key cryptosystems can never provide unconditional security. One can always break the system by encrypting every possible plaintext with the public key, thereby matching plaintexts with their corresponding ciphertexts. Also, public key cryptosystems are generally slow, and are vulnerable to chosen-ciphertext attacks.

History: the idea of public key cryptography is due to Diffie and Hellman (1976), and independently to Merkle. The first realization of it came in 1977 with the Rivest, Shamir, and Adleman (RSA) Cryptosystem, and since then, there have been many others. Though RSA is believed to be the most secure and easiest to use among public key cryptosystems, it is by no means the only one. The security of all such systems, however, relies on different computational problems which are believed to be hard:

• RSA - based on factoring large integers.
• McEliecee - based on decoding linear code, which is a proven NP-Complete problem.
• El Gamal - based on the discrete logarithm problem.
• Chor-Rivest - based on the knapsack problem, which is another proven NP-Complete problem.

These problems are all examples of trapdoor one-way functions.

Definition. A function f is called one-way if, given an x, it is easy to compute f(x), but given f(x), it is very difficult to compute x. Trapdoor one-way functions are ones such that, if an additional piece of information y is provided, then, given f(x) and y, then it is easy to compute x.

In public key cryptosystems, it is precisely y which is kept secret; Bob possesses the trapdoor, secret information in his private key, and that is what permits easy inversion of the encryption function.

Hybrid Cryptosystems. In practice, public key cryptosystems are used to secure and distribute session keys, which are then used with private key cryptosystems to secure message traffic.

Protocol:

• Alice finds Bob's public key.
• Alice generates a random session key K.
• Alice encrypts K using Bob's public key.
• Alice sends the ``cipherkey'' to Bob.
• Bob decrypts the message using his private key.
• Alice and Bob communicate using K as the encryption and decryption keys.

A new key K is generated with each new session between communicating parties. This kind of hybrid cryptosystem is much less vulnerable to key discovery than symmetric cryptosystems alone, and it also solves the key-management problem that is inherent to symmetric cryptosystems.

Number Theory Fundamentals. Much of cryptography has foundations in modular arithmetic. Like normal arithmetic, modular arithmetic is commutative, associative, and distributive. However, modular arithmetic allows us to speed up multiplication and exponentiation computations by reducing intermediate results modulo some number:

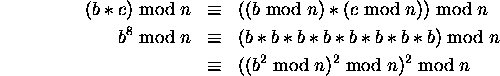
Therefore, requires only k multiplications using modular arithmetic, instead of the multiplications required by normal arithmetic. Since every integer can be written as a sum of powers of 2, the computational time needed for exponentiation is greatly reduced using modular arithmetic.

Definition. Two numbers are relatively prime if they share no common factors. This implies that their greatest common divisor (gcd) is 1.

Definition. The inverse of a number b is x such that . This is also written as . If b and n are relatively prime, then there exists a unique inverse of b modulo n; if b and n are not relatively prime, then there exists no inverse for b. Euclid's Algorithm computes the gcd of two numbers; if , then Euclid's Extended Algorithm can be used to to determine b's inverse.

Definition. For n>1, the Euler totient function, or the Euler phi function (n) is the number of positive integers less than n which are relatively prime to n. If n is prime, then (n)=n-1. If n is the product of two primes, n=pq, then (n)=(p-1)*(q-1).

Theorem. (Fermat's Little Theorem) If n is prime and b is not a multiple of n, then .

(Euler's Generalization of Fermat's Little Theorem) If , then .

These two theorems give a nice form for the inverse of a number - if b and n are relatively prime, then .

Theorem. (The Chinese Remainder Theorem) Given , where for , then the system

has a unique solution modulo M=.

Corollary. If p and q are primes and n=pq, then

This last corollary will prove to be very useful in the RSA Cryptosystem.

The RSA Cryptosystem

Factoring large prime numbers is believed to be a hard problem. The RSA public key cryptosystem takes advantage of this to create a trapdoor one-way function based on the Chinese Remainder Theorem.

Procedure:

• Bob selects at random two large prime numbers, p and q.
• Bob computes n=pq.
• Bob chooses an odd integer c relatively prime to (n)=(p-1)*(q-1).
• Bob computes .
• Bob publishes P=(c,n) as his public key.
• Bob keeps S=(d,n) secret as his private key.

On the domain of possible plaintexts M, the encryption and decryptions functions are: Encryption Function: E(M) = C
Decryption Function: D(C) = M

Proof. To show that this system actually works - i.e., that D()=M - we split the problem into the cases when M and n are relatively prime, and when they are not. Note that if , then cd = k(n) + 1, for some integer k.

Case 1. Assume M and n are relatively prime. Then, with the help of Fermat's Little Theorem,

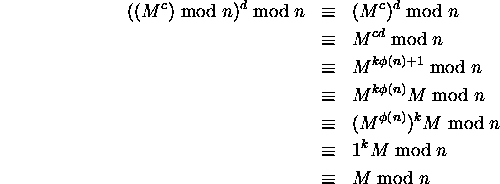
For Case 2, when M and n are not relatively prime, see page 835 of Cormen, Leiserson, and Rivest. The proof uses the corollary to the Chinese Remainder Theorem to show that M is recovered after applying the decryption function to the ciphertext.

Primality Testing. Testing whether a given number is prime turns out to be an NP-Hard problem. Since no deterministic algorithm exists, then a probabilistic algorithm must therefore be used in order to choose p and q in the RSA cryptosystem. Given an integer m which may or may not be prime, we can repeatedly test whether , for randomly chosen numbers b<m. If m is prime, then by Fermat's Little Theorem, this equation will be true for all b chosen. If m is composite, then the equation will be false for more than half of the b chosen.

Procedure:

• Bob chooses a random number b, .
• Bob computes .
• If , then m isn't prime.
• If , then Bob chooses another number and repeats.
• After k iterations, Bob delcares m to be prime. The probability that he is wrong is .

Bob can therefore choose prime numbers with as much confidence as he likes, by iterating the probabilistic algorithm as long as he likes. The probability that the number he eventually chooses is actually composite decreases by a factor of two with every iteration.

Theorem. (The Prime Number Theorem) The number of primes less than a given N is about .

This means that there are about prime numbers that use 512 bits or less of storage space. Primes are plentiful - there is little danger of two people choosing the same primes to compute their public and private keys, and there is even less danger of someone having access to enough space to store a database of all primes.

Factoring Large Numbers. If factoring large integers turns out to be an easy problem, then RSA will be easy to break. However, the converse is unproven. It is only conjectured that if factoring large numbers is hard, then breaking RSA is hard. Therefore, it's imperative that Bob chooses p and q such that n is a very, very, very large number. To date, the best known algorithm for factoring an integer (the number field sieve) has exponential running time in the integer's number of bits: O().

 
• About this document ...