Applied Algorithms Anna Karlin, 426C Sieg
CSE 589, Autumn 1997

Homework # 4
Due November 19

1. You are a traveling salesperson of the 90's. Your boss has asked you to visit n cities, each exactly once, and you are planning your flight itinerary. You do not care about the cost of travel - the company is going to pay your expenses anyway. What you want to maximize is the benefits you will receive as a frequent flyer! In other words, you want to maximize the length of the entire trip. Do not worry about choosing different airlines. You just want to maximize the total mileage. Prove that this problem is NP-complete, and suggest approximation algorithms for it.
2. Prove that the first-fit algorithm for binpacking uses at most twice the optimal number of bins. (The binpacking problem: Let 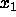, ,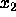..., 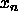be the set of real numbers each between 0 and 1. Partition the numbers into as few subsets (bins) as possible so that the sum of numbers in each subset is at most one. The first-fit algorithm: Put 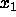into the first bin, and then, for each i, put 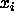in the first bin that has room for it, or start a new bin if there is no room in any of the used bins and put 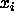in it.)
3. Define a local search strategy for an NP-complete problem other than TSP.
4. Find, by either searching the web, searching the literature, or talking to people a real-life important problem that is NP-complete. It should not be one of the problems that's been mentioned in class. How is the problem solved in practice? (Either find out, or come up with your own idea.)
5. Find, by either searching the web, searching the literature, or talking to people a real-life important problem that is solved using simulated annealing. Explain how the simulated annealing is done e.g., what the solution space and neighborhood structure are, what the cooling schedule is, etc.
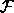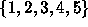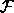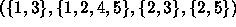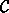
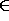
6. Set Cover: An instance of the set cover problem consists of a finite set of elements X and a family of subsets of X. (For example X could be elements and could be . The set cover problem is to find a minimum-size subset 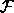whose members contain all the elements of X. (In the example, the first and second sets in 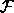(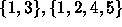) form a set cover because all 5 elements are included in at least one of these sets.)
   • Give a 0/1 integer programming formulation of this problem.
   • Describe (or write pseudo-code for) a branch-and-bound procedure for finding a minimum set cover that uses the linear programming relaxation of the integer program as a basis for pruning the search.
7. An Euler tour of a connected, undirected graph G=(V,E) is a cycle that traverses each edge of G exactly once, although it may visit a vertex more than once.
   1. Show that G has an Euler tour if and only if every node has even degree.
   2. Give an efficient algorithm for finding an Euler tour of a graph if one exists. What is the running time of your algorithm?
8. One can prove that the Vertex Cover problem is NP-hard by showing that Clique polynomially reduces to it as follows. Given an instance of Clique, a graph G=(V,E) and an integer k (such that we're asking if G contains a clique of size at least k), construct the complement graph 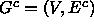. (The edge set 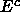of 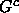consists of precisely those edges which don't exist in E, i.e. 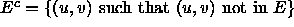.) The output of the reduction is an instance 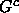, |V|-k of the vertex cover problem. (Is there a vertex cover of size at most |V|-k in 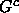?). [Convince yourself that this reduction works!]

   In class we saw an approximation algorithm for vertex cover that finds a vertex cover of size at most twice the minimum size. Does this relationship imply that there is an approximation algorithm with constant ratio bound for the clique problem? Justify your answer!

9. Consider the following closest-point heuristic for building an approximate traveling-salesman tour. Begin with a trivial cycle consisting of a single arbitrarily chosen vertex. At each step, identify the vertex u that is not on the cycle but whose distance to any vertex on the cycle is minimum. Suppose that the vertex on the cycle that is nearest u is vertex v. Extend the cycle to include u by inserting u just after v. Repeat until all vertices are on the cycle. Prove that this heuristic returns a tour whose total cost is not more than twice the cost of an optimal tour.

 
• About this document ...