A projective transformation is the general case of a linear transformation on points in homogeneous coordinates. Therefore, the set of projective transformations on three dimensional space is the set of all four by four matrices operating on the homogeneous coordinate representation of 3D space.
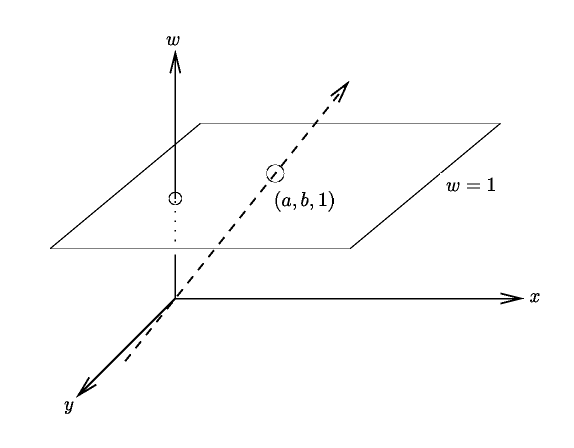
Because projective transformations are so general, little information is necessarily preserved by them. Hyperplanes still map to hyperplanes. Parallelism is not preserved (this is what we would expect, since the perspective transformation can map squares to trapezoids, 'horizontal' lines meeting as they recede with distance). Although ratios are not preserved in the sense of affine transformations, a more general property called the cross ratio is. The running examples and diagrams in this section will refer to a two-dimensional Euclidean space, because that keeps the diagrams drawable, but all the concepts extend to three- (and higher) dimensional spaces. In 2D, we associate the point (a,b) with a set of points in 3D homogeneous coordiates: (wa,wb,w) for all reals w. This corresponds to the heavy dotted line through the origin in the diagram:

Note that the line intersects the w=1 plane exactly at (a,b). We prefer to work in the w=1 plane, since no division is necessary to recover the 2D point from its homogeneous representation if w=1. Unfortunately, this isn't always possible: while affine transformations always preserve w=1, projective transformations don't.
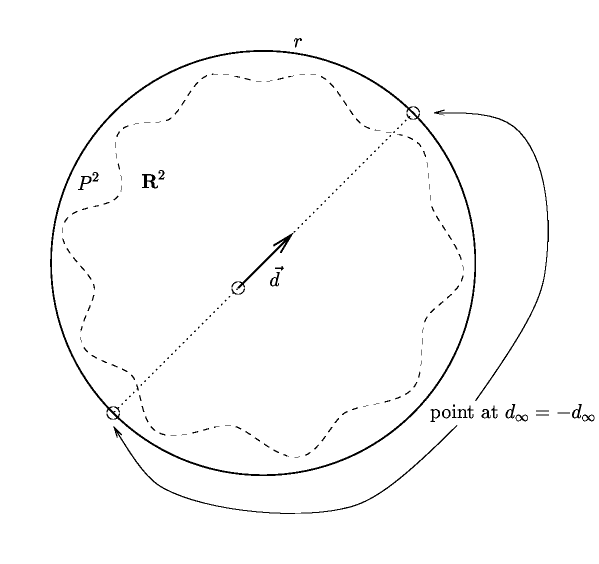
This has some a convenient effect: Every pair of lines intersect in exactly one point. Nonparallel lines intersect in the usual way, while parallel lines in direction d now have an intersection as well: d_inf. Also, every two points (including points at infinity) in P2 determine a line.
Corresponding to each point in the projective plane there is a line in the homogeneous coordinates space, and corresponding to each line in the project plane there is a plane in the homogeneous coordinate space:
q
| PROJECTIVE | HOMOGENEOUS |
| points | lines |
| (a,b) | set of points (wa,wb,w) |
| d_inf | ax+by=0 (a line in direction d in the w=0 plane) |
| lines | planes |
| ax+by+c=0 | ax+by+cw=0 |
| r | w=0 |
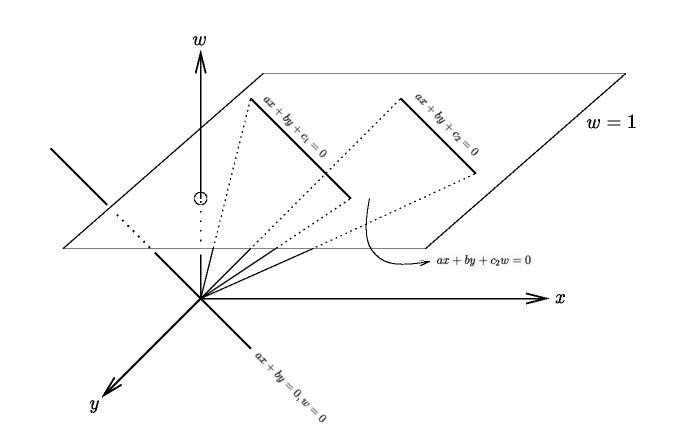
Pretend that the w=1 plane is the projective plane P2. There is a pair of parallel lines lying in this plane: ax+by+c1=0 and ax+by+c2=0. These two lines don't intersect in the ordinary sense, but their intersection in the projective plane is a point at infinity. Let's see what the intersection of their homogeneous counterparts is. Every point on the w=1 plane corresponds to a 3D line through that point and the origin. The two parallel lines thus correspond to two planes. The planes intersect in a line, parallel to the first two, but passing through the origin (and thus lying in the w=0 plane). Back in the projective system, this line corresponds to---the point at infinity which is the projective intersection of the original two lines.
 Previous: Homogeneous = Good |
 Up: Geometric Transformation Index |
 Next: Geometric Transformation Index |