CSE503: Software
Engineering
Lecture 20 (February 24, 1999)
David Notkin
v Slicing
Ø Program slicing is an approach to selecting
semantically related statements from a program [Weiser]
Ø In particular, a slice of a program with
respect to a program point is a projection of the program that includes only
the parts of the program that might affect the values of the variables used at
that point
Ø The slice consists of a set of statements that
are usually not contiguous
v Basic ideas
Ø If you need to perform a software
engineering task, selecting a slice will reduce the size of the code base that
you need to consider
Ø Debugging was the first task considered
Ø Weiser even performed some basic user
studies
Ø Claims have been made about how slicing
might aid program understanding, maintenance, testing, differencing, specialization,
reuse and merging
v Example
read(n)
i := 1;
sum := 0;
product := 1;
while i <= n do begin
sum := sum + i;
product := product * i;
i := i + 1;
end;
write(sum);
write(product);
read(n)
i := 1;
product
:= 1;
while i <= n do begin
product := product * i;
i := i + 1;
end;
write(product);
Ø In this example, the second program is a
slice of the first, slicing on the product variable at the write statement.
v For Weiser, a slice was a reduced,
executable program obtained by removing statements from a program
Ø The new program had to share parts of the
behavior of the original
Ø Weiser computed slices using a dataflow
algorithm, given a program point (criterion)
§
Using data
flow and control dependences, iteratively add sets of relevant statements until
a fixpoint is reached
v Ottenstein & Ottenstein defined an
alternative approach that clearly dominates
Ø Build a program dependence graph (PDG)
representing a program
Ø Select node(s) that identify the slicing
criterion
Ø The slice for that criterion is the
reachable nodes in the PDG
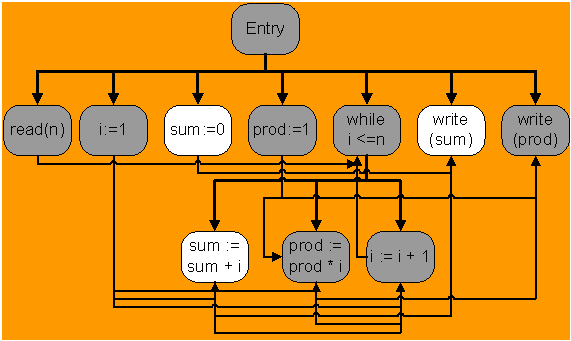
Ø PDG for the example (at the bottom of the
file)
§
Thick lines
are control dependences
§
Thin lines
are (data) flow dependences
v True PDGs are somewhat more complicated
than this
Ø Vertices in the graph represent (a) assignment
states and (b) predicates in the program
Ø Edges represent control and data flow
dependences
Ø Control dependences always start at a
predicate (or the entry node, a special node representing the beginning of the
computation)
§
They are
labeled with a boolean
§
Intuitively,
node w is control dependent on node v if the predicate of node v evaluates to
the label on the edge from v to w
·
That is, what
happens at w controls whether or not v executes
§
An assignment
statement followed immediately by another assignment statement have no control
dependence between them, since the second one always executes when the first
one does
·
This is roughly
similar to the notion of a basic block
Ø Data dependences represent the possible
flow of values through the program
§
(Roughly) there
is a data dependence (edge) from node v to node w if v includes an assignment
to some variable x, and then w includes a use of (that specific) x.
·
These can be
separated into (at least) loop-independent and loop-carried dependences, which
roughly distinguish whether the relationship is across iterations of a loop or
not
Ø Def-order dependences can also be used;
these aren't needed for all analyses, but ensure that only equivalent programs
have isomorphic PDGs.
v Procedures
Ø What happens when you have procedures and
still want to slice?
Ø Weiser extended his dataflow algorithm to
interprocedural slicing
Ø The PDG approach also extends to procedures
Ø But interprocedural PDGs are a bit hairy
(Horwitz, Reps, Binkley used SDGs)
§
Representing
conventional parameter passing is not straightforward
Ø In the Reps/Horwitz paper is an example of
an SDG
program
P := 3.14;
rad := 3;
if DEBUG then rad :=4 fi;
call Mult3(P,rad,rad,area);
call Mult3(2,P,rad,circ);
output(area);
output(circ);
end;
procedure Mult3(op1,op2,op3,result)
result := 0p1*op2*op3;
end;
v Essentially a linked collection of PDGs
(one per procedure), with linking vertices for calling protocols
Ø Value-result parameter passing is used;
it's much harder to handle by-reference mechanisms
Ø If you slice an SDG-like structure using
standard reachability, you can get a very large slice
§
Specifically,
if you slice from inside a procedure, with reachability you trace back to all
possible calls sites of the procedure; since calls and returns are represented
by separate edges, it's roughly like taking a return to a call site that didn't
make the call
§
There are a
number of solutions to this, include the summary edges imposed in SDGs
v Technical issues
Ø How to slice in the face of unstructured
control flow?
Ø Must slices be executable?
Ø What about slicing in the face of pointers?
Ø What about those pesky preprocessor
statements?
v Dynamic slicing
Ø These algorithms have all been static
Ø They work for all possible inputs
Ø There is also work in dynamic slicing,
trying to find slices that satisfy some execution streams over sets of inputs
§
Korel and
Laski characterize dynamic slices in terms of a trajectory that captures the execution history of a program in
terms of a sequence of statements and control predicates
v (Potential) applications of slicing
Ø Debugging
Ø Program differencing
Ø Semantic versions of diff
Ø Program integration
Ø Merging versions together
Ø Testing
§
Slicing can
be used to define more rigorous testing criterion than a conventional data flow
testing criterion
v Recap
Ø Cool idea
Ø Cool supporting technology
Ø Difficult on practical programs
Ø May be coming closer to feasible after almost
20 years of research
Ø Little data on the size of slices
Ø Will it be more than a cool idea?
§
My
guess? No (but I wouldn’t bet the farm
on it)