|
CSE 421, Su '07: Assignment #2, Due: Wednesday, July 4, 2007 |
|
 CSE Home |
About Us |
Search |
Contact Info |
This assignment is part written, part programming. It all focuses on the articulation points algorithm presented in class, and the related problem of decomposing a graph into its biconnected components. I strongly recommend that you do parts 1, 2 and 3 before you start the programming portion, and do them soon so you have time to ask questions before you get immersed in coding.
A vertex in a connected undirected graph is an articulation point if removing it (and all edges incident to it, i.e. touching it) results in a non-connected graph. As important special cases, a graph having a single vertex has no articulation points, nor does a connected graph having just two vertices (which of course must be joined by an edge, otherwise it isn't connected).
A connected graph is biconnected if it has no articulation points. A biconnected component of an undirected graph G = (V,E) is a maximal subset B of the edges with the property that the graph GB = (VB,B) is biconnected, where VB is the subset of vertices incident to (touched by) edges in B. (Maximal means you can't enlarge B without destroying its biconnected property.)
Above, I noted that a graph consisting of single edge is biconnected. Consequently, every edge in G is part of some biconnected component. In fact, every edge is part of exactly one biconnected components. (This really needs a proof, which you don't need to give, but basically it's true because if some edge were in two components, their union would also be biconnected, contradicting the "maximality" condition.) So, the biconnected components partition the edges. Another fact, just to help your intuition: in a biconnected component, any two distinct edges lie on a common simple cycle. (This motivates the term "biconnected"---there are always two independent paths between places. Again, these statements need careful proof, but the idea is simple: if there weren't two paths, you could disconnect the graph by removing some vertex on the one path.)
For example, the biconnected components of this graph
are the five sets of edges:
There is a very close relationship between biconnected components and articulation points. Namely, the articulation points are exactly the vertices at which two biconnected components are connected. Given this fact, it shouldn't be a big surprise that there is a linear time algorithm that identifies the biconnected components of a graph, and in fact this algorithm is quite similar to the articulation point algorithm.
Simulate on the graph shown on the right
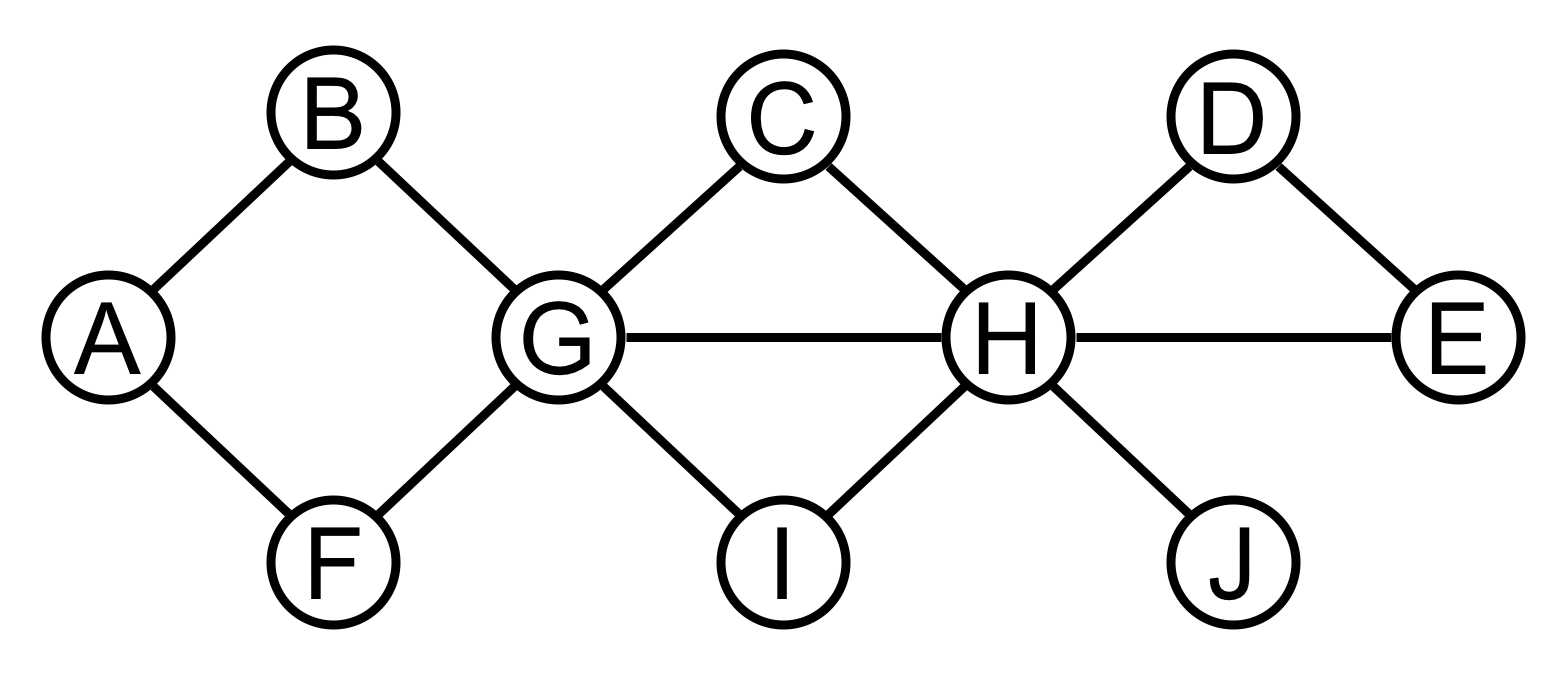the algorithm presented in class for finding articulation points.
Redraw the graph clearly showing (a) tree edges, (b) back edges,
(c) the DFS number and (d) LOW value assigned to each vertex, and
(e) identify the articulation points. In addition, (f) list the
edges in the order that they are explored (i.e., traversed for the
1st time) by the algorithm. For definiteness, start your DFS
at vertex C and whenever the algorithm has a choice of
which edge to follow next, pick the edge to the alphabetically
first vertex among the choices.
Find and list the biconnected components of the graph in problem 1.
Give a modification of the articulation-points algorithm that finds biconnected components. Describe the algorithm (in English; should only take a few sentences). Simulate it on the example in problem 1, showing enough of a trace of the algorithm's execution to demonstrate that it finds exactly the components you found in problem 2. [Hints: look carefully at the order in which the articulation points algorithm in part 1 explores edges and discovers articulation points, and relate this to which edges are part of which biconnected components. Among other things, you might want to circle or otherwise mark the biconnected components on the edge list you produced as part of your solution to problem 1. Initially, focus on the first biconnected component to be completely explored by the depth-first search.]
Implement, test, and time the algorithm you found in problem 3.
Input format: To keep things simple, assume the input will consist of a positive integer "N" followed by some number of pairs of integers in the range 0 to N-1. "N" represents the number of vertices in the graph, and each pair u v represents an edge between vertices u and v. Although a good program really should check for the following malformed inputs, you may simply assume that you never get: negative numbers, numbers outside the range 0 to N-1, an even number of integers in total (i.e. the last pair is unfinished), or a pair u v where u=v, or where either (u,v) or (v,u) duplicates a previous pair in the list.
Output Format: Print out the number of nodes, number of edges, number of biconnected components, number of articulation points, list the articulation points, list the edges in each biconnected component, and the algorithm's run time (excluding input/output; see below).
Implementation: I don't care much what programming language you use; C/C++/C#, Java, Perl, Python, Ruby all seem reasonable (ask otherwise). You should use some flavor of edge-list representation so that your algorithm is faster on sparse graphs, but I recommend keeping this as simple as possible. In particular, you may use built-in or standard library packages for hash tables, lists, dynamic arrays, etc. for the edge lists so that you don't need to spend a lot of time duplicating all that fun linked list code you wrote in 143/326. Since the time spent reading the graph is excluded from your timing study (below), it's OK if the data structures are somewhat slow to construct, just so you can efficiently traverse all the edges as needed by the main algorithm. Also, you do not have to obey anything like the "order edges alphabetically" convention I use on by-hand examples -- just traverse them in whatever order comes naturally for your data structure.
Timing: Also run it on a variety of graphs of different sizes and different densities (average number of edges per vertex) and measure its run time on each.
Write a brief report (2-3 pages, say) summarizing your measurements. Include a graph (old fashioned scatter plot) of run time versus problem size. You might plot time versus vertices or time vs edges or time divided by vertices vs vertices plus edges, etc. Which do you find most informative? Explain why. Fit a "trend line" to the data (e.g. with Excel). Compare to the theoretical big-O bounds for your sample graphs. Are your observations in line with the dogma we spout about the utility of big-O analysis? Are there discrepancies? Can you explain them? Does number of edges versus number of vertices have any bearing on performance? Also, if possible, give us a quick summary of the kind of processor on which you ran your timing tests. E.g., "233 Mhz Intel Pentium II with 64k cache and 96Mb RAM."
To simplify your job doing the timing measurements, we have provided a program that generates random graphs of various sizes in the specified input format.
Two hints on timing measurements: Record separately or exclude from your timing measurements the time spent reading inputs, since this may dominate the interesting part. Similarly, except for the summary parameters giving numbers of vertices, edges and components, you may want to disable output formatting and printing during you timing runs. See also the FAQ page for other timing tips.
Turn In: Given the holiday next week, I strongly recommend you turn in at least problems 1-3 in class on Monday (or, if necessary, to my office on Tuesday by 4:00 PM. In any event, turn in your code via the Catalyst link below. Whatever you don't turn in physically, you can turn in electronically with your code, by 4:00 PM Wednesday 7/4, by bundling all your files in a single tar or zip archive, submitted to the Catalyst link below. Handwritten parts may be scanned (.tiff, .gif, .jpeg, .ps, .pdf), or you may use drawing tools in powerpoint, etc. For prose, plain text is fine (sub/superscript as x_2/x^2, e.g.), as is word, .rtf, .doc, .ps, .pdf. I don't have the latest Office, so please avoid their new .xml-based formats.
Also describe and implement any other algorithm you like for solving the problem, e.g. this simple but slow one: As mentioned, two (different) edges are in the same biconnected component if and only there is a simple cycle in G that includes both. So, you could do something like this: for every pair of edges, try to find a path from one to the other (maybe by DFS or BFS), and then try to find a path back, excluding the edges in the path already taken.
 |
Computer Science & Engineering University of Washington Box 352350 Seattle, WA 98195-2350 (206) 543-1695 voice, (206) 543-2969 FAX |