Project 3 Raindrops Keep Falling
The topic for this project is the modeling of the physical world. You will begin with a simple program to model raindrops falling on pavement, and embellish it and experiment with it. The purposes of the assignment are (a) to illustrate how computers are used to model the world, (b) to experiment with a model to observe how its different characteristics affect the result and (c) to understand how the simplifying assumptions of the model affect the answers.
A simplified model
The VB code shown below is a simple model of raindrops falling on pavement. The "pavement" is a 2000x2000 unit square region with coordinates (1000,1000) to (3000,3000). The size and coordinates were arbitrarily chosen; the main criterion was to make it easy to display the situation to help the experimenters. The program places circles, representing raindrops, into the region at random locations. The circles have random radii ranging from 100 to 200 units. An illustration of the situation is as follows, after 100 drops have been placed into the region:

The program determines how many raindrops it takes to get the pavement completely wet, which is defined to be the situation in which every part of the pavement is covered by a raindrop. By the selection of the sizes the results should apply to raindrops falling on square areas in which the drops have radii from 1/10th to 1/20th of the length of the side of the area. The following text describes the program.
The Given Program
In order to keep track of which portions of the pavement are wet, the raindrops are stored in three arrays,
Dim xCoord(2999) As Integer, yCoord(2999) As Integer
Dim rad(2999) As Integer
The first two keep track of the coordinates of the center point of the raindrop, and the third stores the radius of the raindrop. The size of the arrays is estimated to be large enough to store all of the circles required for the experiments proposed. Of course, the storage scheme is that the ith circle has its coordinates stored in
xCoord(i), yCoord(i) and its radius stored in rad(i). The arrays are filled from the beginning, and will usually only be partially full. To keep track of the largest index position used so far, and to allow indexing into the arrays, two integers are declared,Dim nMax As Integer, index As Integer
Only
nMax need be initialized because index will be initialized prior to each loop in which it is used.As explained in lecture it is not possible to check the infinitely many points of the region to see if they are covered by one or more droplets, so a methodical process is used to check the pavement at regular intervals. Starting at the 1000,1000 position and continuing to 3000,3000, moving in units of
delta in each direction, the program examines whether a droplet covers the position. These are known as grid points. In order to keep track of the grid points being checked three integers are declaredDim gPointx As Integer, gPointy As Integer, delta As Integer
The values of the first two variables will range from 1000 to 3000; delta will be set to 4.
After initializing the variables and drawing a square to represent the pavement, the program generates the first drop. For this and the other drops, a circle is drawn in the square, but this is not an accurate rendering of the drop. Rather, it is a small circle representing the center point and it is drawn simply to give feedback as to the progress of the model. (If the circle were drawn to size, the area would quickly be covered, and appear to be wet.) Once the first drop has been generated, the program enters a doubly nested loop that visits each grid point, checking if it is covered by some drop. (The logic of this process was explained in lecture.) At the conclusion of the computation the total number of drops computed (
nMax+1) is reported in a label called lblAmtHere is the code:
.
Private Sub Form_Load()
Randomize ' Gives ever changing random numbers
End Sub
Private Sub Form_Click()
Call rainDrop
End Sub
Private Sub rainDrop()
' This program analyzes how may raindrops it takes to get the
' pavement wet
Dim xCoord(2999) As Integer, yCoord(2999) As Integer
Dim rad(2999) As Integer
Dim gPointx As Integer, gPointy As Integer
Dim index As Integer, nMax As Integer
Dim delta As Integer
Dim found As Integer 'found a spot occupied by a rain drop
' Initialize the variables
gPointx = 1000
gPointy = 1000
delta = 4
nMax = 0
FillStyle = 0
found = 0
' Draw a 2000x2000 box representing the pavement
FillColor = RGB(255, 255, 255)
Line (1000, 1000)-(3000, 3000), , B
' Set the initial drop and draw it
xCoord(0) = Int(Rnd(1) * 2000) + 1000
yCoord(0) = Int(Rnd(1) * 2000) + 1000
rad(0) = Int(Rnd(1) * 100) + 100
FillColor = RGB(0, 0, 255)
Circle (xCoord(0), yCoord(0)), 20, RGB(255, 0, 0)
' Loop, checking the grid points to see if they are wet, and if
' not, generate drops until they get "hit"
Do While gPointy < 3000
Do While gPointx < 3000
Call check(xCoord(), yCoord(), rad(), nMax, gPointx, gPointy, found)
If found = 1 Then
gPointx = gPointx + delta
Else
nMax = nMax + 1
xCoord(nMax) = Int(Rnd(1) * 2000) + 1000
yCoord(nMax) = Int(Rnd(1) * 2000) + 1000
rad(nMax) = Int(Rnd(1) * 100) + 100
Circle (xCoord(nMax), yCoord(nMax)), 20, RGB(0, 255, 255)
End If
Loop
gPointx = 1000
gPointy = gPointy + delta
Loop
FillColor = RGB(255, 0, 0)
Circle (xCoord(nMax), yCoord(nMax)), rad(nMax), RGB(0, 255, 255)
lblAmt.Caption = "Total Drops " & nMax + 1
End Sub
Private Sub check(x() As Integer, y() As Integer, r() As Integer, nMax As Integer, xpt As Integer, ypt As Integer, found As Integer)
Dim index As Integer
index = 0
found = 0
Do While index <= nMax And found = 0
If r(index) > ((x(index) - xpt) ^ 2 + (y(index) - ypt) ^ 2) ^ 0.5 Then
found = 1
Else
index = index + 1
End If
Loop
End Sub
An example run for the
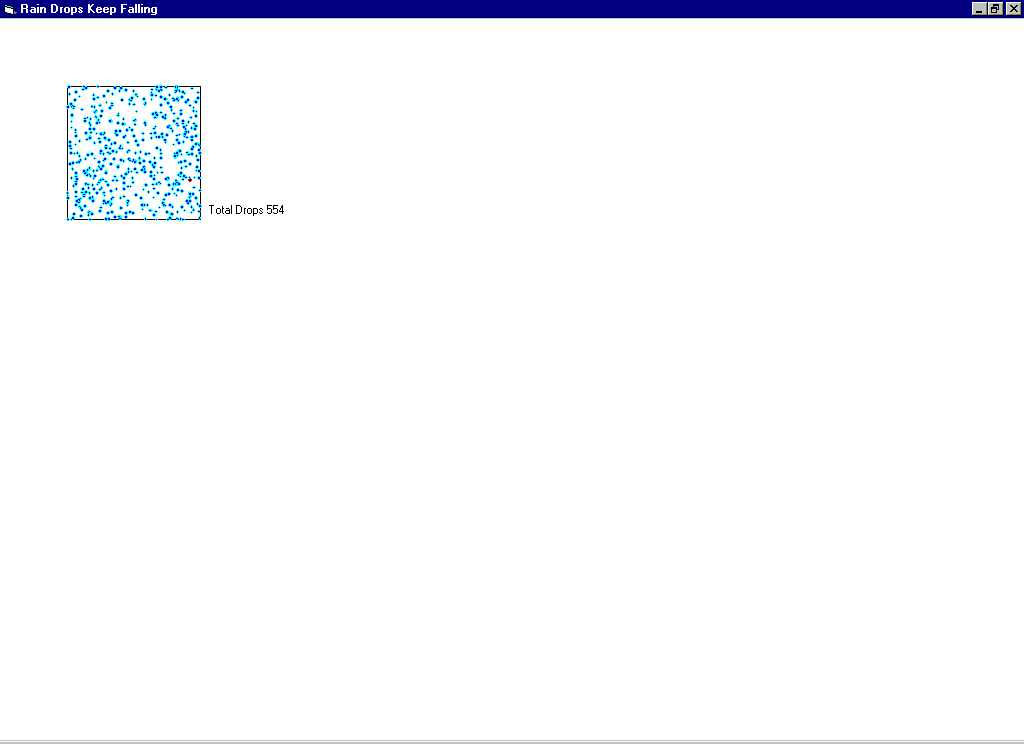
A Physical Model
Study the
rainDrop procedure and understand its logic. Then type the program into VB and try it out. (Typing the program into VB is a requirement of this project; you are asked to do so as an aid to studying its logic.) Notice that the program assumes a white form that has its WindowState set to 2 (set it in the Properties list, not in the program) and it uses a label, lblAmt to print out the count. Run the program just to be sure you didnít make any typos in entering the program.To make the experiment more intuitive, draw the drops on the pavement.
Task 1: Change the two
Circle drawing calls in the program so that they use as their radius the actual radius generated for the drop, i.e. rad, rather than the 20 unit radius used to illustrate the center point.
Run a few experiments. It may take up to a minute before the answer comes back. Why does it take so long? The main reason is that we are checking many grid points. How many? The side of the pavement square is 2000 units, and the program checks every 4 units:
2000/4 = 500
Thatís 500 checks per row for 500 rows, yielding
5002 = 250,000
Thus, a quarter of a million checks are made and for each one we must run through the whole list of circles generated to that point. Is this really necessary? If we raise
delta to be 20, we have a coarser grid. This reduces the number of checks to 10,000, since now there are 100 checks in 100 rows. Try changing delta to 20 and notice how much faster the program is. Try it for other values, say 50 and 100.Run the program a few times. It appears that many, many more drops are being generated than are necessary. Does the program have a bug in it? Probably not. What is happening is that although it appears that raindrops already cover the area, there are a few places in our grid where drops come very close, but do not touch.
When we check these spots, we find out Ė correctly Ė that they are dry. These cases are not visible at the resolution of the computer monitor. We generate drops until this spot is covered. Of course, meanwhile, the random nature of the drops is such that many other places are getting covered over and over again while the dry spot continues to be missed. This effect is actually visible if
delta is raised to 200. (It may take a couple of experiments before one shows a white region not covered by a drop.)Precision
The conclusion from changing
delta is that the program runs faster when delta is larger, but apparently the quality of the answer might not the same, since white space was noticeable when delta was very large. This is a standard aspect of modeling the physical world: When is the experiment detailed enough to be "right"?To examine this question, begin by disabling the
Randomize call in the Form_Load procedure by placing a comment quote in front of it. (The line will turn green.) Commenting out Randomize will have the effect of starting the random number generator at the same place every time the program is run. In this way, the same sequence of drops can be generated for different values of delta.Task 2a: After commenting out the
Randomize call, run trials with delta values equal to 8, 16, 32, 64, 128, recording the number of drops for each run. This constitutes on experiment for this task.What should have happened is that the smaller delta value experiments all got a larger number of drops than the larger delta value experiments and the numbers are all the same. The smaller delta values are more accurate, since they assure that the tinier regions are all wet. Of course, we would like to use the largest value of delta that gets the "right" answer. From the Task 2a experiments, it is possible to conjecture what that number would be. But, unfortunately, it is not possible to generalize from just one experiment.
Running more experiments is necessary, but the random number generator will always start at the same place, meaning that weíll always get the same set of drops. Nothing will change. This problem can be by-passed by "spinning" the random number generator (generate random numbers and throw them away) before starting the experiment. If we "spin" for a given amount before each experiment, all trials will check the same sequence of drops. If we "spin" for a different amount before each experiment, it will use a different sequence of drops.
Task 2b: Declare integer variables, spin and throwAway, and program a loop using spin as the iteration variable. In the loop increment spin, and generate a random number and assign it to throwAway. Run the trials of Task 2a for spin amounts of 5000, 10000, 15000 and 20000. To spin for 5000 numbers, the termination condition of the loop will need to be spin < 5000, assuming it starts at 0, and this must be changed for each experiment along with delta. Record the number of drops for each value of delta.
As you run the Task 2b experiments, keep in mind that it is possible to have delta be smaller and smaller and smaller. With each "halving" of the size, the solution takes approximately four times longer to run because there are four times as many points. Yet, there is no limit to how small delta can get because there will always be cases where drops seem to be touching for delta, but are not touching for delta/2.
Task 2c: Write a paragraph describing the results of Task 2b. Pick the value of delta that you think is optimal, and justify why you are choosing it. Include a list of your experimental results.
Set delta to its optimal value. "Uncomment" the Randomize call.
Good To The Last Drop
It is interesting to see the location of the last drop generated. It is possible to display this drop.
Task 3: Draw the last drop added to the list by drawing at the end of the procedure the last raindrop, i.e. the one with index
nMax. Redrawing this drop in, say, red will make it very visible.Run the program a few times and notice where the last drop "falls". There probably isnít a pattern to where it is, except that it is not in the lower right corner, i.e. at the last grid point checked. In fact, it is often towards the top. Why? Also, notice the bursty behavior. That is, when the program starts there is a burst of drops displayed. Then, many times there is a pause, then another burst. Then another pause, perhaps, and the red drop is displayed. What is causing this unusual behavior?
Task 4: Write a paragraph explaining in your own words why it might be that the red drop tends to be near the top of the region. Also, write a paragraph explaining in your own words why the program tends to work in bursts.

Notice that although multiple drops cover many of the points on the pavement, there is a point somewhere under the last drop that is covered by only one. This is the grid point (
gPointx, gPointy) when the last drop was generated. (It is not (likely to be) the center of the last drop, however.) Check that this point is covered by only one drop.Task 5: Modify the
rainDrop procedure to save the coordinates of the (dry) grid point being processed when each newly drawn drop is generated. You must declare the integer variables to save these values in. Resaving the grid point coordinates each time a new drop is generated will work out, since the coordinates saved the very last time are the ones of interest. At the end of the rainDrop procedure, set up a loop like the check procedure to count how many drops overlap the saved point. You will have to declare one more integer variable to count up the number overlapped. Add a label and display the result of the count.Run a few experiments. Does only a single drop always cover the last dry grid point? If not, then there is a bug somewhere in your program.
It would be interesting to see what the maximum depth of drops is that covers any spot on the pavement, and to know what the average depth of drops is. To discover these statistics, we will change the solution to Task 5 to keep track of the depth of drops covering various points on the pavement. We wonít check every delta units, however. Instead, we will sample at different points on the pavement, say every 100 units. Though this sampling may not be as fine grain as the modelís constraints, i.e. 100 > delta, it should be accurate enough to give a good description of how deep is the water.
Task 6a: Modify the Task 5 solution as follows: Add an array dropNum of 100 integers to be used to keep track of the number of drops covering grid points, i.e. dropNum will contain the number of grid points covered by a single drop. Initialize dropNum to 0s. [dropNum is used to specify this assignment; you must select another name and it cannot be numDrop!] Then, using coordinate variables you declared in Task 5, write a doubly nested loop at the end of the rainDrop procedure to count for each coordinate position on a 100 unit spacing the number of drops that overlap that point. (This is like Task 5, but for all points on a 100-spacing grid.) If the count is x, then increment dropNum(x). Print out a histogram of the results by looping through dropNum using the following loops:
index = 0
Do While index < 100
index2 = dropNum(index)
Do While index2 > 0
Line (1000, 3300 + index * 200)-(1000 + index2 * 200, 3300 + index * 200 + 200), RGB(255, 255, 255), B
index2 = index2 - 1
Loop
index = index + 1
Loop
(Note the new integer variable,
index2, which must be declared.) Finally, change the label added in Task 5 so that it prints out the maximum depth, i.e. the largest index of the largest nonzero entry in dropNum, i.e. the greatest depth of drops. Run the program and get a screen that has the following form:
To compute the average depth of drops, we analyze what one of the red boxes means. A box in the ith row means that a sampled grid point was found to be covered by i raindrops. There were
(2000 / 100) x (2000 / 100) = 20 x 20 = 400
points sampled. So, to compute the average depth of drops over the whole region, we need to multiply the number of boxes in each row times which row it is, add those values together and divide by 400.
Task 6b: Add the necessary program text to the end of the
rainDrop procedure to compute the average depth of raindrops over the region. Display the average along with the maximum displayed in Task 6a. Remember that the average may have a decimal fraction, so it should be declared as a double.
Remember that the average may have a decimal fraction, so it should be declared as a double.
An Improved Model
When one has a physical model, it is usually used to learn something about the phenomenon. In the present case we are interested in the number of raindrops that it takes to cover the amount of pavement being studied. This can be determined by running experiments, except that the experiments donít give a single answer. So, we need to run a series of experiments. Towards that goal, set up a spreadsheet in which to record the results of the experiments. Have a column of each experiment.
Task 7: Run 10 trials and record the three statistics in a spreadsheet. Figure the average of the total drops.
Inspect the numbers in the spreadsheet. The model seems to be generating many drops, and covering the area to a great depth both in terms of the maximum depth and average depth. It is difficult to believe with our idea of how water works that such high average depths are realistic in terms of getting the pavement wet. The model seems to be creating too many drops.
One problem is that the drops are not spreading out. Perhaps if they spread out, the tiny spaces between the drops that force the model to keep generating drops for so long would become covered up. This would be more realistic, but because our model is a "two dimensional" model, i.e the raindrops are not spherical when they "splat" on the pavement, they donít really "contain" any water. They just represent the flattened sphere. For this exercise, however, we will say that a drop spreads out so that its radius is 10% larger than its original value. The approach will be to keep for each drop the amount it should spread out. Then each time the drop is processed in the
check routine, the dropís radius will be increased by one if it has not completely spread out. This is to represent the idea that the spread occurs over time, not instantaneously.Task 8: Add a new integer array with 3000 elements to the
rainDrop program. When the ith drop is generated, the ith position of this variable is set to 10% of the rad(i) value. This variable must be passed as a parameter to the check procedure in its call in rainDrop. This also implies that the formal parameter list of the check procedure has to be changed to add a new formal parameter corresponding to it. Finally, within the loop of the check procedure, each drop is tested to see if its spread value has been reduced to zero. If it has, nothing happens. If it has not, then the spread value is reduced by 1 and the radius of this variable is increased by one.To see if this makes a difference, disable the Randomize call in Form_Load and test the program with and without the spread logic in the check procedure. Does it make a difference? Uncomment Randomize.
Task 9: Run 10 experiments with the spreading logic operational and gather the statistics on the runs. Include these on your speadsheet.
In general, has the spreading of the drops made a difference?
Task 10: Models of the physical world are only as good as the assumptions made in the formulation of the model and the processing used to implement the model. Write a paragraph discussing the reliability of the rainDrop procedureís model. What aspects of rain is ignored or overly simplified in the model?
It is amazing how difficult it is to make a computer do what raindrops manage to do with no effort!